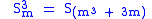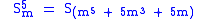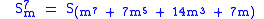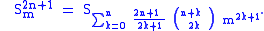
Silver ratio
Encyclopedia
| Binary Binary numeral system The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2... |
10.0110101000001001111... |
| Decimal Decimal The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations.... |
2.4142135623730950488... |
| Hexadecimal Hexadecimal In mathematics and computer science, hexadecimal is a positional numeral system with a radix, or base, of 16. It uses sixteen distinct symbols, most often the symbols 0–9 to represent values zero to nine, and A, B, C, D, E, F to represent values ten to fifteen... |
2.6A09E667F3BCC908B2F... |
| Continued fraction Continued fraction In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on... |
 |
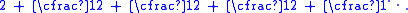| Algebraic form Algebraic number In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental... |
 |
In mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
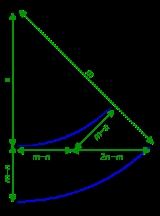
, two quantities are in the silver ratio if the ratio
Ratio
In mathematics, a ratio is a relationship between two numbers of the same kind , usually expressed as "a to b" or a:b, sometimes expressed arithmetically as a dimensionless quotient of the two which explicitly indicates how many times the first number contains the second In mathematics, a ratio is...
between the sum of the smaller plus twice the larger of those quantities and the larger one is the same as the ratio between the larger one and the smaller. This defines the silver ratio as an irrational
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
mathematical constant
Mathematical constant
A mathematical constant is a special number, usually a real number, that is "significantly interesting in some way". Constants arise in many different areas of mathematics, with constants such as and occurring in such diverse contexts as geometry, number theory and calculus.What it means for a...
, whose value of one plus the square root of 2
Square root of 2
The square root of 2, often known as root 2, is the positive algebraic number that, when multiplied by itself, gives the number 2. It is more precisely called the principal square root of 2, to distinguish it from the negative number with the same property.Geometrically the square root of 2 is the...
is approximately 2.4142135623. Its name is an allusion to the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
; analogously to the way the golden ratio is the limiting ratio of consecutive Fibonacci number
Fibonacci number
In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
s, the silver ratio is the limiting ratio of consecutive Pell number
Pell number
In mathematics, the Pell numbers are an infinite sequence of integers that have been known since ancient times, the denominators of the closest rational approximations to the square root of 2. This sequence of approximations begins 1/1, 3/2, 7/5, 17/12, and 41/29, so the sequence of Pell numbers...
s. The silver ratio is denoted by δS.
Mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
s have studied the silver ratio since the time of the Greeks (although perhaps without giving a special name until recently) because of its connections to the square root of 2
Square root of 2
The square root of 2, often known as root 2, is the positive algebraic number that, when multiplied by itself, gives the number 2. It is more precisely called the principal square root of 2, to distinguish it from the negative number with the same property.Geometrically the square root of 2 is the...
, its covergents, square triangular number
Square triangular number
In mathematics, a square triangular number is a number which is both a triangular number and a perfect square....
s, Pell number
Pell number
In mathematics, the Pell numbers are an infinite sequence of integers that have been known since ancient times, the denominators of the closest rational approximations to the square root of 2. This sequence of approximations begins 1/1, 3/2, 7/5, 17/12, and 41/29, so the sequence of Pell numbers...
s, octagons and the like.
The relation described above can be expressed algebraically:
The silver ratio can also be defined by the simple continued fraction
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
[2; 2, 2, 2, ...]:
The convergents
Convergent (continued fraction)
A convergent is one of a sequence of values obtained by evaluating successive truncations of a continued fraction The nth convergent is also known as the nth approximant of a continued fraction.-Representation of real numbers:...
of this continued fraction (2/1, 5/2, 12/5, 29/12, 70/29, ...) are ratios of consecutive Pell number
Pell number
In mathematics, the Pell numbers are an infinite sequence of integers that have been known since ancient times, the denominators of the closest rational approximations to the square root of 2. This sequence of approximations begins 1/1, 3/2, 7/5, 17/12, and 41/29, so the sequence of Pell numbers...
s. These fractions provide accurate rational approximations
Diophantine approximation
In number theory, the field of Diophantine approximation, named after Diophantus of Alexandria, deals with the approximation of real numbers by rational numbers....
of the silver ratio, analogous to the approximation of the golden ratio by ratios of consecutive Fibonacci number
Fibonacci number
In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
s.
Number-theoretic properties
The silver ratio is a Pisot–Vijayaraghavan number (PV number), as its conjugate has absolute value less than 1. In fact it's the second smallest quadratic PV number after the golden ratio. This means the distance from δ to the nearest integer is . Thus, the sequence of fractional partFractional part
All real numbers can be written in the form n + r where n is an integer and the remaining fractional part r is a nonnegative real number less than one...
s of δ, (taken as elements of the torus) converges. In particular, this sequence is not equidistributed mod 1.
Powers
The lower powers of the silver ratio are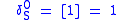
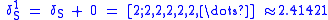
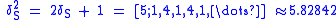
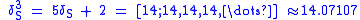
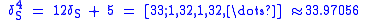
The powers continue in the pattern
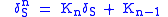
where
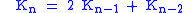
For example, using this property:
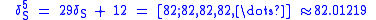
Using and as initial conditions, a Binet-like formula results from solving the recurrence relation
which becomes
Trigonometric properties
See Exact trigonometric constantsThe silver ratio is intimately connected to trigonometric ratios for .
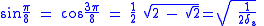
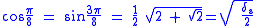
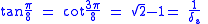
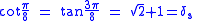
So the area of a regular octagon with side length a is given by
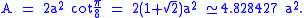
Silver means
| Silver means | ||
| 0: | ½ (0 + √4) | 1 |
| 1: | ½ (1 + √5) | 1.618033989 Golden ratio In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989... |
| 2: | ½ (2 + √8) | 2.414213562 |
| 3: | ½ (3 + √13) | 3.302775638 |
| 4: | ½ (4 + √20) | 4.236067978 |
| 5: | ½ (5 + √29) | 5.192582404 |
| 6: | ½ (6 + √40) | 6.162277660 |
| 7: | ½ (7 + √53) | 7.140054945 |
| 8: | ½ (8 + √68) | 8.123105626 |
| 9: | ½ (9 + √85) | 9.109772229 |
| ... | ||
| n: | ½ {n + √(n^2 + 4)} | |
The more general simple continued fraction
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
expressions
are known as the silver means or metallic means of the successive natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s. The golden ratio is the silver mean between 1 and 2, while the silver ratio is the silver mean between 2 and 3. The term "bronze ratio" and other metal names are occasionally coined for subsequent silver means. The values of the first ten silver means are shown at right. Notice that each silver mean is a root of the simple quadratic equation
where n is any positive natural number.
Properties
These properties are valid only for integers m, for nonintegers the properties are similar but slightly different.The above property for the powers of the silver ratio is a consequence of a property of the powers of silver means. For the silver mean S of m, the property can be generalized as
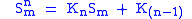
where
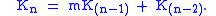
Using the initial conditions and , this recurrence relation becomes
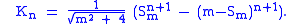
The powers of silver means have other interesting properties:
- If n is a positive even integer:
Additionally,
Also,
In general:
The silver mean S of m also has the property that
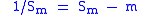
meaning that the inverse of a silver mean has the same decimal part as the corresponding silver mean.
where a is the integer part of S and b is the decimal part of S, then the following property is true:
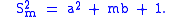
Because (for all m greater than 0), the integer part of , . For , we then have
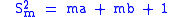
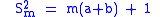
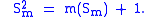
Therefore the silver mean of m is a solution of the equation
It may also be useful to note that the silver mean S of −m is the inverse of the silver mean S of m
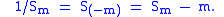
Another interesting result can be obtained by slightly changing the formula of the silver mean. If we consider a number
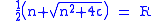
then the following properties are true:
if c is real,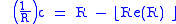
if c is a multiple of i.The silver mean of m is also given by the integral
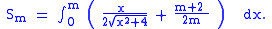
Paper sizes and silver rectangles
The paper sizePaper size
Many paper size standards conventions have existed at different times and in different countries. Today there is one widespread international ISO standard and a localised standard used in North America . The paper sizes affect writing paper, stationery, cards, and some printed documents...
s under ISO 216
ISO 216
ISO 216 specifies international standard paper sizes used in most countries in the world today. It defines the "A" and "B" series of paper sizes, including A4, the most commonly available size...
are rectangle
Rectangle
In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...
s in the proportion 1:√2 sometimes called "A4 rectangles". Removing a largest possible square from a sheet of such paper leaves a rectangle
Rectangle
In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...
with proportions 1:√2-1 which is the same as 1+√2:1 , the silver ratio. Removing a largest square from one of these sheets leaves one again with aspect ratio √2. A rectangle whose aspect ratio is the silver ratio is sometimes called a silver rectangle by analogy with golden rectangles. Confusingly, "silver rectangle" can also refer to the paper sizes specified by ISO 216
ISO 216
ISO 216 specifies international standard paper sizes used in most countries in the world today. It defines the "A" and "B" series of paper sizes, including A4, the most commonly available size...
.
However, only the Lichtenberg ratio
Lichtenberg ratio
In paper sizes, the Lichtenberg ratio is the aspect ratio of 1:√2. The term was proposed by Markus Kuhn in 2002.This aspect ratio has the unique property that cutting any rectangular sheet of paper formed with the Lichtenberg ratio into two equal halves parallel to its shortest sides produces two...
rectangles (rectangles with the shape of ISO 216 paper) have the property that by cutting the rectangle in half across its long side produces two smaller rectangles of the same aspect ratio.
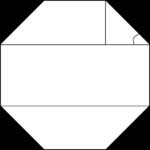
The silver rectangle is connected to the regular octagon. If a regular octagon is partitioned into two isosceles trapezoids and a rectangle, then the rectangle is a silver rectangle with an aspect ratio of 1:δS, and the 4 sides of the trapezoids are in a ratio of 1:1:1:δS.
If the edge length of a regular octagon is t, then the inradius of the octagon (the distance between opposite sides) is δSt, and the area of the octagon is 2δSt2.