Diophantine approximation
Encyclopedia
In number theory
, the field of Diophantine approximation, named after Diophantus of Alexandria, deals with the approximation of real number
s by rational number
s.
The absolute value of the difference between the real number to be approximated and the rational number that approximates it is a crude measure of how good the approximation is. However, since the rational numbers are dense in the real numbers, one can always find rational numbers that are arbitrarily close to the number being approximated. So this measure tells us nothing about the "quality" of the approximation.
A better measure of the quality of the approximation is by comparison of the difference to the size of the denominator.
E.g., 22/7 and 179/57 are roughly equally far from π, but number theorists would consider 22/7 to be a better approximation because its denominator is smaller.
s, as applied to square root
s of integers and other quadratic irrationals, was studied from a diophantine point-of-view by Fermat, Euler and others.
In the 1840s, Joseph Liouville
obtained an important result on general algebraic number
s (the Lemma on the page for Liouville number). If x is an irrational algebraic number of degree n over the rational numbers, then there exists a constant such that
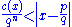
holds for all integers p and q where .
This result allowed him to produce the first proven examples of transcendental numbers. This link between diophantine approximation and transcendence theory
continues to the present-day. Many of the proof techniques are shared between the two areas.
Liouville's result was improved by Axel Thue
and others, leading in the end to a definitive theorem of Roth
: the exponent in the theorem was reduced from n, the degree of the algebraic number, to any number greater than 2 (e.g. 2 + ε). Subsequently, Wolfgang M. Schmidt
generalised this to the case of simultaneous approximation. The proofs were difficult, and not effective
. This means that we cannot use the results or their proofs to obtain bounds on the size of solutions of associated diophantine equations. However, the techniques and results can often be used to bound the number of solutions of such equations.
Note that Khinchine proved that if
is a non-increasing function and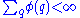
, then for almost all real numbers x (not necessarily algebraic), there are at most finitely many rational p/q with q not zero and
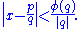
Similarly, if the sum diverges, then for almost all real numbers, there are infinitely many such rational numbers p/q.
In 1941, R.J. Duffin and A.C. Schaeffer proved a more general theorem that implies Khinchine's result, and made a conjecture now known by their name as the Duffin–Schaeffer conjecture. In 2006, V. Beresnevich and S. Velani proved a Hausdorff measure analogue of the conjecture, published in the Annals of Mathematics
.
There are several effective techniques and results available. The most general is lower bounds for linear forms in logarithms
, which were developed by Alan Baker. A refinement of Baker's theorem
by Fel'dman implied that if x is an algebraic number of degree n over the rational numbers, then there exist effectively computable constants c(x) > 0 and 0 < d(x) < n such that
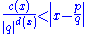
holds for all rational integers with q not zero.
, which is a circle. For any interval I on the circle we look at the proportion of the sequence's elements that lie in it, up to some integer N, and compare it to the proportion of the circumference occupied by I. Uniform distribution means that in the limit, as N grows, the proportion of hits on the interval tends to the 'expected' value. Hermann Weyl
proved a basic result showing that this was equivalent to bounds for exponential sums formed from the sequence. This showed that Diophantine approximation results were closely related to the general problem of cancellation in exponential sums, which occurs throughout analytic number theory
in the bounding of error terms.
Related to uniform distribution is the topic of irregularities of distribution, which is of a combinatorial
nature.
outlined a broad program rooted in ergodic theory
that allows one to prove number-theoretic results using the dynamical and ergodic properties of actions of subgroups of semisimple Lie groups. The work of D.Kleinbock, G.Margulis, and their collaborators demonstrated the power of this novel approach to classical problems in Diophantine approximation. Among its notable successes are the proof of the decades-old Oppenheim conjecture
by Margulis, with later extensions by Dani and Margulis and Eskin–Margulis–Mozes, and the proof of Baker and Sprindzhuk conjectures in the Diophantine approximations on manifolds by Kleinbock and Margulis. Various generalizations of the above results of Aleksandr Khinchin in metric Diophantine approximation have also been obtained within this framework.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the field of Diophantine approximation, named after Diophantus of Alexandria, deals with the approximation of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s by rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s.
The absolute value of the difference between the real number to be approximated and the rational number that approximates it is a crude measure of how good the approximation is. However, since the rational numbers are dense in the real numbers, one can always find rational numbers that are arbitrarily close to the number being approximated. So this measure tells us nothing about the "quality" of the approximation.
A better measure of the quality of the approximation is by comparison of the difference to the size of the denominator.
E.g., 22/7 and 179/57 are roughly equally far from π, but number theorists would consider 22/7 to be a better approximation because its denominator is smaller.
Approximation to algebraic numbers
The theory of continued fractionContinued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
s, as applied to square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
s of integers and other quadratic irrationals, was studied from a diophantine point-of-view by Fermat, Euler and others.
In the 1840s, Joseph Liouville
Joseph Liouville
- Life and work :Liouville graduated from the École Polytechnique in 1827. After some years as an assistant at various institutions including the Ecole Centrale Paris, he was appointed as professor at the École Polytechnique in 1838...
obtained an important result on general algebraic number
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s (the Lemma on the page for Liouville number). If x is an irrational algebraic number of degree n over the rational numbers, then there exists a constant such that
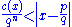
holds for all integers p and q where .
This result allowed him to produce the first proven examples of transcendental numbers. This link between diophantine approximation and transcendence theory
Transcendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
continues to the present-day. Many of the proof techniques are shared between the two areas.
Liouville's result was improved by Axel Thue
Axel Thue
Axel Thue was a Norwegian mathematician, known for highly original work in diophantine approximation, and combinatorics....
and others, leading in the end to a definitive theorem of Roth
Thue–Siegel–Roth theorem
In mathematics, the Thue–Siegel–Roth theorem, also known simply as Roth's theorem, is a foundational result in diophantine approximation to algebraic numbers. It is of a qualitative type, stating that a given algebraic number α may not have too many rational number approximations, that are 'very...
: the exponent in the theorem was reduced from n, the degree of the algebraic number, to any number greater than 2 (e.g. 2 + ε). Subsequently, Wolfgang M. Schmidt
Wolfgang M. Schmidt
Wolfgang M. Schmidt is a mathematician born in 1933. He studied mathematics at the University of Vienna, where he received his PhD, which was supervised by Edmund Hlawka, in 1955...
generalised this to the case of simultaneous approximation. The proofs were difficult, and not effective
Effective results in number theory
For historical reasons and in order to have application to the solution of Diophantine equations, results in number theory have been scrutinised more than in other branches of mathematics to see if their content is effectively computable...
. This means that we cannot use the results or their proofs to obtain bounds on the size of solutions of associated diophantine equations. However, the techniques and results can often be used to bound the number of solutions of such equations.
Note that Khinchine proved that if
is a non-increasing function and
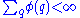, then for almost all real numbers x (not necessarily algebraic), there are at most finitely many rational p/q with q not zero and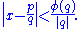Similarly, if the sum diverges, then for almost all real numbers, there are infinitely many such rational numbers p/q.
In 1941, R.J. Duffin and A.C. Schaeffer proved a more general theorem that implies Khinchine's result, and made a conjecture now known by their name as the Duffin–Schaeffer conjecture. In 2006, V. Beresnevich and S. Velani proved a Hausdorff measure analogue of the conjecture, published in the Annals of Mathematics
Annals of Mathematics
The Annals of Mathematics is a bimonthly mathematical journal published by Princeton University and the Institute for Advanced Study. It ranks amongst the most prestigious mathematics journals in the world by criteria such as impact factor.-History:The journal began as The Analyst in 1874 and was...
.
There are several effective techniques and results available. The most general is lower bounds for linear forms in logarithms
Linear forms in logarithms
In number theory the method of linear forms in logarithms is the application of estimatesfor the magnitude of a finite sum\sum \beta_i\log\alpha_i=\Lambda,...
, which were developed by Alan Baker. A refinement of Baker's theorem
Baker's theorem
In transcendence theory, a mathematical discipline, Baker's theorem gives a lower bound for linear combinations of logarithms of algebraic numbers...
by Fel'dman implied that if x is an algebraic number of degree n over the rational numbers, then there exist effectively computable constants c(x) > 0 and 0 < d(x) < n such that
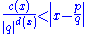
holds for all rational integers with q not zero.
Uniform distribution
Another topic that has seen a thorough development is the theory of uniform distribution mod 1. Take a sequence a1, a2, ... of real numbers and consider their fractional parts. That is, more abstractly, look at the sequence in R/ZQuotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
, which is a circle. For any interval I on the circle we look at the proportion of the sequence's elements that lie in it, up to some integer N, and compare it to the proportion of the circumference occupied by I. Uniform distribution means that in the limit, as N grows, the proportion of hits on the interval tends to the 'expected' value. Hermann Weyl
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
proved a basic result showing that this was equivalent to bounds for exponential sums formed from the sequence. This showed that Diophantine approximation results were closely related to the general problem of cancellation in exponential sums, which occurs throughout analytic number theory
Analytic number theory
In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Dirichlet's introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic...
in the bounding of error terms.
Related to uniform distribution is the topic of irregularities of distribution, which is of a combinatorial
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
nature.
Unsolved problems
There are still simply-stated unsolved problems remaining in Diophantine approximation, for example the Littlewood conjecture.Recent developments
In his plenary address at the International Mathematical Congress in Kyoto (1990), Grigory MargulisGrigory Margulis
Gregori Aleksandrovich Margulis is a Russian mathematician known for his far-reaching work on lattices in Lie groups, and the introduction of methods from ergodic theory into diophantine approximation. He was awarded a Fields Medal in 1978 and a Wolf Prize in Mathematics in 2005, becoming the...
outlined a broad program rooted in ergodic theory
Ergodic theory
Ergodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics....
that allows one to prove number-theoretic results using the dynamical and ergodic properties of actions of subgroups of semisimple Lie groups. The work of D.Kleinbock, G.Margulis, and their collaborators demonstrated the power of this novel approach to classical problems in Diophantine approximation. Among its notable successes are the proof of the decades-old Oppenheim conjecture
Oppenheim conjecture
In Diophantine approximation, the Oppenheim conjecture concerns representations of numbers by real quadratic forms in several variables. It was formulated in 1929 by Alexander Oppenheim and later the conjectured property was further strengthened by Davenport and Oppenheim...
by Margulis, with later extensions by Dani and Margulis and Eskin–Margulis–Mozes, and the proof of Baker and Sprindzhuk conjectures in the Diophantine approximations on manifolds by Kleinbock and Margulis. Various generalizations of the above results of Aleksandr Khinchin in metric Diophantine approximation have also been obtained within this framework.
External links
- Diophantine Approximation: historical survey. From Introduction to Diophantine methods course by Michel Waldschmidt.