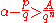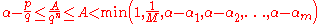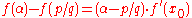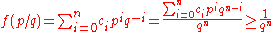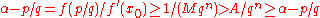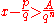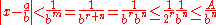Liouville number
Encyclopedia
In number theory
, a Liouville number is a real number
x with the property that, for every positive integer
n, there exist integers p and q with q > 1 and such that
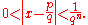
A Liouville number can thus be approximated "quite closely" by a sequence
of rational numbers. In 1844, Joseph Liouville
showed that all Liouville numbers are transcendental
, thus establishing the existence of transcendental numbers for the first time.
It is relatively easily proven that if x is a Liouville number, x is irrational
. Assume otherwise; then there exist integers c, d with d > 0 and x = c/d. Let n be a positive integer such that 2n − 1 > d. Then if p and q are any integers such that q > 1 and p/q ≠ c/d, then
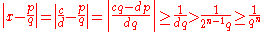
which contradicts the definition of Liouville number.
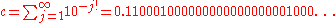
is known as Liouville's constant. Liouville's constant is a Liouville number; if we define pn and qn as follows:
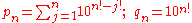
then we have for all positive integers n
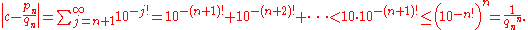
3.14(3 zeros)1(17 zeros)5(95 zeros)9(599 zeros)2...
where the digits are zero except in positions n! where the digit equals the nth digit following the decimal point in the decimal expansion of π.
This number, as well as any other non-terminating decimal with its non-zero digits similarly situated, satisfies the definition of Liouville number. Since the set of all sequences of non-null digits has the cardinality of the continuum
, the same thing occurs with the set of all Liouville numbers. Moreover, the Liouville numbers form a dense
subset of the set of real numbers.
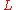is small. More precisely, its Lebesgue measure
is zero. The proof given follows some ideas by John C. Oxtoby.
For positive integers
and 
set: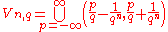
– we have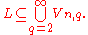 
Observe that for each positive integer
and 
, we also have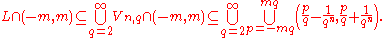
Since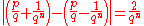
and 
we have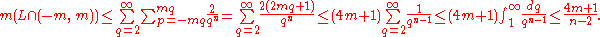
Now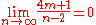
and it follows that for each positive integer 
, 
has Lebesgue measure zero. Consequently, so has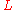 
.
In contrast, the Lebesgue measure of the set
of all real transcendental numbers is infinite (since 
is the complement of a null set).
In fact, the Hausdorff dimension
of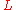
is zero, which implies that the Hausdorff measure
of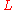
is zero for all dimension 
. Hausdorff dimension of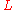 
under other dimension functions has also been investigated.
.
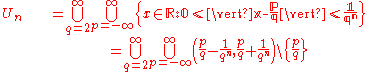The set of all Liouville numbers can thus be written as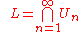
.
Each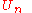
is an open set
; as its closure contains all rationals (the {p/q}'s from each punctured interval), it is also a dense
subset of real line. Since it is the intersection of countably many such open dense sets,
is comeagre
, that is to say, it is a dense Gδ
set.
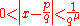
is satisfied by an infinite number of integer pairs (p, q) with q > 0. This least upper bound is defined to be the irrationality measure of x. For any value μ less than this upper bound, the infinite set of all rationals p/q satisfying the above inequality yield an approximation of x. Conversely, if μ is greater than the upper bound, then there are at most finitely many (p, q) with q > 0 that satisfy the inequality; thus, the opposite inequality holds for all larger values of q. In other words, given the irrationality measure μ of a real number x, whenever a rational approximation x ≅ p/q, p,q ∈ N yields n + 1 exact decimal digits, we have
except for at most a finite number of “lucky” pairs (p, q).
For a rational number α the irrationality measure is μ(α) = 1.
The Thue–Siegel–Roth theorem
proves that if α is an algebraic number
, real but not rational, it is μ(α) = 2.
Transcendental numbers have irrationality measure 2 or greater. As an example, e
has μ(e) = 2 even though e is transcendental.
The Liouville numbers are precisely those numbers having infinite irrationality measure.
, as will be proven below. Establishing that a given number is a Liouville number provides a useful tool for proving a given number is transcendental. Unfortunately, not every transcendental number is a Liouville number. The terms in the continued fraction
expansion of every Liouville number are unbounded; using a counting argument, one can then show that there must be uncountably many transcendental numbers which are not Liouville. Using the explicit continued fraction expansion of e
, one can show that e is an example of a transcendental number that is not Liouville. Mahler proved in 1953 that π
is another such example.
The proof proceeds by first establishing a property of irrational
algebraic number
s. This property essentially says that irrational algebraic numbers cannot be well approximated by rational numbers. A Liouville number is irrational but does not have this property, so it can't be algebraic and must be transcendental. The following lemma
is usually known as Liouville's theorem (on diophantine approximation), there being several results known as Liouville's theorem
.
Lemma: If α is an irrational number which is the root of a polynomial
f of degree
n > 0 with integer coefficients, then there exists a real number A > 0 such that, for all integers p, q, with q > 0,
Proof of Lemma: Let M be the maximum value of |f ′(x)| (the absolute value
of the derivative
of f) over the interval
[α − 1, α + 1]. Let α1, α2, ..., αm be the distinct roots of f which differ from α. Select some value A > 0 satisfying
Now assume that there exists some integers p, q contradicting the lemma. Then
Then p/q is in the interval [α − 1, α + 1]; and p/q is not in {α1, α2, ..., αm}, so p/q is not a root of f; and there is no root of f between α and p/q.
By the mean value theorem
, there exists an x0 between p/q and α such that
Since α is a root of f but p/q is not, we see that |f ′(x0)| > 0 and we can rearrange:
Now, f is of the form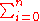
ci xi where each ci is an integer; so we can express |f(p/q)| as
the last inequality holding because p/q is not a root of f and the ci are integers.
Thus we have that |f(p/q)| ≥ 1/qn. Since |f ′(x0)| ≤ M by the definition of M, and 1/M > A by the definition of A, we have that
which is a contradiction; therefore, no such p, q exist; proving the lemma.
Proof of assertion: As a consequence of this lemma, let x be a Liouville number; as noted in the article text, x is then irrational. If x is algebraic, then by the lemma, there exists some integer n and some positive real A such that for all p, q
Let r be a positive integer such that 1/(2r) ≤ A. If we let m = r + n, then, since x is a Liouville number, there exists integers a, b > 1 such that
which contradicts the lemma; therefore x is not algebraic, and is thus transcendental.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, a Liouville number is a real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
x with the property that, for every positive integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
n, there exist integers p and q with q > 1 and such that
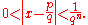
A Liouville number can thus be approximated "quite closely" by a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of rational numbers. In 1844, Joseph Liouville
Joseph Liouville
- Life and work :Liouville graduated from the École Polytechnique in 1827. After some years as an assistant at various institutions including the Ecole Centrale Paris, he was appointed as professor at the École Polytechnique in 1838...
showed that all Liouville numbers are transcendental
Transcendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
, thus establishing the existence of transcendental numbers for the first time.
Elementary properties
An equivalent definition to the one given above is that for any positive integer n, there exists an infinite number of pairs of integers (p,q) obeying the above inequality.It is relatively easily proven that if x is a Liouville number, x is irrational
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
. Assume otherwise; then there exist integers c, d with d > 0 and x = c/d. Let n be a positive integer such that 2n − 1 > d. Then if p and q are any integers such that q > 1 and p/q ≠ c/d, then
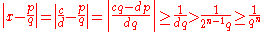
which contradicts the definition of Liouville number.
Liouville constant
The number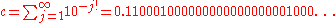is known as Liouville's constant. Liouville's constant is a Liouville number; if we define pn and qn as follows:
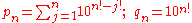
then we have for all positive integers n
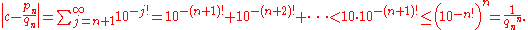
Uncountability
Consider, for example, the number- 3.1400010000000000000000050000....
3.14(3 zeros)1(17 zeros)5(95 zeros)9(599 zeros)2...
where the digits are zero except in positions n! where the digit equals the nth digit following the decimal point in the decimal expansion of π.
This number, as well as any other non-terminating decimal with its non-zero digits similarly situated, satisfies the definition of Liouville number. Since the set of all sequences of non-null digits has the cardinality of the continuum
Cardinality of the continuum
In set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....
, the same thing occurs with the set of all Liouville numbers. Moreover, the Liouville numbers form a dense
Dense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
subset of the set of real numbers.
Liouville numbers and measure
From the point of view of measure theory, the set of all Liouville numbers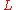 is small. More precisely, its Lebesgue measureLebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
is zero. The proof given follows some ideas by John C. Oxtoby.
For positive integers
and set: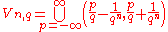 – we have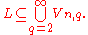 Observe that for each positive integer
and , we also have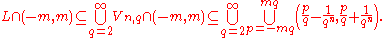Since
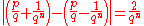and we have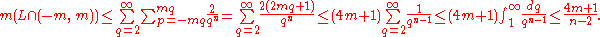Now
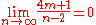and it follows that for each positive integer , has Lebesgue measure zero. Consequently, so has 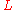.In contrast, the Lebesgue measure of the set
of all real transcendental numbers is infinite (since is the complement of a null set).In fact, the Hausdorff dimension
Hausdorff dimension
thumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...
of
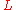is zero, which implies that the Hausdorff measureHausdorff measure
In mathematics a Hausdorff measure is a type of outer measure, named for Felix Hausdorff, that assigns a number in [0,∞] to each set in Rn or, more generally, in any metric space. The zero dimensional Hausdorff measure is the number of points in the set or ∞ if the set is infinite...
of
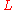is zero for all dimension . Hausdorff dimension of 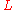under other dimension functions has also been investigated.Liouville numbers and topology
For each positive integer n, set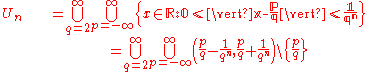.The set of all Liouville numbers can thus be written as
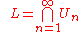.Each
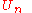is an open setOpen set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
; as its closure contains all rationals (the {p/q}'s from each punctured interval), it is also a dense
Dense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
subset of real line. Since it is the intersection of countably many such open dense sets,
is comeagreMeagre set
In the mathematical fields of general topology and descriptive set theory, a meagre set is a set that, considered as a subset of a topological space, is in a precise sense small or negligible...
, that is to say, it is a dense Gδ
G-delta set
In the mathematical field of topology, a Gδ set is a subset of a topological space that is a countable intersection of open sets. The notation originated in Germany with G for Gebiet meaning open set in this case and δ for Durchschnitt .The term inner limiting set is also used...
set.
Irrationality measure
The irrationality measure (or approximation exponent or Liouville–Roth constant) of a real number x is a measure of how "closely" it can be approximated by rationals. Generalizing the definition of Liouville numbers, instead of allowing any n in the power of q, we find the least upper bound of the set of real numbers μ such that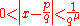is satisfied by an infinite number of integer pairs (p, q) with q > 0. This least upper bound is defined to be the irrationality measure of x. For any value μ less than this upper bound, the infinite set of all rationals p/q satisfying the above inequality yield an approximation of x. Conversely, if μ is greater than the upper bound, then there are at most finitely many (p, q) with q > 0 that satisfy the inequality; thus, the opposite inequality holds for all larger values of q. In other words, given the irrationality measure μ of a real number x, whenever a rational approximation x ≅ p/q, p,q ∈ N yields n + 1 exact decimal digits, we have
except for at most a finite number of “lucky” pairs (p, q).
For a rational number α the irrationality measure is μ(α) = 1.
The Thue–Siegel–Roth theorem
Thue–Siegel–Roth theorem
In mathematics, the Thue–Siegel–Roth theorem, also known simply as Roth's theorem, is a foundational result in diophantine approximation to algebraic numbers. It is of a qualitative type, stating that a given algebraic number α may not have too many rational number approximations, that are 'very...
proves that if α is an algebraic number
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
, real but not rational, it is μ(α) = 2.
Transcendental numbers have irrationality measure 2 or greater. As an example, e
E (mathematical constant)
The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
has μ(e) = 2 even though e is transcendental.
The Liouville numbers are precisely those numbers having infinite irrationality measure.
Liouville numbers and transcendence
All Liouville numbers are transcendentalTranscendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
, as will be proven below. Establishing that a given number is a Liouville number provides a useful tool for proving a given number is transcendental. Unfortunately, not every transcendental number is a Liouville number. The terms in the continued fraction
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
expansion of every Liouville number are unbounded; using a counting argument, one can then show that there must be uncountably many transcendental numbers which are not Liouville. Using the explicit continued fraction expansion of e
E (mathematical constant)
The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
, one can show that e is an example of a transcendental number that is not Liouville. Mahler proved in 1953 that π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
is another such example.
The proof proceeds by first establishing a property of irrational
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
algebraic number
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s. This property essentially says that irrational algebraic numbers cannot be well approximated by rational numbers. A Liouville number is irrational but does not have this property, so it can't be algebraic and must be transcendental. The following lemma
Lemma (mathematics)
In mathematics, a lemma is a proven proposition which is used as a stepping stone to a larger result rather than as a statement in-and-of itself...
is usually known as Liouville's theorem (on diophantine approximation), there being several results known as Liouville's theorem
Liouville's theorem
Liouville's theorem has various meanings, all mathematical results named after Joseph Liouville:*In complex analysis, see Liouville's theorem ; there is also a related theorem on harmonic functions....
.
Lemma: If α is an irrational number which is the root of a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
f of degree
Degree (mathematics)
In mathematics, there are several meanings of degree depending on the subject.- Unit of angle :A degree , usually denoted by ° , is a measurement of a plane angle, representing 1⁄360 of a turn...
n > 0 with integer coefficients, then there exists a real number A > 0 such that, for all integers p, q, with q > 0,
Proof of Lemma: Let M be the maximum value of |f ′(x)| (the absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of f) over the interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
[α − 1, α + 1]. Let α1, α2, ..., αm be the distinct roots of f which differ from α. Select some value A > 0 satisfying
Now assume that there exists some integers p, q contradicting the lemma. Then
Then p/q is in the interval [α − 1, α + 1]; and p/q is not in {α1, α2, ..., αm}, so p/q is not a root of f; and there is no root of f between α and p/q.
By the mean value theorem
Mean value theorem
In calculus, the mean value theorem states, roughly, that given an arc of a differentiable curve, there is at least one point on that arc at which the derivative of the curve is equal to the "average" derivative of the arc. Briefly, a suitable infinitesimal element of the arc is parallel to the...
, there exists an x0 between p/q and α such that
Since α is a root of f but p/q is not, we see that |f ′(x0)| > 0 and we can rearrange:
Now, f is of the form
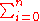ci xi where each ci is an integer; so we can express |f(p/q)| as
the last inequality holding because p/q is not a root of f and the ci are integers.
Thus we have that |f(p/q)| ≥ 1/qn. Since |f ′(x0)| ≤ M by the definition of M, and 1/M > A by the definition of A, we have that
which is a contradiction; therefore, no such p, q exist; proving the lemma.
Proof of assertion: As a consequence of this lemma, let x be a Liouville number; as noted in the article text, x is then irrational. If x is algebraic, then by the lemma, there exists some integer n and some positive real A such that for all p, q
Let r be a positive integer such that 1/(2r) ≤ A. If we let m = r + n, then, since x is a Liouville number, there exists integers a, b > 1 such that
which contradicts the lemma; therefore x is not algebraic, and is thus transcendental.