A Kepler triangle is a right triangle with edge lengths in geometric progression

Geometric progression

In mathematics, a geometric progression, also known as a geometric sequence, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed non-zero number called the common ratio. For example, the sequence 2, 6, 18, 54, ... is a geometric progression...

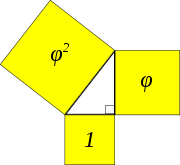
. The ratio of the edges of a Kepler triangle are linked to the golden ratio

Golden ratio

In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...

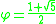
and can be written: 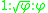, or approximately 1 : 1.272 : 1.618. The squares of the edges of this triangle (see figure) are in geometric progression

Geometric progression

In mathematics, a geometric progression, also known as a geometric sequence, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed non-zero number called the common ratio. For example, the sequence 2, 6, 18, 54, ... is a geometric progression...

 according to the golden ratio

Golden ratio

In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...

.

Triangles with such ratios are named after the German mathematician

Mathematician

A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....

 and astronomer

Astronomer

An astronomer is a scientist who studies celestial bodies such as planets, stars and galaxies.Historically, astronomy was more concerned with the classification and description of phenomena in the sky, while astrophysics attempted to explain these phenomena and the differences between them using...

 Johannes Kepler

Johannes Kepler

Johannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...

(1571–1630), who first demonstrated that this triangle is characterised by a ratio between short side and hypotenuse equal to the golden ratio. Kepler triangles combine two key mathematical concepts—the Pythagorean theorem

Pythagorean theorem

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...

 and the golden ratio

Golden ratio

In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...

—that fascinated Kepler deeply, as he expressed in this quotation:
Some sources claim that a triangle with dimensions closely approximating a Kepler triangle can be recognized in the Great Pyramid of Giza

Great Pyramid of Giza

The Great Pyramid of Giza is the oldest and largest of the three pyramids in the Giza Necropolis bordering what is now El Giza, Egypt. It is the oldest of the Seven Wonders of the Ancient World, and the only one to remain largely intact...

.

Derivation

The fact that a triangle with edges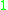 , and 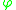, forms a right triangle follows directly from rewriting the defining quadratic polynomial for the golden ratio :


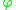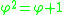
into the form of the Pythagorean theorem

Pythagorean theorem

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...

:

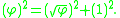
Relation to arithmetic, geometric, and harmonic mean

For positive real numbers a and b, their arithmetic mean

Arithmetic mean

In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...

, geometric mean

Geometric mean

The geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, except that the numbers are multiplied and then the nth root of the resulting product is taken.For instance, the...

, and harmonic mean

Harmonic mean

In mathematics, the harmonic mean is one of several kinds of average. Typically, it is appropriate for situations when the average of rates is desired....

 are the lengths of the sides of a right triangle if and only if that triangle is a Kepler triangle.

Constructing a Kepler triangle

A Kepler triangle can be constructed with only straightedge and compass by first creating a golden rectangle:

1. Construct a simple square
2. Draw a line from the midpoint of one side of the square to an opposite corner
3. Use that line as the radius to draw an arc that defines the height of the rectangle
4. Complete the golden rectangle
5. Use the longer side of the golden rectangle to draw an arc that intersects the opposite side of the rectangle and defines the hypotenuse
   Hypotenuse
   In geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse of a right triangle can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the...
   
    of the Kepler triangle

Kepler constructed it differently. In a letter to his former professor Michael Mästlin, he wrote, "If on a line which is divided in extreme and mean ratio one constructs a right angled triangle, such that the right angle is on the perpendicular put at the section point, then the smaller leg will equal the larger segment of the divided line."

A mathematical coincidence

Take any Kepler triangle with sides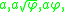 and consider:

• the circle that circumscribes it, and
• a square with side equal to the middle-sized edge of the triangle.

Then the perimeter

Perimeter

A perimeter is a path that surrounds an area. The word comes from the Greek peri and meter . The term may be used either for the path or its length - it can be thought of as the length of the outline of a shape. The perimeter of a circular area is called circumference.- Practical uses :Calculating...

s of the square () and the circle (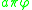) coincide up to an error less than 0.1%.

This is the mathematical coincidence 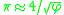. The square and the circle cannot have exactly the same perimeter, because in that case one would be able to solve the classical (impossible) problem of the quadrature of the circle

Squaring the circle

Squaring the circle is a problem proposed by ancient geometers. It is the challenge of constructing a square with the same area as a given circle by using only a finite number of steps with compass and straightedge...

. In other words, 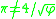because is a transcendental number

Transcendental number

In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...

.

According to some sources, Kepler triangles appear in the design of Egyptian pyramids, but the ancient Egyptians probably didn't know the mathematical coincidence involving the number and the golden ratio 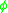.