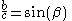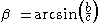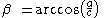Hypotenuse
Encyclopedia
In geometry
, a hypotenuse is the longest side of a right-angled triangle
, the side opposite the right angle
. The length of the hypotenuse of a right triangle
can be found using the Pythagorean theorem
, which states that the square of the length of the hypotenuse equals the sum of the squares of the lengths of the other two sides.
For example, if one of the other sides has a length of 3 meters (when squared, 9 m²) and the other has a length of 4 m (when squared, 16 m²), then their squares add up to 25 m². The length of the hypotenuse is the square root
of this, or 5 m.
hypotēnūsa, a transliteration of Ancient Greek
, the feminine
present
participle
of hypoteínō, a combination of hypó ("under") and teínō ("I stretch"). The word ὑποτείνουσα was used for the hypotenuse of a triangle by Plato in the Timeus 54d and by many other ancient authors.
A folk etymology says that tenuse means "side", so hypotenuse means a support like a prop or buttress
, but this is inaccurate.
Usually the length of the hypotenuse is calculated using the square root
function derived from the Pythagorean theorem
. Setting x = c1 and y = c2 to avoid subscripts:
In mathematical notation;
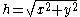
Many computer languages support the ISO C standard function hypot(x,y), which returns the value above. The function is designed not to fail where the straightforward calculation might overflow or underflow and can be slightly more accurate.
Some scientific calculators provide a function to convert from rectangular coordinates to polar coordinates. This gives both the length of the hypotenuse and the angle
the hypotenuse makes with the base line (c1 above) at the same time when given x and y. The angle returned will normally be that given by atan2
(y,x).
s:
, one can obtain the value of two acute angles,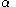
and 
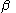, of the right triangle.
Given the length of the hypotenuse
and of a cathetus 
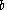, the ratio is:
The trigonometric inverse function is:
in which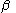
is the angle opposite the cathetus 
.
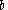The adjacent angle of the catheti
, will be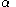 
= 90º –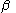 
One may also obtain the value of the angle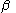
by the equation:
in which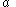
is the other cathetus.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a hypotenuse is the longest side of a right-angled triangle
Right triangle
A right triangle or right-angled triangle is a triangle in which one angle is a right angle . The relation between the sides and angles of a right triangle is the basis for trigonometry.-Terminology:The side opposite the right angle is called the hypotenuse...
, the side opposite the right angle
Right angle
In geometry and trigonometry, a right angle is an angle that bisects the angle formed by two halves of a straight line. More precisely, if a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles...
. The length of the hypotenuse of a right triangle
Right triangle
A right triangle or right-angled triangle is a triangle in which one angle is a right angle . The relation between the sides and angles of a right triangle is the basis for trigonometry.-Terminology:The side opposite the right angle is called the hypotenuse...
can be found using the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
, which states that the square of the length of the hypotenuse equals the sum of the squares of the lengths of the other two sides.
For example, if one of the other sides has a length of 3 meters (when squared, 9 m²) and the other has a length of 4 m (when squared, 16 m²), then their squares add up to 25 m². The length of the hypotenuse is the square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
of this, or 5 m.
Etymology
The word hypotenuse derives from LatinLatin
Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
hypotēnūsa, a transliteration of Ancient Greek
Ancient Greek
Ancient Greek is the stage of the Greek language in the periods spanning the times c. 9th–6th centuries BC, , c. 5th–4th centuries BC , and the c. 3rd century BC – 6th century AD of ancient Greece and the ancient world; being predated in the 2nd millennium BC by Mycenaean Greek...
, the feminine
Grammatical gender
Grammatical gender is defined linguistically as a system of classes of nouns which trigger specific types of inflections in associated words, such as adjectives, verbs and others. For a system of noun classes to be a gender system, every noun must belong to one of the classes and there should be...
present
Present tense
The present tense is a grammatical tense that locates a situation or event in present time. This linguistic definition refers to a concept that indicates a feature of the meaning of a verb...
participle
Participle
In linguistics, a participle is a word that shares some characteristics of both verbs and adjectives. It can be used in compound verb tenses or voices , or as a modifier...
of hypoteínō, a combination of hypó ("under") and teínō ("I stretch"). The word ὑποτείνουσα was used for the hypotenuse of a triangle by Plato in the Timeus 54d and by many other ancient authors.
A folk etymology says that tenuse means "side", so hypotenuse means a support like a prop or buttress
Buttress
A buttress is an architectural structure built against or projecting from a wall which serves to support or reinforce the wall...
, but this is inaccurate.
Calculating the hypotenuse
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
function derived from the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
. Setting x = c1 and y = c2 to avoid subscripts:
In mathematical notation;
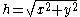
Many computer languages support the ISO C standard function hypot(x,y), which returns the value above. The function is designed not to fail where the straightforward calculation might overflow or underflow and can be slightly more accurate.
Some scientific calculators provide a function to convert from rectangular coordinates to polar coordinates. This gives both the length of the hypotenuse and the angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
the hypotenuse makes with the base line (c1 above) at the same time when given x and y. The angle returned will normally be that given by atan2
Atan2
In trigonometry, the two-argument function atan2 is a variation of the arctangent function. For any real arguments and not both equal to zero, is the angle in radians between the positive -axis of a plane and the point given by the coordinates on it...
(y,x).
Properties
Orthographic projectionOrthographic projection
Orthographic projection is a means of representing a three-dimensional object in two dimensions. It is a form of parallel projection, where all the projection lines are orthogonal to the projection plane, resulting in every plane of the scene appearing in affine transformation on the viewing surface...
s:
- The length of the hypotenuse equals the sum of the lengths of the orthographic projections of both catheti.
- The square of the length of a cathetus equals the productProduct (mathematics)In mathematics, a product is the result of multiplying, or an expression that identifies factors to be multiplied. The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the commutative law of multiplication...
of the lengths of its orthographic projection on the hypotenuse times the length of this.
-
- b² = a · m
- c² = a · n
- Also, the length of a cathetus b is the proportional mean between the lengths of its projection m and the hypotenuse a.
-
- a/b = b/m
- a/c = c/n
Trigonometric ratios
By means of trigonometric ratiosTrigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
, one can obtain the value of two acute angles,
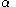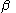and , of the right triangle.Given the length of the hypotenuse
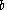and of a cathetus , the ratio is:
The trigonometric inverse function is:
in which
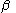is the angle opposite the cathetus 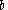.The adjacent angle of the catheti
, will be 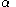= 90º –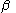 One may also obtain the value of the angle
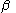by the equation:
in which
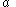is the other cathetus.See also
- CathetusCathetusIn a right triangle, the cathetus , commonly known as a leg, is either of the sides that are adjacent to the right angle. It is occasionally called the periphrasis . The side opposite the right angle is the hypotenuse...
- TriangleTriangleA triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
- Space diagonalSpace diagonalIn a rectangular box or a magic cube, the four space diagonals are the lines that go from a corner of the box or cube, through the center of the box or cube, to the opposite corner...
- Nonhypotenuse numberNonhypotenuse numberIn mathematics, a nonhypotenuse number is a natural number whose square cannot be written as the sum of two nonzero squares. The name stems from the fact that an edge of length equal to a nonhypotenuse number cannot form the hypotenuse of a right angle triangle with integer sides.The numbers 1, 2,...
- Taxicab geometryTaxicab geometryTaxicab geometry, considered by Hermann Minkowski in the 19th century, is a form of geometry in which the usual distance function or metric of Euclidean geometry is replaced by a new metric in which the distance between two points is the sum of the absolute differences of their coordinates...
- TrigonometryTrigonometryTrigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
- Special right trianglesSpecial right trianglesA special right triangle is a right triangle with some regular feature that makes calculations on the triangle easier, or for which simple formulas exist. For example, a right triangle may have angles that form simple relationships, such as 45-45-90. This is called an "angle-based" right triangle...