Special right triangles
Encyclopedia
A special right triangle is a right triangle
with some regular feature that makes calculations on the triangle easier, or for which simple formulas exist. For example, a right triangle may have angles that form simple relationships, such as 45-45-90. This is called an "angle-based" right triangle. A "side-based" right triangle is one in which the lengths of the sides form ratios of whole number
s, such as 3 : 4 : 5, or of other special numbers such as the golden ratio
. Knowing the relationships of the angles or ratios of sides of these special right triangles allows one to quickly calculate various lengths in geometric problems without resorting to more advanced methods.
The side lengths are generally deduced from the basis of the unit circle
or other geometric
methods. This approach may be used to rapidly reproduce the values of trigonometric functions for the angles 30°, 45°, and 60°.
Special triangles are used to aid in calculating common trigonometric functions, as below:
The 45-45-90 triangle, the 30-60-90 triangle, and the equilateral/equiangular (60-60-60) triangle are the three Möbius triangles in the plane, meaning that they tessellate the plane via reflections in their sides — see Triangle group
.
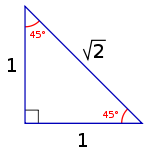In plane geometry, constructing the diagonal of a square results in a triangle whose three angles are in the ratio 1 : 1 : 2, adding up to 180° or π radians. Hence, the angles respectively measure 45° (π/4), 45° (π/4), and 90° (π/2). The sides in this triangle are in the ratio 1 : 1 : √2, which follows immediately from the Pythagorean theorem
.
Triangles with these angles are the only possible right triangles that are also isosceles triangles in Euclidean geometry. However, in spherical geometry
and hyperbolic geometry
, there are infinitely many different shapes of right isosceles triangles.
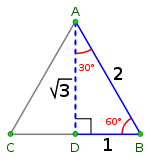This is a triangle whose three angles are in the ratio 1 : 2 : 3 and respectively measure 30°, 60°, and 90°. The sides are in the ratio 1 : √3 : 2.
The proof of this fact is clear using trigonometry
. The geometric
proof is simple:
The hemieq triangle is the only right triangle whose angles are in an arithmetic progression. The proof of this fact is simple and follows on from the fact that if α, α+δ, α+2δ are the angles in the progression then the sum of the angles 3α+3δ = 180°. So one angle must be 60° the other 90° leaving the remaining angle to be 30°.
. There is also a unique right triangle whose angles are in a geometric progression
. The three angles are π/(2φ2), π/(2φ), π/2 where the common ratio is φ, the golden ratio
. Consequently the angles are in the ratio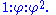
Based on the sine rule, the sides are in the ratio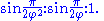
Because the sides are subject to the Pythagorean theorem
, this leads to the identity
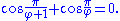
Interestingly, this can now be expanded into a phi identity that uses φ and the five fundamental mathematical constants π, e, i, 1, 0 of Euler's identity (though not as elegantly as the latter) as follows:
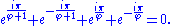
lengths, Pythagorean triple
s, possess angles that are never rational numbers of degrees
. They are most useful in that they may be easily remembered and any multiple
of the sides produces the same relationship. Using Euclid's formula for generating Pythagorean triples, the sides must be in the ratio
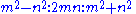
where m and n are any positive integers such that m>n.
The 3 : 4 : 5 triangles are the only right triangles with edges in arithmetic progression
. Triangles based on Pythagorean triples are Heronian
, meaning they have integer area as well as integer sides.
The following are all the Pythagorean triple ratios expressed in lowest form (beyond the five smallest ones, listed above) with both non-hypotenuse sides less than 256:
{0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...} is the length of the hypotenuse of a right triangle with integral sides, or in other words, the largest number in a Pythagorean triple. The length of the longer leg of this triangle is equal to the sum of the three sides of the preceding triangle in this series of triangles, and the shorter leg is equal to the difference between the preceding bypassed Fibonacci number and the shorter leg of the preceding triangle.
The first triangle in this series has sides of length 5, 4, and 3. Skipping 8, the next triangle has sides of length 13, 12 (5 + 4 + 3), and 5 (8 − 3). Skipping 21, the next triangle has sides of length 34, 30 (13 + 12 + 5), and 16 (21 − 5). This series continues indefinitely and approaches a limiting triangle with edge ratios:
This right triangle is sometimes referred to as a dom, a name suggested by Andrew Clarke to stress that this is the triangle obtained from dissecting a domino
along a diagonal. The dom forms the basis of the aperiodic
pinwheel tiling
proposed by John Conway
and Charles Radin.
differ by one. Such almost-isosceles right-angled triangles can be obtained recursively using Pell's equation
:
an is length of hypotenuse, n = 1, 2, 3, .... The smallest Pythagorean triples resulting are:
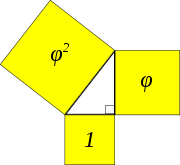
The Kepler triangle is a right triangle whose sides are in a geometric progression
. If the sides are formed from the geometric progression a, ar, ar2 then its common ratio r is given by r = √φ where φ is the golden ratio. Its sides are therefore in the ratio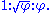
Right triangle
A right triangle or right-angled triangle is a triangle in which one angle is a right angle . The relation between the sides and angles of a right triangle is the basis for trigonometry.-Terminology:The side opposite the right angle is called the hypotenuse...
with some regular feature that makes calculations on the triangle easier, or for which simple formulas exist. For example, a right triangle may have angles that form simple relationships, such as 45-45-90. This is called an "angle-based" right triangle. A "side-based" right triangle is one in which the lengths of the sides form ratios of whole number
Whole number
Whole number is a term with inconsistent definitions by different authors. All distinguish whole numbers from fractions and numbers with fractional parts.Whole numbers may refer to:*natural numbers in sense — the positive integers...
s, such as 3 : 4 : 5, or of other special numbers such as the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
. Knowing the relationships of the angles or ratios of sides of these special right triangles allows one to quickly calculate various lengths in geometric problems without resorting to more advanced methods.
Angle-based
"Angle-based" special right triangles are specified by the relationships of the angles of which the triangle is composed. The angles of these triangles are such that the larger (right) angle, which is 90 degrees or π/2 radians, is equal to the sum of the other two angles.The side lengths are generally deduced from the basis of the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
or other geometric
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
methods. This approach may be used to rapidly reproduce the values of trigonometric functions for the angles 30°, 45°, and 60°.
Special triangles are used to aid in calculating common trigonometric functions, as below:
| Degrees | Radians | sin | cos | tan |
|---|---|---|---|---|
| 0 | 0 |  |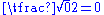
 |
 |
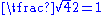| 30 |  |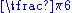
 |
 |
 |
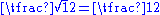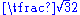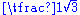| 45 |  |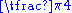
 |
 |
 |
| 60 |  |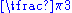
 |
 |
 |
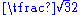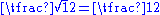| 90 |  |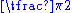
 |
 |
 |
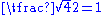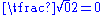The 45-45-90 triangle, the 30-60-90 triangle, and the equilateral/equiangular (60-60-60) triangle are the three Möbius triangles in the plane, meaning that they tessellate the plane via reflections in their sides — see Triangle group
Triangle group
In mathematics, a triangle group is a group that can be realized geometrically by sequences of reflections across the sides of a triangle. The triangle can be an ordinary Euclidean triangle, a triangle on the sphere, or a hyperbolic triangle...
.
45-45-90 triangle
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
.
Triangles with these angles are the only possible right triangles that are also isosceles triangles in Euclidean geometry. However, in spherical geometry
Spherical geometry
Spherical geometry is the geometry of the two-dimensional surface of a sphere. It is an example of a geometry which is not Euclidean. Two practical applications of the principles of spherical geometry are to navigation and astronomy....
and hyperbolic geometry
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
, there are infinitely many different shapes of right isosceles triangles.
30-60-90 triangle
The proof of this fact is clear using trigonometry
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
. The geometric
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
proof is simple:
- Draw an equilateral triangle ABC with side length 2 and with point D as the midpoint of segment BC. Draw an altitude line from A to D. Then ABD is a 30-60-90 (hemieq) triangle with hypotenuse of length 2, and base BD of length 1.
- The fact that the remaining leg AD has length √3 follows immediately from the Pythagorean theoremPythagorean theoremIn mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
.
The hemieq triangle is the only right triangle whose angles are in an arithmetic progression. The proof of this fact is simple and follows on from the fact that if α, α+δ, α+2δ are the angles in the progression then the sum of the angles 3α+3δ = 180°. So one angle must be 60° the other 90° leaving the remaining angle to be 30°.
Right triangle whose angles are in a geometric progression
The 30-60-90 triangle is the only right triangle whose angles are in an arithmetic progressionArithmetic progression
In mathematics, an arithmetic progression or arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant...
. There is also a unique right triangle whose angles are in a geometric progression
Geometric progression
In mathematics, a geometric progression, also known as a geometric sequence, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed non-zero number called the common ratio. For example, the sequence 2, 6, 18, 54, ... is a geometric progression...
. The three angles are π/(2φ2), π/(2φ), π/2 where the common ratio is φ, the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
. Consequently the angles are in the ratio
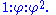
Based on the sine rule, the sides are in the ratio
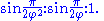Because the sides are subject to the Pythagorean theoremPythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
, this leads to the identity
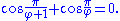
Interestingly, this can now be expanded into a phi identity that uses φ and the five fundamental mathematical constants π, e, i, 1, 0 of Euler's identity (though not as elegantly as the latter) as follows:
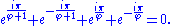
Side-based
Right triangles whose sides are of integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
lengths, Pythagorean triple
Pythagorean triple
A Pythagorean triple consists of three positive integers a, b, and c, such that . Such a triple is commonly written , and a well-known example is . If is a Pythagorean triple, then so is for any positive integer k. A primitive Pythagorean triple is one in which a, b and c are pairwise coprime...
s, possess angles that are never rational numbers of degrees
Degree (angle)
A degree , usually denoted by ° , is a measurement of plane angle, representing 1⁄360 of a full rotation; one degree is equivalent to π/180 radians...
. They are most useful in that they may be easily remembered and any multiple
Multiple
The word multiple can refer to:*Multiple , multiples of numbers*List of multiple discoveries, instances of scientists, working independently of each other, reaching similar findings...
of the sides produces the same relationship. Using Euclid's formula for generating Pythagorean triples, the sides must be in the ratio
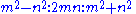
where m and n are any positive integers such that m>n.
Common Pythagorean triples
There are several Pythagorean triples which are very well known, including those with sides in the ratios:| 3: | 4 | :5 |
|---|---|---|
| 5: | 12 | :13 |
| 8: | 15 | :17 |
| 7: | 24 | :25 |
| 9: | 40 | :41 |
The 3 : 4 : 5 triangles are the only right triangles with edges in arithmetic progression
Arithmetic progression
In mathematics, an arithmetic progression or arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant...
. Triangles based on Pythagorean triples are Heronian
Heronian triangle
In geometry, a Heronian triangle is a triangle whose sidelengths and area are all rational numbers. It is named after Hero of Alexandria. Any such rational triangle can be scaled up to a corresponding triangle with integer sides and area, and often the term Heronian triangle is used to refer to...
, meaning they have integer area as well as integer sides.
The following are all the Pythagorean triple ratios expressed in lowest form (beyond the five smallest ones, listed above) with both non-hypotenuse sides less than 256:
| 11: | 60 | :61 |
|---|---|---|
| 12: | 35 | :37 |
| 13: | 84 | :85 |
| 15: | 112 | :113 |
| 16: | 63 | :65 |
| 17: | 144 | :145 |
| 19: | 180 | :181 |
| 20: | 21 | :29 |
| 20: | 99 | :101 |
| 21: | 220 | :221 |
| 24: | 143 | :145 |
|---|---|---|
| 28: | 45 | :53 |
| 28: | 195 | :197 |
| 32: | 255 | :257 |
| 33: | 56 | :65 |
| 36: | 77 | :85 |
| 39: | 80 | :89 |
| 44: | 117 | :125 |
| 48: | 55 | :73 |
| 51: | 140 | :149 |
| 52: | 165 | :173 |
|---|---|---|
| 57: | 176 | :185 |
| 60: | 91 | :109 |
| 60: | 221 | :229 |
| 65: | 72 | :97 |
| 84: | 187 | :205 |
| 85: | 132 | :157 |
| 88: | 105 | :137 |
| 95: | 168 | :193 |
| 96: | 247 | :265 |
| 104: | 153 | :185 |
|---|---|---|
| 105: | 208 | :233 |
| 115: | 252 | :277 |
| 119: | 120 | :169 |
| 120: | 209 | :241 |
| 133: | 156 | :205 |
| 140: | 171 | :221 |
| 160: | 231 | :281 |
| 161: | 240 | :289 |
| 204: | 253 | :325 |
Fibonacci triangles
Starting with 5, every other Fibonacci numberFibonacci number
In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
{0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...} is the length of the hypotenuse of a right triangle with integral sides, or in other words, the largest number in a Pythagorean triple. The length of the longer leg of this triangle is equal to the sum of the three sides of the preceding triangle in this series of triangles, and the shorter leg is equal to the difference between the preceding bypassed Fibonacci number and the shorter leg of the preceding triangle.
The first triangle in this series has sides of length 5, 4, and 3. Skipping 8, the next triangle has sides of length 13, 12 (5 + 4 + 3), and 5 (8 − 3). Skipping 21, the next triangle has sides of length 34, 30 (13 + 12 + 5), and 16 (21 − 5). This series continues indefinitely and approaches a limiting triangle with edge ratios:
This right triangle is sometimes referred to as a dom, a name suggested by Andrew Clarke to stress that this is the triangle obtained from dissecting a domino
Polyomino
A polyomino is a plane geometric figure formed by joining one or more equal squares edge to edge. It is a polyform whose cells are squares. It may be regarded as a finite subset of the regular square tiling with a connected interior....
along a diagonal. The dom forms the basis of the aperiodic
Aperiodic tiling
An aperiodic tiling is a tiling obtained from an aperiodic set of tiles. Properly speaking, aperiodicity is a property of particular sets of tiles; any given finite tiling is either periodic or non-periodic...
pinwheel tiling
Pinwheel tiling
Pinwheel tilings are non-periodic tilings defined by Charles Radin and based on a construction due to John Conway.They are the first known non-periodic tilings to each have the property that their tiles appear in infinitely many orientations....
proposed by John Conway
John Conway
John Conway may refer to:* John Horton Conway, mathematician at Princeton University. Popularly known for Conway's Game of Life* John B. Conway, mathematician, functional analyst, George Washington University...
and Charles Radin.
Almost-isosceles Pythagorean triples
Isosceles right-angled triangles cannot have sides with integer values. However, infinitely many almost-isosceles right triangles do exist. These are right-angled triangles with integral sides for which the lengths of the non-hypotenuse edgesCathetus
In a right triangle, the cathetus , commonly known as a leg, is either of the sides that are adjacent to the right angle. It is occasionally called the periphrasis . The side opposite the right angle is the hypotenuse...
differ by one. Such almost-isosceles right-angled triangles can be obtained recursively using Pell's equation
Pell's equation
Pell's equation is any Diophantine equation of the formx^2-ny^2=1\,where n is a nonsquare integer. The word Diophantine means that integer values of x and y are sought. Trivially, x = 1 and y = 0 always solve this equation...
:
- a0 = 1, b0 = 2
- an = 2bn–1 + an–1
- bn = 2an + bn–1
an is length of hypotenuse, n = 1, 2, 3, .... The smallest Pythagorean triples resulting are:
| 3: | 4 | :5 |
|---|---|---|
| 20: | 21 | :29 |
| 119: | 120 | :169 |
| 696: | 697 | :985 |
Right triangle whose sides are in a geometric progression
The Kepler triangle is a right triangle whose sides are in a geometric progression
Geometric progression
In mathematics, a geometric progression, also known as a geometric sequence, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed non-zero number called the common ratio. For example, the sequence 2, 6, 18, 54, ... is a geometric progression...
. If the sides are formed from the geometric progression a, ar, ar2 then its common ratio r is given by r = √φ where φ is the golden ratio. Its sides are therefore in the ratio
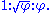
External links
- 3 : 4 : 5 triangle
- 30-60-90 triangle
- 45-45-90 triangle With interactive animations