
Aperiodic tiling
Encyclopedia
An aperiodic tiling is a tiling obtained from an aperiodic set of tiles. (The term is sometimes used loosely to refer to any non-periodic covering of the plane.) Properly speaking, aperiodicity is a property of particular sets of tiles; any given finite tiling is either periodic or non-periodic. Stated more formally, a tiling of the plane is aperiodic if and only if it consists of copies of a finite set of tiles, that themselves only admit non-periodic tilings.
A given set of tiles, in the Euclidean plane or some other geometric setting, admits a tiling if non-overlapping copies of the tiles in the set can be fitted together to cover the entire space. A given set of tiles might admit periodic tilings — that is, tilings which remain invariant after being shifted by a translation
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
(for example, a lattice of square tiles is periodic). It is not difficult to design a set of tiles that admits non-periodic tilings as well (for example, randomly arranged tilings using a 2×2 square and 2×1 rectangle will typically be non-periodic). An aperiodic set of tiles, however, admits only non-periodic tilings. Typically, distinct tilings may be obtained from a single aperiodic set of tiles.
The various Penrose tiles are the best-known examples of an aperiodic set of tiles.
Few methods for constructing aperiodic tilings are known. This is perhaps natural: the underlying undecidability
Undecidable problem
In computability theory and computational complexity theory, an undecidable problem is a decision problem for which it is impossible to construct a single algorithm that always leads to a correct yes-or-no answer....
of the Domino problem
Domino problem
In geometry, the domino problem is the problem of deciding whether a set of tiles of a particular kind admits a tiling.In a 1961 paper proposing a method for deciding an important case of David Hilbert's Entscheidungsproblem, the logician Hao Wang discussed tiling the plane by equally sized square...
implies that there exist aperiodic sets of tiles for which there can be no proof that they are aperiodic.
Quasicrystal
Quasicrystal
A quasiperiodic crystal, or, in short, quasicrystal, is a structure that is ordered but not periodic. A quasicrystalline pattern can continuously fill all available space, but it lacks translational symmetry...
s — physical materials with the apparent structure of the Penrose tilings — were discovered in 1984 by Dan Shechtman
Dan Shechtman
Dan Shechtman is the Philip Tobias Professor of Materials Science at the Technion – Israel Institute of Technology, an Associate of the US Department of Energy's Ames Laboratory, and Professor of Materials Science at Iowa State University. On April 8, 1982, while on sabbatical at the U.S...
et al.; however, the specific local structure of these materials is still poorly understood.
History
The second part of Hilbert's eighteenth problemHilbert's eighteenth problem
Hilbert's eighteenth problem is one of the 23 Hilbert problems set out in a celebrated list compiled in 1900 by mathematician David Hilbert. It asks three separate questions about lattices and sphere packing in Euclidean space....
asked for a single polyhedron tiling Euclidean 3-space, such that no tiling by it is isohedral (an anisohedral
Anisohedral tiling
In geometry, a shape is said to be anisohedral if it admits a tiling, but no such tiling is isohedral ; that is, in any tiling by that shape there are two tiles that are not equivalent under any symmetry of the tiling...
tile). The problem as stated was solved by Karl Reinhardt in 1928, but aperiodic tilings have been considered as a natural extension.
The specific question of aperiodic tiling first arose in 1961, when logician Hao Wang tried to determine whether the Domino Problem
Domino problem
In geometry, the domino problem is the problem of deciding whether a set of tiles of a particular kind admits a tiling.In a 1961 paper proposing a method for deciding an important case of David Hilbert's Entscheidungsproblem, the logician Hao Wang discussed tiling the plane by equally sized square...
is decidable — that is, whether there exists an algorithm for deciding if a given finite set of prototiles admits a tiling of the plane. Wang found algorithms to enumerate the tilesets that cannot tile the plane, and the tilesets that tile it periodically; by this he showed that such a decision algorithm exists if every finite set of prototiles that admits a tiling of the plane also admits a periodic tiling.
Robert Berger (mathematician)
Robert Berger is known for inventing the first aperiodic tiling using a set of 20,426 distinct tile shapes.The unexpected existence of aperiodic tilings, although not Berger's explicit construction of them, follows from another result proved by Berger: that the so-called domino problem is...
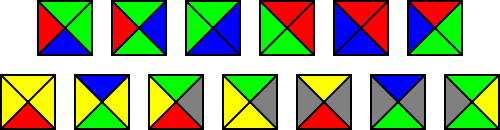
demonstrated that the tiling problem is in fact not decidable, it followed logically that there must exist an aperiodic set of prototiles. (Thus Wang's procedures do not work on all tile sets, although does not render them useless for practical purposes.) The first such set, presented by Berger and used in his proof of undecidability, required 20,426 Wang tiles. Berger later reduced his set to 104, and Hans Läuchli subsequently found an aperiodic set requiring only 40 Wang tiles. The set of 13 tiles given in the illustration on the right is an aperiodic set published by Karel Culik, II, in 1996.
However, a smaller aperiodic set, of six non-Wang tiles, was discovered by Raphael M. Robinson
Raphael M. Robinson
Raphael Mitchel Robinson was an American mathematician.Born in National City, California, Robinson was the youngest of four children of a lawyer and a teacher. He was awarded the BA , MA , and Ph.D. , all in mathematics, and all from the University of California, Berkeley. His Ph.D...
in 1971. Roger Penrose
Roger Penrose
Sir Roger Penrose OM FRS is an English mathematical physicist and Emeritus Rouse Ball Professor of Mathematics at the Mathematical Institute, University of Oxford and Emeritus Fellow of Wadham College...
discovered three more sets in 1973 and 1974, reducing the number of tiles needed to two, and Robert Ammann
Robert Ammann
Robert Ammann was an amateur mathematician who made several significant and groundbreaking contributions to the theory of quasicrystals and aperiodic tilings....
discovered several new sets in 1977.
In 1988, Peter Schmitt discovered a single aperiodic prototile in 3-dimensional Euclidean space. While no tiling by this prototile admits a translation as a symmetry, it has tilings with a screw symmetry
Screw axis
The screw axis of an object is a line that is simultaneously the axis of rotation and the line along which a translation occurs...
, the combination of a translation and a rotation through an irrational multiple of π. This was subsequently extended by John Horton Conway
John Horton Conway
John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
and Ludwig Danzer to a convex
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
aperiodic prototile, the Schmitt–Conway–Danzer tile. Because of the screw axis symmetry, this resulted in a reevaluation of the requirements for periodicity. Chaim Goodman-Strauss suggested that a protoset be considered strongly aperiodic if it admits no tiling with an infinite cyclic group of symmetries, and that other aperiodic protosets (such as the SCD tile) be called weakly aperiodic.
In 1996 Petra Gummelt showed that a single-marked decagonal tile, with two kinds of overlapping allowed, can force aperiodicity; this overlapping goes beyond the normal notion of tiling. An aperiodic protoset consisting of just one tile in the Euclidean plane, with no overlapping allowed, was proposed in early 2010 by Joshua Socolar; this example requires either matching conditions relating tiles that do not touch, or a disconnected but unmarked tile. The existence of a strongly aperiodic protoset consisting of just one tile in a higher dimension, or of a single simply connected tile in two dimensions without matching conditions, is an unsolved problem.
Constructions
There are remarkably few constructions of aperiodic sets of tiles known, even forty years after Berger's groundbreaking construction (Some constructions, such as that given in, are of infinite families of aperiodic sets of tiles). Moreover, those that have been found are generally constructed only a very few ways, primarily by forcing some sort of non-periodic hierarchical structure. Despite this, the undecidabilityUndecidable problem
In computability theory and computational complexity theory, an undecidable problem is a decision problem for which it is impossible to construct a single algorithm that always leads to a correct yes-or-no answer....
of the Domino Problem
Domino problem
In geometry, the domino problem is the problem of deciding whether a set of tiles of a particular kind admits a tiling.In a 1961 paper proposing a method for deciding an important case of David Hilbert's Entscheidungsproblem, the logician Hao Wang discussed tiling the plane by equally sized square...
ensures that there must be infinitely many distinct principles of construction, and that in fact, there exist aperiodic sets of tiles for which there can be no proof of their aperiodicity.
It is worth noting that there can be no aperiodic set of tiles in one dimension: it is a simple exercise to show that any set of tiles in the line either cannot be used to form a complete tiling, or can be used to form a periodic tiling. Aperiodicity requires two or more dimensions.
Aperiodic hierarchical tilings
To date, there is not a formal definition describing when a tiling has a hierarchical structure; nonetheless, it is clear that substitution tilings have them, as do the tilings of Berger, KnuthDonald Knuth
Donald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms...
, Läuchli and Robinson. As with the term "aperiodic tiling" itself, the term "aperiodic hierarchical tiling" is a convenient shorthand, meaning something along the lines of "a set of tiles admitting only non-periodic tilings with a hierarchical structure".
Each of these sets of tiles, in any tiling they admit, forces a particular hierarchical structure. (In many later examples, this structure can be described as a substitution tiling system; this is described below). No tiling admitted by such a set of tiles can be periodic, simply because no single translation can leave the entire hierarchical structure invariant. Consider Robinson's 1971 tiles:

This idea — of finding sets of tiles that can only admit hierarchical structures — has been used in the construction of most known aperiodic sets of tiles to date.
Substitutions
Substitution tiling systems provide a rich source of hierarchical non-periodic structures; however the substituted tiles themselves are not typically aperiodic. A set of tiles that forces a substitution structure to emerge is said to enforce the substitution structure. For example, the chair tiles shown below admit a substitution, and a portion of a substitution tiling is shown at right below. These substitution tilings are necessarily non-periodic, in precisely the same manner as described above, but the chair tile itself is not aperiodic—it is easy to find periodic tilings by unmarked chair tiles.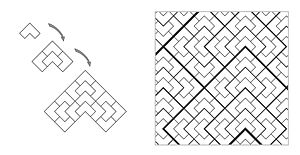
The Penrose tiles, and shortly thereafter Amman's several different sets of tiles, were the first example based on explicitly forcing a substitution tiling structure to emerge. Joshua Socolar, Roger Penrose
Roger Penrose
Sir Roger Penrose OM FRS is an English mathematical physicist and Emeritus Rouse Ball Professor of Mathematics at the Mathematical Institute, University of Oxford and Emeritus Fellow of Wadham College...
, Ludwig Danzer, and Chaim Goodman-Strauss have found several subsequent sets. Shahar Mozes gave the first general construction, showing that every product of one-dimensional substitution systems can be enforced by matching rules. Charles Radin found rules enforcing the Conway-pinwheel substitution tiling
Pinwheel tiling
Pinwheel tilings are non-periodic tilings defined by Charles Radin and based on a construction due to John Conway.They are the first known non-periodic tilings to each have the property that their tiles appear in infinitely many orientations....
system. In 1998, Goodman-Strauss showed that local matching rules can be found to force any substitution tiling structure, subject to some mild conditions.
Cut-and-project method
Non-periodic tilings can also be obtained by projection of higher-dimensional structures into spaces with lower dimensionality and under some circumstances there can be tiles that enforce this non-periodic structure and so are aperiodic. The Penrose tiles are the first and most famous example of this, as first noted in the pioneering work of de BruijnNicolaas Govert de Bruijn
Nicolaas Govert de Bruijn is a Dutch mathematician, affiliated as professor emeritus with the Eindhoven University of Technology. He received his Ph.D. in 1943 from Vrije Universiteit Amsterdam....
. There is yet no complete (algebraic) characterization of cut and project tilings that can be enforced by matching rules, although numerous necessary or sufficient conditions are known.
Other techniques
Only a few different kinds of constructions have been found. Notably, Jarkko KariJarkko Kari
Jarkko J. Kari is a Finnish mathematician and computer scientist, known for his contributions to the theory of Wang tiles and cellular automata. Kari is currently a professor at the Department of Mathematics, University of Turku.-Biography:...
gave an aperiodic set of Wang tiles based on multiplications by 2 or 2/3 of real numbers encoded by lines of tiles (the encoding is related to Sturmian sequences
Sturmian word
In mathematics, a Sturmian word, named after Jacques Charles François Sturm, is a certain kind of infinite word.- Definition :A word is a infinite sequence of symbols drawn from a finite alphabet. Call any finite contiguous subsequence of a word a factor...
made as the differences of consecutive elements of Beatty sequence
Beatty sequence
In mathematics, a Beatty sequence is the sequence of integers found by taking the floor of the positive multiplesof a positive irrational number...
s), with the aperiodicity mainly relying on the fact that 2^n/3^m is never equal to 1 for any positive integers n and m. This method was later adapted by Goodman-Strauss to give a strongly aperiodic set of tiles in the hyperbolic plane. Shahar Mozes has found many alternative constructions of aperiodic sets of tiles, some in more exotic settings; for example in semi-simple Lie Group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s. Joshua Socolar also gave another way to enforce aperiodicity, in terms of alternating condition. This generally leads to much smaller tile sets that the one derived from substitutions.
Physics of aperiodic tilings
Aperiodic tilings were considered as mathematical artefacts until 1984, when physicist Dan ShechtmanDan Shechtman
Dan Shechtman is the Philip Tobias Professor of Materials Science at the Technion – Israel Institute of Technology, an Associate of the US Department of Energy's Ames Laboratory, and Professor of Materials Science at Iowa State University. On April 8, 1982, while on sabbatical at the U.S...
announced the discovery of a phase of an aluminium-manganese alloy which produced a sharp diffractogram with an unambiguous fivefold symmetry – so it had to be a crystalline substance with icosahedral symmetry. In 1975 Robert Ammann
Robert Ammann
Robert Ammann was an amateur mathematician who made several significant and groundbreaking contributions to the theory of quasicrystals and aperiodic tilings....
had already extended the Penrose construction to a three dimensional icosahedral equivalent. In such cases the term 'tiling' is taken to mean 'filling the space'. Photonic devices are currently built as aperiodical sequences of different layers, being thus aperiodic in one direction and periodic in the other two. Quasicrystal structures of Cd-Te appear to consist of atomic layers in which the atoms are arranged in a planar aperiodic pattern. Sometimes an energetical minimum or a maximum of entropy occur for such aperiodic structures. Steinhardt has shown that Gummelt's overlapping decagons allow the application of an extremal principle and thus provide the link between the mathematics of aperiodic tiling and the structure of quasicrystals. Faraday wave
Faraday wave
Faraday waves, also known as Faraday ripples, named after Michael Faraday, are nonlinear standing waves that appear on liquids enclosed by a vibrating receptacle. When the vibration frequency exceeds a critical value, the flat hydrostatic surface becomes unstable. This is known as the Faraday...
s have been observed to form large patches of aperiodic patterns. The physics of this discovery has revived the interest in incommensurate structures and frequencies suggesting to link aperiodic tilings with interference phenomena.
Confusion regarding terminology
The terms non-periodic, quasiperiodic and aperiodic have been used in a wide variety of ways in a wide variety of fields, leading to considerable confusion. Moreover, the word "tiling" itself is quite problematic.In the context of 'Aperiodic tiling', a non-periodic tiling is simply one with no period, as discussed above, and aperiodicity is a property of tiles: a set of tiles is aperiodic if and only if it admits only non-periodic tilings. There is no mathematical concept of aperiodic tiling per se. Quasiperiodic tilings, generally, mean those obtained by the cut-and-project method; however William Thurston
William Thurston
William Paul Thurston is an American mathematician. He is a pioneer in the field of low-dimensional topology. In 1982, he was awarded the Fields Medal for his contributions to the study of 3-manifolds...
's influential lecture notes used the term to mean repetitive tilings. The Penrose tiles themselves are a source of much of the confusion, for the tilings they admit are quasiperiodic, in both senses, and non-periodic, and they themselves are aperiodic.
Moreover the terms aperiodic, non-periodic and quasiperiodic are widely used in other fields, such as dynamical systems, with altogether different meanings; and there is much literature on tilings in which, inappropriately, the distinction is not made. It is important to note however, that the core results of the field simply are not meaningful without this careful delineation.
The word "tiling" is problematic as well, despite its straightforward definition. There is no single Penrose tiling, for example: the Penrose rhombs admit infinitely many tilings (which cannot be distinguished locally) and even established figures in the field informally refer to "aperiodic tiling", knowing full well that this is not technically defined. A common solution is to try to use the terms carefully in technical writing, but recognize the widespread use of the informal terms.
See also
- Archimedean solidArchimedean solidIn geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices...
- Girih tilesGirih tilesGirih tiles are a set of five tiles that were used in the creation of tiling patterns for decoration of buildings in Islamic architecture...
- List of aperiodic sets of tiles
- QuasicrystalQuasicrystalA quasiperiodic crystal, or, in short, quasicrystal, is a structure that is ordered but not periodic. A quasicrystalline pattern can continuously fill all available space, but it lacks translational symmetry...
- ZelligeZelligeZellige, zillij or zellij is terra cotta tilework covered with enamel in the form of chips set into plaster. It is one of the main characteristics of the Moroccan architecture...

