Screw axis
Encyclopedia
The screw axis of an object
is a line that is simultaneously the axis of rotation
and the line along which a translation
occurs. Chasles' theorem shows that each Euclidean displacement
in three dimensional space has a screw axis, and the displacement can be decomposed into a rotation about and a slide along this screw axis.
Plücker coordinates
are used to locate a screw axis in space, and consist of a pair of three dimensional vectors. The first vector identifies the direction of the axis, and the second locates its position. The special case when the first vector is zero is interpreted as a pure translation in the direction of the second vector. A screw axis is associated each pair of vectors in the algebra of screws, also known as screw theory
.
The spatial movement of a body can be represented by a continuous set of displacements. Because each of these displacements has a screw axis, the movement has an associated ruled surface known as a screw surface. This surface is not the same as the axode, which is traced by the instantaneous screw axes of the movement of a body. The instantaneous screw axis, or 'instantaneous helical axis' (IHA), is the axis of the helicoidal field generated by the velocities of every point in a moving body.
When a spatial displacement specializes to a planar displacement, the screw axis becomes the displacement pole, and the instantaneous screw axis becomes the velocity pole, or instantaneous center of rotation, also called an instant center. The term centro is also used for a velocity pole, and the locus of these points for a planar movement is called a centrode
.
in 1830. Recently the work of Gulio Mozzi has been identified as presenting a similar result in 1763.
. Except for φ = 180°, we have to distinguish a screw displacement from its mirror image
. Unlike for rotations, a righthand and lefthand screw operation generate different groups.
The combination of a rotation about an axis and a translation in a perpendicular direction is a rotation about a parallel axis. However, a screw operation with a nonzero translation vector along the axis cannot be reduced like that. Thus the effect of a rotation combined with any translation is a screw operation in the general sense, with as special cases a pure translation. a pure rotation, and the identity. Together these are all the direct isometries in 3D.
Screw axis symmetry is invariance under a screw displacement. If φ = 360°/n for some positive integer n, then screw axis symmetry implies translational symmetry
with a translation vector which is n times that of the screw displacement.
Applicable for space group
s is a rotation by 360°/n about an axis, combined with a translation along the axis by a multiple of the distance of the translational symmetry, divided by n. This multiple is indicated by a subscript. So, 63 is a rotation of 60° combined with a translation of 1/2 of the lattice vector, implying that there is also 3-fold rotational symmetry
about this axis. The possibilities are 21, 31, 41, 42, 61, 62, and 63, and the enantiomorphous 32, 43, 64, and 65.
A non-discrete screw axis isometry group
contains all combinations of a rotation about some axis and a proportional translation along the axis (in rifling
, the constant of proportionality is called the twist rate); in general this is combined with k-fold rotational isometries about the same axis (k ≥ 1); the set of images of a point under the isometries is a k-fold helix
; in addition there may be a 2-fold rotation about a perpendicularly intersecting axis, and hence a k-fold helix of such axes.
defined by the matrix [A] and spatial translation
by the vector d. Coordinates x in a moving frame have coordinates X in the fixed frame given by: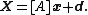
The screw axis of this displacement is the line S:P(t)=C+tS that remains in place before and after the spatial displacement. The vector S is the unit vector in the direction of the rotation axis of [A]. Points on this line translate by the amount k=(d·S) in the direction S.
A point on the screw axis satisfies the equation: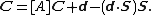
The term (d·S)S subtracts the slide along the screw axis in order to ensure that C exists.
Solve this equation for C using Cayley's formula for a rotation matrix [A]=[I-B]-1[I+B], where [B] is the skew-symmetric matrix constructed from Rodrigues' vector b=tan(φ/2)S such that [B]y=b×y. The result is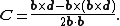
The screw axis of this spatial displacement is the line S defined by P(t)=C+tS. It has the Plücker coordinates
S=(S, C×S).
may be the combination of rotation about an axis (the screw axis) and a translation along that axis. This screw move is characterized by the velocity vector for the translation and the angular velocity
vector in the same or opposite direction. If these two vectors are constant and along one of the principal axes of the body, no external forces are needed for this motion (moving and spinning
). As an example, if gravity and drag are ignored, this is the motion of a bullet
fired from a rifled
gun
.
, when describing the motion of joints of the body. For any period of time, joint motion can be seen as the movement of a single point on one articulating surface with respect to the adjacent surface (usually distal with respect to proximal). The total translation and rotations along the path of motion can be defined as the time integrals of the instantaneous translation and rotation velocities at the IHA for a given reference time.
In any single plane
, the path formed by the locations of the moving instantaneous axis of rotation (IAR) is known as the 'centroid', and is used in the description of joint motion.
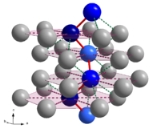
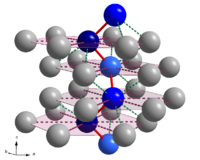In crystallography
, a screw axis is a symmetry operation describing how a combination of rotation about an axis and a translation parallel to that axis leaves a crystal unchanged.
Screw axes are noted by a number, n, where the angle of rotation is 360°/n. The degree of translation is then added as a subscript showing how far along the axis the translation is, as a portion of the parallel lattice vector. For example, 21 is a 180° (twofold) rotation followed by a translation of 1/2 of the lattice vector. 31 is a 120° (threefold) rotation followed by a translation of 1/3 of the lattice vector. The possible screw axes are 21, 31, 41, 42, 61, 62, and 63, and the enantiomorphous
32, 43, 64, and 65.
Entity
An entity is something that has a distinct, separate existence, although it need not be a material existence. In particular, abstractions and legal fictions are usually regarded as entities. In general, there is also no presumption that an entity is animate.An entity could be viewed as a set...
is a line that is simultaneously the axis of rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
and the line along which a translation
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
occurs. Chasles' theorem shows that each Euclidean displacement
Euclidean group
In mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...
in three dimensional space has a screw axis, and the displacement can be decomposed into a rotation about and a slide along this screw axis.
Plücker coordinates
Plücker coordinates
In geometry, Plücker coordinates, introduced by Julius Plücker in the 19th century, are a way to assign six homogenous coordinates to each line in projective 3-space, P3. Because they satisfy a quadratic constraint, they establish a one-to-one correspondence between the 4-dimensional space of lines...
are used to locate a screw axis in space, and consist of a pair of three dimensional vectors. The first vector identifies the direction of the axis, and the second locates its position. The special case when the first vector is zero is interpreted as a pure translation in the direction of the second vector. A screw axis is associated each pair of vectors in the algebra of screws, also known as screw theory
Screw theory
Screw theory refers to the algebra and calculus of pairs of vectors, such as forces and moments and angular and linear velocity, that arise in the kinematics and dynamics of rigid bodies....
.
The spatial movement of a body can be represented by a continuous set of displacements. Because each of these displacements has a screw axis, the movement has an associated ruled surface known as a screw surface. This surface is not the same as the axode, which is traced by the instantaneous screw axes of the movement of a body. The instantaneous screw axis, or 'instantaneous helical axis' (IHA), is the axis of the helicoidal field generated by the velocities of every point in a moving body.
When a spatial displacement specializes to a planar displacement, the screw axis becomes the displacement pole, and the instantaneous screw axis becomes the velocity pole, or instantaneous center of rotation, also called an instant center. The term centro is also used for a velocity pole, and the locus of these points for a planar movement is called a centrode
Centrode
Centrode in kinematics is the path traced by the instantaneous center of rotation of a rigid plane figure moving in a plane.-References:Homer D. Eckhardt Kinematic Design of Machines and Mechanisms, McGraw-Hill p. 63 ISBN 0070189536....
.
History
The proof that a spatial displacement can be decomposed into a rotation and slide around and along a line in space is attributed to Michel ChaslesMichel Chasles
Michel Floréal Chasles was a French mathematician.He was born at Épernon in France and studied at the École Polytechnique in Paris under Siméon Denis Poisson. In the War of the Sixth Coalition he was drafted to fight in the defence of Paris in 1814...
in 1830. Recently the work of Gulio Mozzi has been identified as presenting a similar result in 1763.
Screw axis of a spatial displacement
A screw displacement (also screw operation) is the composition of a rotation by an angle φ about an axis (called the screw axis) with a translation by a distance d along this axis. A positive rotation direction usually means one that corresponds to the translation direction by the right-hand ruleRight-hand rule
In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
. Except for φ = 180°, we have to distinguish a screw displacement from its mirror image
Mirror image
A mirror image is a reflected duplication of an object that appears identical but reversed. As an optical effect it results from reflection off of substances such as a mirror or water. It is also a concept in geometry and can be used as a conceptualization process for 3-D structures...
. Unlike for rotations, a righthand and lefthand screw operation generate different groups.
The combination of a rotation about an axis and a translation in a perpendicular direction is a rotation about a parallel axis. However, a screw operation with a nonzero translation vector along the axis cannot be reduced like that. Thus the effect of a rotation combined with any translation is a screw operation in the general sense, with as special cases a pure translation. a pure rotation, and the identity. Together these are all the direct isometries in 3D.
Screw axis symmetry is invariance under a screw displacement. If φ = 360°/n for some positive integer n, then screw axis symmetry implies translational symmetry
Translational symmetry
In geometry, a translation "slides" an object by a a: Ta = p + a.In physics and mathematics, continuous translational symmetry is the invariance of a system of equations under any translation...
with a translation vector which is n times that of the screw displacement.
Applicable for space group
Space group
In mathematics and geometry, a space group is a symmetry group, usually for three dimensions, that divides space into discrete repeatable domains.In three dimensions, there are 219 unique types, or counted as 230 if chiral copies are considered distinct...
s is a rotation by 360°/n about an axis, combined with a translation along the axis by a multiple of the distance of the translational symmetry, divided by n. This multiple is indicated by a subscript. So, 63 is a rotation of 60° combined with a translation of 1/2 of the lattice vector, implying that there is also 3-fold rotational symmetry
Rotational symmetry
Generally speaking, an object with rotational symmetry is an object that looks the same after a certain amount of rotation. An object may have more than one rotational symmetry; for instance, if reflections or turning it over are not counted, the triskelion appearing on the Isle of Man's flag has...
about this axis. The possibilities are 21, 31, 41, 42, 61, 62, and 63, and the enantiomorphous 32, 43, 64, and 65.
A non-discrete screw axis isometry group
Isometry group
In mathematics, the isometry group of a metric space is the set of all isometries from the metric space onto itself, with the function composition as group operation...
contains all combinations of a rotation about some axis and a proportional translation along the axis (in rifling
Rifling
Rifling is the process of making helical grooves in the barrel of a gun or firearm, which imparts a spin to a projectile around its long axis...
, the constant of proportionality is called the twist rate); in general this is combined with k-fold rotational isometries about the same axis (k ≥ 1); the set of images of a point under the isometries is a k-fold helix
Helix
A helix is a type of smooth space curve, i.e. a curve in three-dimensional space. It has the property that the tangent line at any point makes a constant angle with a fixed line called the axis. Examples of helixes are coil springs and the handrails of spiral staircases. A "filled-in" helix – for...
; in addition there may be a 2-fold rotation about a perpendicularly intersecting axis, and hence a k-fold helix of such axes.
Formula for the screw axis
A spatial displacement, T=([A],d), is the Euclidean transformation consisting of the spatial rotationRotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
defined by the matrix [A] and spatial translation
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
by the vector d. Coordinates x in a moving frame have coordinates X in the fixed frame given by:
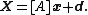
The screw axis of this displacement is the line S:P(t)=C+tS that remains in place before and after the spatial displacement. The vector S is the unit vector in the direction of the rotation axis of [A]. Points on this line translate by the amount k=(d·S) in the direction S.
A point on the screw axis satisfies the equation:
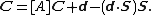
The term (d·S)S subtracts the slide along the screw axis in order to ensure that C exists.
Solve this equation for C using Cayley's formula for a rotation matrix [A]=[I-B]-1[I+B], where [B] is the skew-symmetric matrix constructed from Rodrigues' vector b=tan(φ/2)S such that [B]y=b×y. The result is
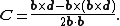
The screw axis of this spatial displacement is the line S defined by P(t)=C+tS. It has the Plücker coordinates
Plücker coordinates
In geometry, Plücker coordinates, introduced by Julius Plücker in the 19th century, are a way to assign six homogenous coordinates to each line in projective 3-space, P3. Because they satisfy a quadratic constraint, they establish a one-to-one correspondence between the 4-dimensional space of lines...
S=(S, C×S).
Mechanics
The motion of a rigid bodyRigid body
In physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it...
may be the combination of rotation about an axis (the screw axis) and a translation along that axis. This screw move is characterized by the velocity vector for the translation and the angular velocity
Angular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
vector in the same or opposite direction. If these two vectors are constant and along one of the principal axes of the body, no external forces are needed for this motion (moving and spinning
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
). As an example, if gravity and drag are ignored, this is the motion of a bullet
Bullet
A bullet is a projectile propelled by a firearm, sling, or air gun. Bullets do not normally contain explosives, but damage the intended target by impact and penetration...
fired from a rifled
Rifling
Rifling is the process of making helical grooves in the barrel of a gun or firearm, which imparts a spin to a projectile around its long axis...
gun
Gun
A gun is a muzzle or breech-loaded projectile-firing weapon. There are various definitions depending on the nation and branch of service. A "gun" may be distinguished from other firearms in being a crew-served weapon such as a howitzer or mortar, as opposed to a small arm like a rifle or pistol,...
.
Biomechanics
This parameter is often used in biomechanicsBiomechanics
Biomechanics is the application of mechanical principles to biological systems, such as humans, animals, plants, organs, and cells. Perhaps one of the best definitions was provided by Herbert Hatze in 1974: "Biomechanics is the study of the structure and function of biological systems by means of...
, when describing the motion of joints of the body. For any period of time, joint motion can be seen as the movement of a single point on one articulating surface with respect to the adjacent surface (usually distal with respect to proximal). The total translation and rotations along the path of motion can be defined as the time integrals of the instantaneous translation and rotation velocities at the IHA for a given reference time.
In any single plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
, the path formed by the locations of the moving instantaneous axis of rotation (IAR) is known as the 'centroid', and is used in the description of joint motion.
Crystallography
Crystallography
Crystallography is the experimental science of the arrangement of atoms in solids. The word "crystallography" derives from the Greek words crystallon = cold drop / frozen drop, with its meaning extending to all solids with some degree of transparency, and grapho = write.Before the development of...
, a screw axis is a symmetry operation describing how a combination of rotation about an axis and a translation parallel to that axis leaves a crystal unchanged.
Screw axes are noted by a number, n, where the angle of rotation is 360°/n. The degree of translation is then added as a subscript showing how far along the axis the translation is, as a portion of the parallel lattice vector. For example, 21 is a 180° (twofold) rotation followed by a translation of 1/2 of the lattice vector. 31 is a 120° (threefold) rotation followed by a translation of 1/3 of the lattice vector. The possible screw axes are 21, 31, 41, 42, 61, 62, and 63, and the enantiomorphous
Chirality (mathematics)
In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.A chiral object...
32, 43, 64, and 65.
See also
- Helical symmetry
- Euler's rotation theoremEuler's rotation theoremIn geometry, Euler's rotation theorem states that, in three-dimensional space, any displacement of a rigid body such that a point on the rigid body remains fixed, is equivalent to a single rotation about some axis that runs through the fixed point. It also means that the composition of two...
– rotations without translation - Screw theoryScrew theoryScrew theory refers to the algebra and calculus of pairs of vectors, such as forces and moments and angular and linear velocity, that arise in the kinematics and dynamics of rigid bodies....
- Space groupSpace groupIn mathematics and geometry, a space group is a symmetry group, usually for three dimensions, that divides space into discrete repeatable domains.In three dimensions, there are 219 unique types, or counted as 230 if chiral copies are considered distinct...
- Corkscrew (roller coaster element)