In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, the domino problem is the problem of deciding

Decision problem

In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...

 whether a set of tiles of a particular kind admits a tiling

Tessellation

A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...

.

In a 1961 paper proposing a method for deciding an important case of David Hilbert

David Hilbert

David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...

's Entscheidungsproblem

Entscheidungsproblem

In mathematics, the is a challenge posed by David Hilbert in 1928. The asks for an algorithm that will take as input a description of a formal language and a mathematical statement in the language and produce as output either "True" or "False" according to whether the statement is true or false...

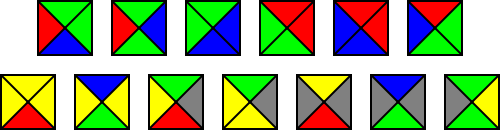
, the logician Hao Wang discussed tiling the plane by equally sized square plates with colored edges, now called Wang tiles or Wang dominoes. A domino set is a finite set of such plates that may not be rotated or reflected, each colored in a different way. A domino set is solvable if an infinite plane, ruled by squares of the same size as the dominoes, can be covered by copies of dominoes in the set, with a domino on each square, in such a way that colors on adjacent domino edges match.

According to Wang's student, Robert Berger

Robert Berger (mathematician)

Robert Berger is known for inventing the first aperiodic tiling using a set of 20,426 distinct tile shapes.The unexpected existence of aperiodic tilings, although not Berger's explicit construction of them, follows from another result proved by Berger: that the so-called domino problem is...

,

The Domino Problem deals with the class of all domino sets. It consists of deciding, for each domino set, whether or not it is solvable. We say that the Domino Problem is or according to whether there exists or does not exist an algorithm which, given the specifications of an arbitrary domino set, will decide whether or not the set is solvable.

In other words, is there an effective procedure for settling the problem for any given domino set?

Wang made the following

Fundamental Conjecture:
A finite set of plates is solvable if and only if there exists a cyclic rectangle of the plates; or in other words, a finite set of plates is solvable if and only if it has at least one periodic solution.

In short, he conjectured that there is no aperiodic domino set

Aperiodic tiling

An aperiodic tiling is a tiling obtained from an aperiodic set of tiles. Properly speaking, aperiodicity is a property of particular sets of tiles; any given finite tiling is either periodic or non-periodic...

. Wang observed that if this conjecture is true, then the Domino Problem is decidable. If every domino set either does not admit a tiling, or admits a periodic tiling, then there is an algorithm for deciding which is the case: enumerate all possible coverings of larger and larger rectangles until either there is some size of rectangle that the tiles cannot cover, or until a fundamental domain

Fundamental domain

In geometry, the fundamental domain of a symmetry group of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry. More rigorously, given a topological space and a group acting on it, the images of a single point under the group...

 for a periodic tiling is found. Either way, the algorithm will eventually halt, so long as no aperiodic set exists.

This observation holds in a wide range of settings, such as tiling by unmarked polygons: if there is no aperiodic set, it suffices to enumerate all possible configurations of any given set of tiles and check whether the configuration is a fundamental domain for some periodic tiling.

In 1966, Berger proved the Domino Problem is undecidable for Wang dominoes (and implicitly, for planar tiles in general), incidentally giving an aperiodic set

Aperiodic tiling

An aperiodic tiling is a tiling obtained from an aperiodic set of tiles. Properly speaking, aperiodicity is a property of particular sets of tiles; any given finite tiling is either periodic or non-periodic...

 of over 20,000 Wang dominoes. (In his unpublished Ph.D. thesis, he gives a smaller set of 104.)

Raphael Robinson reworked Berger's proof in 1971 paper and provided a smaller domino set.