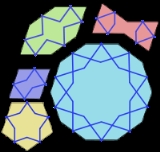
Girih tiles
Encyclopedia

Tile
A tile is a manufactured piece of hard-wearing material such as ceramic, stone, metal, or even glass. Tiles are generally used for covering roofs, floors, walls, showers, or other objects such as tabletops...
s that were used in the creation of tiling patterns for decoration of buildings in Islamic architecture
Islamic architecture
Islamic architecture encompasses a wide range of both secular and religious styles from the foundation of Islam to the present day, influencing the design and construction of buildings and structures in Islamic culture....
. They are known to have been used since about the year 1200 and their arrangements found significant improvement starting with the Darb-i Imam
Darb-i Imam
The shrine of Darb-e Imam, located in the Dardasht quarter of Isfahan, Iran, is a funerary complex, with a cemetery, shrine structures, and courtyards belonging to different construction periods and styles...
shrine in Isfahan in Iran
Iran
Iran , officially the Islamic Republic of Iran , is a country in Southern and Western Asia. The name "Iran" has been in use natively since the Sassanian era and came into use internationally in 1935, before which the country was known to the Western world as Persia...
built in 1453.
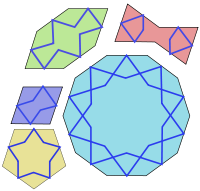
The five shapes of the tiles are:
- a regular decagonDecagonIn geometry, a decagon is any polygon with ten sides and ten angles, and usually refers to a regular decagon, having all sides of equal length and each internal angle equal to 144°...
with ten interior angles of 144°; - an elongated (irregular convex) hexagon with interior angles of 72°, 144°, 144°, 72°, 144°, 144°;
- a bow tieBow tieThe bow tie is a type of men's necktie. It consists of a ribbon of fabric tied around the collar in a symmetrical manner such that the two opposite ends form loops. Ready-tied bow ties are available, in which the distinctive bow is sewn into shape and the band around the neck incorporates a clip....
(non-convex hexagon) with interior angles of 72°, 72°, 216°, 72°, 72°, 216°; - a rhombusRhombusIn Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every...
with interior angles of 72°, 108°, 72°, 108°; and - a regular pentagonPentagonIn geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...
with five interior angles of 108°.
All sides of these figures have the same length; and all their angles are multiples of 36° (π/5). All of them, except the pentagon, have bilateral (reflection) symmetry through two perpendicular lines. Some have additional symmetries. Specifically, the decagon has tenfold rotational symmetry (rotation by 36°); and the pentagon has fivefold rotational symmetry (rotation by 72°).
Girih are lines (strapwork
Strapwork
In the history of art and design, the term strapwork refers to a stylised representation in ornament of strips or bands of curling leather, parchment or metal cut into elaborate shapes, with piercings and often interwoven...
) which decorate the tiles. The tiles are used to form girih patterns, from the Persian word for "knot". In most cases, only the girih (and other minor decorations like flowers) are visible rather than the boundaries of the tiles themselves. The girih are piece-wise straight lines which cross the boundaries of the tiles at the center of an edge at 54° (3π/10) to the edge. Two intersecting girih cross each edge of a tile. Most tiles have a unique pattern of girih inside the tile which are continuous and follow the symmetry of the tile. However, the decagon has two possible girih patterns one of which has only fivefold rather than tenfold rotational symmetry.
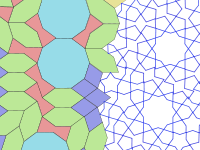
Periodic or aperiodic?
Most uses of girih tiling in Islamic architecture were periodic; they had unit cells that were repeated in the same orientation within a lattice. Some had patterns which could not be extended to a tiling of the entire plane. None of them are known to have had patterns that could be extended to the entire plane only in an aperiodic way.However, on some buildings, the large girih tiles were decorated with patterns that formed small girih tiles. And on one of these, Darb-i Imam
Darb-i Imam
The shrine of Darb-e Imam, located in the Dardasht quarter of Isfahan, Iran, is a funerary complex, with a cemetery, shrine structures, and courtyards belonging to different construction periods and styles...
, the subdivision into smaller tiles was done in a way that could have been generalized to an aperiodic tiling
Aperiodic tiling
An aperiodic tiling is a tiling obtained from an aperiodic set of tiles. Properly speaking, aperiodicity is a property of particular sets of tiles; any given finite tiling is either periodic or non-periodic...
of the plane.
Mathematics of girih tilings

Peter Lu
Peter James Lu, PhD is a post-doctoral research fellow in the Department of Physics and the School of Engineering and Applied Sciences at Harvard University in Cambridge, Massachusetts...
of Harvard University
Harvard University
Harvard University is a private Ivy League university located in Cambridge, Massachusetts, United States, established in 1636 by the Massachusetts legislature. Harvard is the oldest institution of higher learning in the United States and the first corporation chartered in the country...
and Professor Paul J. Steinhardt
Paul Steinhardt
Paul J. Steinhardt is the Albert Einstein Professor of Science at Princeton University and a professor of theoretical physics. He received his B.S. at the California Institute of Technology and his Ph.D. in Physics at Harvard University...
of Princeton University
Princeton University
Princeton University is a private research university located in Princeton, New Jersey, United States. The school is one of the eight universities of the Ivy League, and is one of the nine Colonial Colleges founded before the American Revolution....
published a paper in the journal Science suggesting that girih tilings possessed properties consistent with self-similar fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
quasicrystalline tilings such as Penrose tiling
Penrose tiling
A Penrose tiling is a non-periodic tiling generated by an aperiodic set of prototiles named after Sir Roger Penrose, who investigated these sets in the 1970s. The aperiodicity of the Penrose prototiles implies that a shifted copy of a Penrose tiling will never match the original...
s (presentation 1974, predecessor works starting in about 1964) predating them by five centuries.
This finding was supported both by analysis of patterns on surviving structures, and by examination of 15th century Persian scrolls. However, we have no indication of how much more the architects may have known about the mathematics involved. It is generally believed that such designs were constructed by drafting zigzag outlines with only a straightedge and a compass. Templates found on scrolls such as the 97 foot (29.5 metres) long Topkapi Scroll
Topkapı Scroll
The Topkapi Scroll is a Timurid dynasty pattern scroll in the collection of the Topkapi Palace museum.The scroll is a valuable source of information, consisting of 114 patterns that may have been used both indirectly and directly by architects to create the tiling patterns in many mosques around...
may have been consulted. Found in the Topkapi Palace
Topkapi Palace
The Topkapı Palace is a large palace in Istanbul, Turkey, that was the primary residence of the Ottoman Sultans for approximately 400 years of their 624-year reign....
in Istanbul, the administrative center of the Ottoman Empire and believed to date from the late 15th century, the scroll shows a succession of two- and three- dimensional geometric patterns. There is no text, but there is a grid pattern and color-coding used to highlight symmetries and distinguish three-dimensional projections. Drawings such as shown on this scroll would have served as pattern-books for the artisans who fabricated the tiles, and the shapes of the girih tiles then would dictate how they could be combined into large patterns. In this way, craftsmen could make highly complex designs without resorting to mathematics and without necessarily understanding their underlying principles.
This use of repeating patterns created from a limited number of geometric shapes available to craftsmen of the day is similar to the practice of contemporary European Gothic artisans. Designers of both styles were concerned with using their inventories of geometrical shapes to create the maximum diversity of forms. This is using a skill and practice very different from mathematics.

