Polyomino - AbsoluteAstronomy.com

A polyomino is a plane geometric figure formed by joining one or more equal squares edge to edge. It is a polyform

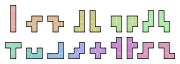
Polyform

In recreational mathematics, a polyform is a plane figure constructed by joining together identical basic polygons. The basic polygon is often a convex plane-filling polygon, such as a square or a triangle. More specific names have been given to polyforms resulting from specific basic polygons, as...

whose cells are squares

Square (geometry)

In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...

. It may be regarded as a finite subset of the regular square tiling with a connected

Connected space

In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...

interior

Interior (topology)

In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....

.

Polyominoes are classified according to how many cells they have:

Number of cells	Name
1	monomino
2	domino Domino (mathematics) In mathematics, a domino is a polyomino of order 2, that is, a polygon in the plane made of two equal-sized squares connected edge-to-edge. When rotations and reflections are not considered to be distinct shapes, there is only one free domino....
3	tromino Tromino A tromino is a polyomino of order 3, that is, a polygon in the plane made of three equal-sized squares connected edge-to-edge... or triomino
4	tetromino Tetromino A tetromino is a geometric shape composed of four squares, connected orthogonally. This, like dominoes and pentominoes, is a particular type of polyomino...
5	pentomino Pentomino A pentomino is a polyomino composed of five congruent squares, connected along their edges .... or pentamino
6	hexomino Hexomino A hexomino is a polyomino of order 6, that is, a polygon in the plane made of 6 equal-sized squares connected edge-to-edge. The name of this type of figure is formed with the prefix hex-. When rotations and reflections are not considered to be distinct shapes, there are 35 different free hexominoes...
7	heptomino Heptomino A heptomino is a polyomino of order 7, that is, a polygon in the plane made of 7 equal-sized squares connected edge-to-edge. The name of this type of figure is formed with the prefix hept-. When rotations and reflections are not considered to be distinct shapes, there are 108 different free...
8	octomino Octomino An octomino is a polyomino of order 8, that is, a polygon in the plane made of 8 equal-sized squares connected edge-to-edge. The name of this type of figure is formed with the prefix oct-. When rotations and reflections are not considered to be distinct shapes, there are 369 different free...
9	nonomino Nonomino A nonomino is a polyomino of order 9, that is, a polygon in the plane made of 9 equal-sized squares connected edge-to-edge. The name of this type of figure is formed with the prefix non-. When rotations and reflections are not considered to be distinct shapes, there are 1,285 different free... or enneomino
10	decomino
11	undecomino or hendecomino
12	dodecomino

Polyominoes have been used in popular puzzle

Puzzle

A puzzle is a problem or enigma that tests the ingenuity of the solver. In a basic puzzle, one is intended to put together pieces in a logical way in order to come up with the desired solution...

s since at least 1907, and the enumeration of pentominoes is dated to antiquity. Many results with the pieces of 1 to 6 squares were first published in Fairy Chess Review

Fairy Chess Review

The Fairy Chess Review was a magazine that was devoted principally to fairy chess problems but also included extensive original results on related questions in mathematical recreations such as knight's tours and polyominos as well as much else, such as chess-related word puzzles...

between the years 1937 to 1957, under the name of “dissection problems.” The name polyomino was invented by Solomon W. Golomb

Solomon W. Golomb

Solomon Wolf Golomb is an American mathematician and engineer and a professor of electrical engineering at the University of Southern California, best known to the general public and fans of mathematical games as the inventor of polyominoes, the inspiration for the computer game Tetris...

in 1953 and it was popularized by Martin Gardner

Martin Gardner

Martin Gardner was an American mathematics and science writer specializing in recreational mathematics, but with interests encompassing micromagic, stage magic, literature , philosophy, scientific skepticism, and religion...

.

Related to polyominoes are polyiamond

Polyiamond

A polyiamond is a polyform whose base form is an equilateral triangle. The word polyiamond is a back-formation from diamond, because this word is often used to describe the shape of a pair of equilateral triangles placed base to base, and the initial "di-" looked like a Greek prefix meaning...

s, formed from equilateral triangles; polyhexes

Polyhex (mathematics)

In recreational mathematics, a polyhex is a polyform with a regular hexagon as the base form.As with polyominoes, polyhexes may be enumerated as free polyhexes , fixed polyhexes and one-sided polyhexes In recreational mathematics, a polyhex is a polyform with a regular hexagon (or 'hex' for...

, formed from regular hexagons; and other plane polyform

Polyform

s. Polyominoes have been generalised to higher dimension

Dimension

In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...

s by joining cubes to form polycube

Polycube

s, or hypercube

Hypercube

In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...

s to form polyhypercubes.

Like many puzzles in recreational mathematics, polyominoes raise many combinatorial

Combinatorics

Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...

problems. The most basic is enumerating

Enumeration

In mathematics and theoretical computer science, the broadest and most abstract definition of an enumeration of a set is an exact listing of all of its elements . The restrictions imposed on the type of list used depend on the branch of mathematics and the context in which one is working...

polyominoes of a given size. No formula has been found except for special classes of polyominoes. A number of estimates are known, and there are algorithm

Algorithm

In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...

s for calculating them.

Polyominoes with holes are inconvenient for some purposes, such as tiling problems. In some contexts polyominoes with holes are excluded, allowing only simply connected polyominoes.

Free, one-sided, and fixed polyominoes

There are three common ways of distinguishing polyominoes for enumeration:

free polyominoes are distinct when none is a rigid transformation (translation
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...

, rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...

, reflection
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...

or glide reflection
Glide reflection
In geometry, a glide reflection is a type of isometry of the Euclidean plane: the combination of a reflection in a line and a translation along that line. Reversing the order of combining gives the same result...

) of another (pieces that can be picked up and flipped over).
one-sided polyominoes are distinct when none is a translation or rotation of another (pieces that cannot be flipped over).
fixed polyominoes are distinct when none is a translation of another (pieces that can be neither flipped nor rotated).

The following table shows the numbers of polyominoes of various types with n cells.

n	name (OEIS sequence)
1	monomino	1	0	1	1	1
2	domino Domino (mathematics) In mathematics, a domino is a polyomino of order 2, that is, a polygon in the plane made of two equal-sized squares connected edge-to-edge. When rotations and reflections are not considered to be distinct shapes, there is only one free domino....	1	0	1	1	2
3	tromino Tromino A tromino is a polyomino of order 3, that is, a polygon in the plane made of three equal-sized squares connected edge-to-edge... or triomino	2	0	2	2	6
4	tetromino Tetromino A tetromino is a geometric shape composed of four squares, connected orthogonally. This, like dominoes and pentominoes, is a particular type of polyomino...	5	0	5	7	19
5	pentomino Pentomino A pentomino is a polyomino composed of five congruent squares, connected along their edges ....	12	0	12	18	63
6	hexomino Hexomino A hexomino is a polyomino of order 6, that is, a polygon in the plane made of 6 equal-sized squares connected edge-to-edge. The name of this type of figure is formed with the prefix hex-. When rotations and reflections are not considered to be distinct shapes, there are 35 different free hexominoes...	35	0	35	60	216
7	heptomino Heptomino A heptomino is a polyomino of order 7, that is, a polygon in the plane made of 7 equal-sized squares connected edge-to-edge. The name of this type of figure is formed with the prefix hept-. When rotations and reflections are not considered to be distinct shapes, there are 108 different free...	108	1	107	196	760
8	octomino Octomino An octomino is a polyomino of order 8, that is, a polygon in the plane made of 8 equal-sized squares connected edge-to-edge. The name of this type of figure is formed with the prefix oct-. When rotations and reflections are not considered to be distinct shapes, there are 369 different free...	369	6	363	704	2,725
9	nonomino Nonomino A nonomino is a polyomino of order 9, that is, a polygon in the plane made of 9 equal-sized squares connected edge-to-edge. The name of this type of figure is formed with the prefix non-. When rotations and reflections are not considered to be distinct shapes, there are 1,285 different free... or enneomino	1,285	37	1,248	2,500	9,910
10	decomino	4,655	195	4,460	9,189	36,446
11	undecomino	17,073	979	16,094	33,896	135,268
12	dodecomino	63,600	4,663	58,937	126,759	505,861

, Iwan Jensen has enumerated the fixed polyominoes up to n=56; the number of fixed polyominoes with 56 cells is approximately 6.915×10³¹. Free polyominoes have been enumerated up to n=28 by Tomás Oliveira e Silva.

Symmetries of polyominoes

The dihedral group

Dihedral group

In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...

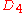is the group

Group (mathematics)

In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...

of symmetries

Symmetry

Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...

(symmetry group

Symmetry group

The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...

) of a square. This group contains four rotations and four reflections. It is generated by alternating reflections about the x-axis and about a diagonal. One free polyomino corresponds to at most 8 fixed polyominoes, which are its images under the symmetries of

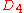. However, those images are not necessarily distinct: the more symmetry a free polyomino has, the fewer distinct fixed counterparts it has. Therefore, a free polyomino which is invariant under some or all non-trivial symmetries of

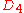may correspond to only 4, 2 or 1 fixed polyominoes. Mathematically, free polyominoes are equivalence classes of fixed polyominoes under the group

.

Polyominoes have the following possible symmetries; the least number of squares needed in a polyomino with that symmetry is given in each case:

8 fixed polyominoes for each free polyomino:
- no symmetry (4)
4 fixed polyominoes for each free polyomino:
- mirror symmetry with respect to one of the grid line directions (4)
- mirror symmetry with respect to a diagonal line (3)
- 2-fold rotational symmetry: 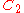(4)
2 fixed polyominoes for each free polyomino:
- symmetry with respect to both grid line directions, and hence also 2-fold rotational symmetry: 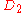(2)
- symmetry with respect to both diagonal directions, and hence also 2-fold rotational symmetry: 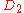(7)
- 4-fold rotational symmetry: (8)
1 fixed polyomino for each free polyomino:
- all symmetry of the square: (1).

The following table shows the numbers of polyominoes with n squares, sorted by symmetry groups.

n					(90°)	(45°)
1	0	0	0	0	0	0	0	1
2	0	0	0	0	1	0	0	0
3	0	0	1	0	1	0	0	0
4	1	1	0	1	1	0	0	1
5	5	2	2	1	1	0	0	1
6	20	6	2	5	2	0	0	0
7	84	9	7	4	3	1	0	0
8	316	23	5	18	4	1	1	1
9	1,196	38	26	19	4	0	0	2
10	4,461	90	22	73	8	1	0	0
11	16,750	147	91	73	10	2	0	0
12	62,878	341	79	278	15	3	3	3

Inductive algorithms

Each polyomino of order n+1 can be obtained by adding a square to a polyomino of order n. This leads to algorithms for generating polyominoes inductively.

Most simply, given a list of polyominoes of order n, squares may be added next to each polyomino in each possible position, and the resulting polyomino of order n+1 added to the list if not a duplicate of one already found; refinements in ordering the enumeration and marking adjacent squares that should not be considered reduce the number of cases that need to be checked for duplicates. This method may be used to enumerate either free or fixed polyominoes.

A more sophisticated method, described by Redelmeier, has been used by many authors as a way of not only counting polyominoes (without requiring that all polyominoes of order n be stored in order to enumerate those of order n+1), but also proving upper bounds on their number. The basic idea is that we begin with a single square, and from there, recursively add squares. Depending on the details, it may count each n-omino n times, once from starting from each of its n squares, or may be arranged to count each once only.

The simplest implementation involves adding one square at a time. Beginning with an initial square, number the adjacent squares, clockwise from the top, 1, 2, 3, and 4. Now pick a number between 1 and 4, and add a square at that location. Number the unnumbered adjacent squares, starting with 5. Then, pick a number larger than the previously picked number, and add that square. Continue picking a number larger than the number of the current square, adding that square, and then numbering the new adjacent squares. When n squares have been created, an n-omino has been created.

This method ensures that each fixed polyomino is counted exactly n times, once for each starting square. It can be optimized so that it counts each polyomino only once, rather than n times. Starting with the initial square, declare it to be the lower-left square of the polyomino. Simply do not number any square which is on a lower row, or left of the square on the same row. This is the version described by Redelmeier.

If one wishes to count free polyominoes instead, then one may check for symmetries after creating each n-omino. However, it is faster to generate symmetric polyominoes separately (by a variation of this method) and so determine the number of free polyominoes by Burnside's lemma

Burnside's lemma

Burnside's lemma, sometimes also called Burnside's counting theorem, the Cauchy-Frobenius lemma or the orbit-counting theorem, is a result in group theory which is often useful in taking account of symmetry when counting mathematical objects. Its various eponyms include William Burnside, George...

Transfer-matrix method

The most modern algorithm for enumerating the fixed polyominoes was discovered by Iwan Jensen. An improvement on Andrew Conway

Andrew Conway

Andrew Conway is a professional rugby union player for Blackrock College RFC and Leinster Rugby. Conway made his senior debut for Leinster in the Magners League against the Scarlets as a late substitution where he set up Jonathan Sexton's try. He made his starting debut for Leinster on the 7th of...

's method, it is exponentially faster than the previous methods (however, its running time is still exponential in n).

Both Conway's and Jensen's versions of the transfer-matrix method involve counting the number of polyominoes that have a certain width. Computing the number for all widths gives the total number of polyominoes. The basic idea behind the method is that possible beginning rows are considered, and then to determine the minimum number of squares needed to complete the polyomino of the given width. Combined with the use of generating function

Generating function

In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...

s, this technique is able to count many polyominoes at once, thus enabling it to run many times faster than methods that have to generate every polyomino.

Although it has excellent running time, the tradeoff is that this algorithm uses exponential amounts of memory (many gigabyte

Gigabyte

The gigabyte is a multiple of the unit byte for digital information storage. The prefix giga means 109 in the International System of Units , therefore 1 gigabyte is...

s of memory are needed for n above 50), is much harder to program than the other methods, and can't currently be used to count free polyominoes.

Fixed polyominoes

Theoretical arguments and numerical calculations support the estimate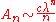

where

and

. However, this result is not proven and the values of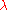

and c are only estimates.

The known theoretical results are not nearly as specific as this estimate. It has been proven that

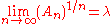
exists. In other words,

grows exponentially

Exponential growth

Exponential growth occurs when the growth rate of a mathematical function is proportional to the function's current value...

. The best known lower bound for

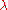is 3.980137. The best known upper bound, not improved since the 1970s, is

.

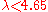To establish a lower bound, a simple but highly effective method is concatenation of polyominoes. Define the upper-right square to be the rightmost square in the uppermost row of the polyomino. Define the bottom-left square similarly. Then, the upper-right square of any polyomino of size n can be attached to the bottom-left square of any polyomino of size m to produce a unique (n+m)-omino. This proves

. Using this equation, one can show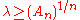

for all n. Refinements of this procedure combined with data for

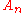produce the lower bound given above.

The upper bound is attained by generalizing the inductive method of enumerating polyominoes. Instead of adding one square at a time, one adds a cluster of squares at a time. This is often described as adding twigs. By proving that every n-omino is a sequence of twigs, and by proving limits on the combinations of possible twigs, one obtains an upper bound on the number of n-ominoes. For example, in the algorithm outlined above, at each step we must choose a larger number, and at most three new numbers are added (since at most three unnumbered squares are adjacent to any numbered square). This can be used to obtain an upper bound of 6.75. Using 2.8 million twigs, Klarner and Rivest

Ron Rivest

Ronald Linn Rivest is a cryptographer. He is the Andrew and Erna Viterbi Professor of Computer Science at MIT's Department of Electrical Engineering and Computer Science and a member of MIT's Computer Science and Artificial Intelligence Laboratory...

obtained an upper bound of 4.65.

Free polyominoes

Approximations for the number of fixed polyominoes and free polyominoes are related in a simple way. A free polyomino with no symmetries

Symmetry

Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...

(rotation or reflection) corresponds to 8 distinct fixed polyominoes, and for large n, most n-ominoes have no symmetries. Therefore, the number of fixed n-ominoes is approximately 8 times the number of free n-ominoes. Moreover, this approximation is exponentially more accurate as n increases.

Special classes of polyominoes

Exact formulas are known for enumerating polyominoes of special classes, such as the class of convex polyominoes and the class of directed polyominoes.

The definition of a convex polyomino is different from the usual definition of convexity

Convex set

In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...

. A polyomino is said to be column convex if its intersection with any vertical line is convex (in other words, each column has no holes). Similarly, a polyomino is said to be row convex if its intersection with any horizontal line is convex. A polyomino is said to be convex if it is row and column convex.

A polyomino is said to be directed if it contains a square, known as the root, such that every other square can be reached by movements of up or right one square, without leaving the polyomino.

Directed polyominoes, column (or row) convex polyominoes, and convex polyominoes have been effectively enumerated by area n, as well as by some other parameters such as perimeter, using generating function

Generating function

Uses of polyominoes

Polyominoes have fostered significant research in mathematics and are a fertile subject for logic puzzles and recreational mathematics

Recreational mathematics

Recreational mathematics is an umbrella term, referring to mathematical puzzles and mathematical games.Not all problems in this field require a knowledge of advanced mathematics, and thus, recreational mathematics often attracts the curiosity of non-mathematicians, and inspires their further study...

. Challenges are often posed for covering (tiling

Tessellation

A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...

) a prescribed region, or the entire plane, with polyominoes, or folding a polyomino to create other shapes. Gardner proposed several simple games with a set of free pentominoes and a chessboard.
Some variants of the Sudoku puzzle use
polyomino-shaped regions on the grid. The game Tetris

Tetris

Tetris is a puzzle video game originally designed and programmed by Alexey Pajitnov in the Soviet Union. It was released on June 6, 1984, while he was working for the Dorodnicyn Computing Centre of the Academy of Science of the USSR in Moscow, Russian Soviet Federative Socialist Republic...

is based on the seven one-sided tetrominoes, and the board game Blokus

Blokus

Blokus is an abstract strategy board game for two to four players, invented by Bernard Tavitian and first released in 2000 by Sekkoïa, a French company. It has won several awards, including the Mensa Select award and the 2004 Teacher's Choice Award....

uses all of the free polyominoes up to pentominoes.

Tiling regions with sets of polyominoes

Puzzles commonly ask for tiling a given region with a given set of polyominoes, such as the 12 pentominoes. Golomb's and Gardner's books have many examples. A typical puzzle is to tile a 6×10 rectangle with the twelve pentominoes; the 2339 solutions to this were found in 1960. Where multiple copies of the polyominoes in the set are allowed, Golomb defines a hierarchy of different regions that a set may be able to tile, such as rectangles, strips, and the whole plane, and shows that whether polyominoes from a given set can tile the plane is undecidable

Recursive set

In computability theory, a set of natural numbers is called recursive, computable or decidable if there is an algorithm which terminates after a finite amount of time and correctly decides whether or not a given number belongs to the set....

, by mapping sets of Wang tile

Wang tile

Wang tiles , first proposed by mathematician, logician, and philosopher Hao Wang in 1961, are a class of formal systems...

s to sets of polyominoes.

Tiling regions with copies of a single polyomino

Another class of problems asks whether copies of a given polyomino can tile a rectangle

Rectangle

In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...

, and if so, what rectangles they can tile. These problems have been extensively studied for particular polyominoes, and tables of results for individual polyominoes are available. Klarner and Göbel showed that for any polyomino there is a finite set of prime rectangles it tiles, such that all other rectangles it tiles can be tiled by those prime rectangles.

Beyond rectangles, Golomb gave his hierarchy for single polyominoes: a polyomino may tile a rectangle, a half strip, a bent strip, an enlarged copy of itself, a quadrant, a strip, a half plane, the whole plane, certain combinations, or none of these. There are certain implications among these, both obvious (for example, if a polyomino tiles the half plane then it tiles the whole plane) and less so (for example, if a polyomino tiles an enlarged copy of itself, then it tiles the quadrant). Polyominoes of orders up to 6 are characterised in this hierarchy (with the status of one hexomino, later found to tile a rectangle, unresolved at that time).

In 2001 Cristopher Moore and John Michael Robson showed that the problem of tiling one polyomino with copies of another is
NP-complete

NP-complete

In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...

Tiling the plane with copies of a single polyomino

Tiling the plane with copies of a single polyomino has also been much discussed. It was noted in 1965 that all polyominoes of orders 1 through 6 tile the plane, and then that all but four heptominoes will do so. It was then established by David Bird that all but 26 octominoes tile the plane. Rawsthorne found that all but 235 polyominoes of order 9 tile, and such results have been extended to higher orders by Rhoads (to order 14) and others. Polyominoes tiling the plane have been classified by the symmetries of their tilings and by the number of aspects (orientations) in which the tiles appear in them.

Tiling a common figure with various polyominoes

The compatibility problem is to take two or more polyominoes and find a figure that can be tiled with each. Polyomino compatibility has been widely studied since the 1990s. Jorge Luis Mireles and Giovanni Resta have published websites of systematic results, and Livio Zucca shows results for some complicated cases like three different pentominoes. The general problem can be hard. The first compatibility figure for the L and X pentominoes was published in 2005 and had 80 tiles of each kind. Many pairs of polyominoes have been proved incompatible by systematic exhaustion. No algorithm is known for deciding whether two arbitrary polyominoes are compatible.

Etymology

The word polyomino and the names of the various orders of polyomino are all back-formations from the word domino, a common game piece consisting of two squares, with the first letter d- fancifully interpreted as a version of the prefix di- meaning “two”. The name domino for the game piece is believed to come from the spotted masquerade garment domino, from Latin dominus.

Most of the numerical prefix

Numerical prefix

Number prefixes are prefixes derived from numbers or numerals. In English and other European languages, they are used to coin numerous series of words, such as unicycle – bicycle – tricycle, dyad – triad – decade, biped – quadruped, September – October – November – December, decimal – hexadecimal,...

es are Greek. Polyominoes of order 9 and 11 more often take the Latin prefixes nona- (nonomino) and undeca- (undecomino) than the Greek prefixes ennea- (enneomino) and hendeca- (hendecomino).

External links

An interactive polyomino-tiling application
Karl Dahlke's polyomino finite-rectangle tilings
An implementation and description of Jensen's method
A paper describing modern estimates (PS)
MathPages – Notes on enumeration of polyominoes with various symmetries
List of dissection problems in Fairy Chess Review
Tetrads by Karl Scherer, Wolfram Demonstrations Project
Wolfram Demonstrations Project
The Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...

.

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.