
Wang tile
Encyclopedia
Formal system
In formal logic, a formal system consists of a formal language and a set of inference rules, used to derive an expression from one or more other premises that are antecedently supposed or derived . The axioms and rules may be called a deductive apparatus...
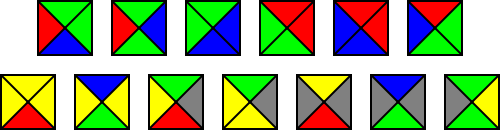
s. They are modelled visually by equal-sized squares with a color on each edge which can be arranged side by side (on a regular square grid) so that abutting edges of adjacent tiles have the same color; the tiles cannot be rotated or reflected.
The basic question about sets of Wang tiles is proving whether they can tile
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
the plane or not. This means that copies of the tiles can be arranged one by one to fill an infinite plane, without any grid position where no tile in the set can match the side colors of already laid out adjacent tiles.
In 1961, Wang presented an algorithm to take any finite set of tiles and decide whether they tiled the plane. In his purported proof of the correctness of the algorithm, he assumed that any set that could tile the plane would be able to tile the plane periodically (with a pattern that repeats, like standard wallpaper).
However, in 1966 Robert Berger
Robert Berger (mathematician)
Robert Berger is known for inventing the first aperiodic tiling using a set of 20,426 distinct tile shapes.The unexpected existence of aperiodic tilings, although not Berger's explicit construction of them, follows from another result proved by Berger: that the so-called domino problem is...
proved Wang's conjecture was wrong. He presented a set of Wang tiles that could only tile the plane aperiodically
Aperiodic tiling
An aperiodic tiling is a tiling obtained from an aperiodic set of tiles. Properly speaking, aperiodicity is a property of particular sets of tiles; any given finite tiling is either periodic or non-periodic...
. This meant it could fill the plane without holes, but the tiling couldn't be a simple repetition of a finite pattern. This is similar to a Penrose tiling
Penrose tiling
A Penrose tiling is a non-periodic tiling generated by an aperiodic set of prototiles named after Sir Roger Penrose, who investigated these sets in the 1970s. The aperiodicity of the Penrose prototiles implies that a shifted copy of a Penrose tiling will never match the original...
, or the arrangement of atoms in a quasicrystal
Quasicrystal
A quasiperiodic crystal, or, in short, quasicrystal, is a structure that is ordered but not periodic. A quasicrystalline pattern can continuously fill all available space, but it lacks translational symmetry...
. Although Berger's original set contained 20,426 tiles, he hypothesized that smaller sets would work, including subsets of his set. In later years, increasingly smaller sets were found. For example, the set of 13 tiles given above is an aperiodic set published by Karel Culik, II, in 1996. It can tile the plane, but not periodically.
Wang's algorithm for determining whether a given set of tiles can tile the plane was not correct. In fact, no such algorithm can exist. It is possible to translate any Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
into a set of Wang tiles, such that the Wang tiles can tile the plane if and only if the Turing machine will never halt
Halting problem
In computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
. This problem is undecidable; therefore, the Wang tiling problem is also uncomputable. In a sense, Wang tiles have computational power equivalent to that of a Turing machine.
The fact that Wang's procedure cannot theoretically work for arbitrary large tile sets does not render it useless for practical purposes.
Wang tiles can be generalized in various ways, all of which are also undecidable in the above sense. For example, Wang cubes are equal-sized cubes with colored faces and side colors can be matched on any polygonal tessellation
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
.
Culik and Kari have demonstrated aperiodic sets of Wang cubes. Winfree et al. have demonstrated the feasibility of creating molecular "tiles" made from DNA
DNA
Deoxyribonucleic acid is a nucleic acid that contains the genetic instructions used in the development and functioning of all known living organisms . The DNA segments that carry this genetic information are called genes, but other DNA sequences have structural purposes, or are involved in...
(deoxyribonucleic acid) that can act as Wang tiles. Mittal et al. have shown that these tiles can also be composed of peptide nucleic acid (PNA), a stable artificial mimic of DNA.
Wang tiles have recently become a popular tool for procedural synthesis of textures, heightfields, and other large and nonrepeating bidimensional data sets; a small set of precomputed or hand-made source tiles can be assembled very cheaply without too obvious repetitions and without periodicity.
In this case, traditional aperiodic tilings would show their very regular structure; much less constrained sets that guarantee at least two tile choices for any two given side colors are common because tileability is easily ensured and each tile can be selected pseudorandomly.
Important papers about this new application include:
- Jos Stam (1997), Aperiodic Texture Mapping introduces the idea of using Wang tiles for texture variation, with a deterministic substitution system.
- Michael F. Cohen, Jonathan Shade, Stefan Hiller, Oliver Deussen (2003), Wang Tiles for Image and Texture Generation introduces stochastic tiling and is very popular.
- Li-Yi Wei (2004), "Tile-Based Texture Mapping on Graphics Hardware" applies Wang Tiles for real-time texturing on a GPU
- Johannes Kopf, Daniel Cohen-Or, Oliver Deussen, Dani Lischinski (2006), Recursive Wang Tiles for Real-Time Blue Noise shows advanced applications.
The short story Wang's Carpets, later expanded to the novel Diaspora
Diaspora (novel)
Diaspora, a hard science fiction novel by the Australian writer Greg Egan, first appeared in print in 1997.-Plot introduction:This novel's setting is a posthuman future, in which transhumanism long ago became the default philosophy embraced by the vast majority of human cultures.The novel began as...
, by Greg Egan
Greg Egan
Greg Egan is an Australian science fiction author.Egan published his first work in 1983. He specialises in hard science fiction stories with mathematical and quantum ontology themes, including the nature of consciousness...
, postulates a universe, complete with resident organisms and intelligent beings, embodied as Wang tiles implemented by patterns of complex molecules.

