
Halting problem
Encyclopedia
In computability theory
, the halting problem can be stated as follows: Given a description of a computer program
, decide whether the program finishes running or continues to run forever. This is equivalent to the problem of deciding, given a program and an input, whether the program will eventually halt when run with that input, or will run forever.
Alan Turing
proved in 1936 that a general algorithm
to solve the halting problem for all possible program-input pairs cannot exist. A key part of the proof was a mathematical definition of a computer and program, what became known as a Turing machine
; the halting problem is undecidable
over Turing machines. It is one of the first examples of a decision problem
.
Jack Copeland
(2004) attributes the actual term halting problem to Martin Davis
.
that is general enough to be equivalent to a Turing machine. The problem is to determine, given a program and an input to the program, whether the program will eventually halt when run with that input. In this abstract framework, there are no resource limitations on the amount of memory or time required for the program's execution; it can take arbitrarily long, and use arbitrarily much storage space, before halting. The question is simply whether the given program will ever halt on a particular input.
For example, in pseudocode
, the program
does not halt; rather, it goes on forever in an infinite loop
. On the other hand, the program
halts very quickly.
A more complex program might be harder to analyze. The program could be run for some fixed time. If the program does not halt, there is in general no way to know if the program will eventually halt or run forever. Turing proved there is no algorithm which can be applied to any arbitrary program and input to decide whether the program stops when run with that input.
. (Turing's proof went to press in May 1936, whereas Alonzo Church
's proof of the undecidability of a problem in the lambda calculus
had already been published in April 1936.) Subsequently, many other undecidable problems have been described; the typical method of proving a problem to be undecidable is with the technique of reduction
. To do this, it is sufficient to show that if a solution to the new problem were found, it could be used to decide an undecidable problem by transforming instances of the undecidable problem into instances of the new problem. Since we already know that no method can decide the old problem, no method can decide the new problem either. Often the new problem is reduced to solving the halting problem.
For example, one such consequence of the halting problem's undecidability is that there cannot be a general algorithm
that decides whether a given statement about natural number
s is true or not. The reason for this is that the proposition
stating that a certain algorithm will halt given a certain input can be converted into an equivalent statement about natural numbers. If we had an algorithm that could solve every statement about natural numbers, it could certainly solve this one; but that would determine whether the original program halts, which is impossible, since the halting problem is undecidable.
Rice's theorem
generalizes the theorem that the halting problem is unsolvable. It states that any non-trivial property of the partial function
that is implemented by a program is undecidable. (A partial function is a function which may not always produce a result, and so is used to model programs, which can either produce results or fail to halt.) For example, the property "halt for the input 0" is undecidable. Note that this theorem holds only for properties of the partial function implemented by the program; Rice's Theorem does not apply to properties of the program itself. For example, "halt on input 0 within 100 steps" is not a property of the partial function that is implemented by the program—it is a property of the program implementing the partial function and is very much decidable.
Gregory Chaitin
has defined a halting probability, represented by the symbol Ω, a type of real number that informally is said to represent the probability
that a randomly produced program halts. These numbers have the same Turing degree
as the halting problem. It is a normal
and transcendental number
which can be defined
but cannot be completely computed
. This means one can prove that there is no algorithm
which produces the digits of Ω, although its first few digits can be calculated in simple cases.
While Turing's proof shows that there can be no general method or algorithm to determine whether algorithms halt, individual instances of that problem may very well be susceptible to attack. Given a specific algorithm, one can often show that it must halt for any input, and in fact computer scientist
s often do just that as part of a correctness proof. But each proof has to be developed specifically for the algorithm at hand; there is no mechanical, general way to determine whether algorithms on a Turing machine halt. However, there are some heuristics that can be used in an automated fashion to attempt to construct a proof, which succeed frequently on typical programs. This field of research is known as automated termination analysis
.
Since the negative answer to the halting problem shows that there are problems that cannot be solved by a Turing machine, the Church–Turing thesis limits what can be accomplished by any machine that implements effective method
s. However, not all machines conceivable to human imagination are subject to the Church–Turing thesis (e.g. oracle machine
s are not). It is an open question whether there can be actual deterministic physical processes that, in the long run, elude simulation by a Turing machine, and in particular whether any such hypothetical process could usefully be harnessed in the form of a calculating machine (a hypercomputer) that could solve the halting problem for a Turing machine amongst other things. It is also an open question whether any such unknown physical processes are involved in the working of the human brain
, and whether humans can solve the halting problem.
represents the halting problem.
This set is recursively enumerable, which means there is a computable function that lists all of the pairs (i, x) it contains. However, the complement of this set is not recursively enumerable.
There are many equivalent formulations of the halting problem; any set whose Turing degree
equals that of the halting problem is such a formulation. Examples of such sets include:
that decides whether an arbitrary program i halts on arbitrary input x; that is, the following function h is not computable:
Here program i refers to the i th program in an enumeration
of all the programs of a fixed Turing-complete model of computation.
The proof proceeds by directly establishing that every total computable function with two arguments differs from the required function h. To this end, given any total computable binary function f, the following partial function
g is also computable by some program e: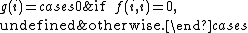
The verification that g is computable relies on the following constructs (or their equivalents):
The following pseudocode
illustrates a straightforward way to compute g:
Because g is partial computable, there must be a program e that computes g, by the assumption that the model of computation is Turing-complete. This program is one of all the programs on which the halting function h is defined. The next step of the proof shows that h(e,e) will not have the same value as f(e,e).
It follows from the definition of g that exactly one of the following two cases must hold:
In either case, f cannot be the same function as h. Because f was an arbitrary total computable function with two arguments, all such functions must differ from h.
This proof is analogous to Cantor's diagonal argument
. One may visualize a two-dimensional array with one column and one row for each natural number, as indicated in the table above. The value of f(i,j) is placed at column i, row j. Because f is assumed to be a total computable function, any element of the array can be calculated using f. The construction of the function g can be visualized using the main diagonal of this array. If the array has a 0 at position (i,i), then g(i) is 0. Otherwise, g(i) is undefined. The contradiction comes from the fact that there is some column e of the array corresponding to g itself. If f were the halting function h, there would be a 1 at position (e,e) if and only if g(e) is defined. But g is constructed so that g(e) is defined if and only if there is a 0 in position (e,e).
There are programs (interpreters
) that simulate the execution of whatever source code they are given. Such programs can demonstrate that a program does halt if this is the case: the interpreter itself will eventually halt its simulation, which shows that the original program halted. However, an interpreter will not halt if its input program does not halt, so this approach cannot solve the halting problem as stated. It does not successfully answer "doesn't halt" for programs that do not halt.
The halting problem is theoretically decidable for linear bounded automata
(LBAs) or deterministic machines with finite memory. A machine with finite memory has a finite number of states, and thus any deterministic program on it must eventually either halt or repeat a previous state:
Minsky warns us, however, that machines such as computers with e.g. a million small parts, each with two states, will have on the order of 21,000,000 possible states:
Minsky exhorts the reader to be suspicious—although a machine may be finite, and finite automata "have a number of theoretical limitations":
For more on this issue of "intractability" see Busy beaver
.
It can also be decided automatically whether a nondeterministic machine with finite memory halts on none of, some of, or all of the possible sequences of nondeterministic decisions, by enumerating states after each possible decision.
by introducing Turing machine
s. However, the result is in no way specific to them; it applies equally to any other model of computation
that is equivalent in its computational power to Turing machines, such as Markov algorithm
s, Lambda calculus
, Post systems, register machine
s, or tag systems.
What is important is that the formalization allows a straightforward mapping of algorithms to some data type
that the algorithm
can operate upon. For example, if the formalism
lets algorithms define functions over strings (such as Turing machines) then there should be a mapping of these algorithms to strings, and if the formalism lets algorithms define functions over natural numbers (such as computable function
s) then there should be a mapping of algorithms to natural numbers. The mapping to strings is usually the most straightforward, but strings over an alphabet
with n characters
can also be mapped to numbers by interpreting them as numbers in an n-ary numeral system
.
and sound
axiomatization of all statements about natural numbers is unachievable. The "sound" part is the weakening: it means that we require the axiomatic system in question to prove only true statements about natural numbers (it's very important to observe that the statement of the standard form of Gödel's First Incompleteness Theorem is completely unconcerned with the question of truth, and only concerns formal provability
).
The weaker form of the theorem can be proven from the undecidability of the halting problem as follows. Assume that we have a consistent and complete axiomatization of all true first-order logic
statements about natural number
s. Then we can build an algorithm that enumerates all these statements. This means that there is an algorithm N(n) that, given a natural number n, computes a true first-order logic statement about natural numbers such that, for all the true statements, there is at least one n such that N(n) yields that statement. Now suppose we want to decide if the algorithm with representation a halts on input i. By using Kleene's T predicate
, we can express the statement "a halts on input i" as a statement H(a, i) in the language of arithmetic. Since the axiomatization is complete it follows that either there is an n such that N(n) = H(a, i) or there is an n' such that N(n') = ¬ H(a, i). So if we iterate over all n until we either find H(a, i) or its negation, we will always halt. This means that this gives us an algorithm to decide the halting problem. Since we know that there cannot be such an algorithm, it follows that the assumption that there is a consistent and complete axiomatization of all true first-order logic statements about natural numbers must be false.
Suppose someone claims that program PHSR is a partial halting solver recognizer. Construct a program H:
input a program P
X := "input Q. if Q = P output 'halts' else loop forever"
run PHSR with X as input
If PHSR recognizes the constructed program X as a partial halting solver, that means that P, the only input for which X produces a result, halts. If PHSR fails to recognize X, then it must be because P does not halt. Therefore H can decide whether an arbitrary program P halts; it solves the halting problem. Since this is impossible, the program PHSR could not have been a partial halting solver recognizer as claimed. Therefore, no program can be a complete partial halting solver recognizer.
Another example, HT, of a Turing machine
which gives correct answers only for some instances of the halting problem can be described by the requirements that, if HT is started scanning a field which carries the first of a finite string of a consecutive "1"s, followed by one field with symbol "0" (i. e. a blank field), and followed in turn by a finite string of i consecutive "1"s, on an otherwise blank tape, then
While its existence has not been refuted (essentially: because there's no Turing machine which would halt only if started on a blank tape), such a Turing machine HT would solve the halting problem only partially either (because it doesn't necessarily scan the symbol "1" in the final state, if the Turing machine represented by a does halt when given the starting state and input represented by i, as explicit statements of the halting problem for Turing machines may require).
Computability theory (computer science)
Computability is the ability to solve a problem in an effective manner. It is a key topic of the field of computability theory within mathematical logic and the theory of computation within computer science...
, the halting problem can be stated as follows: Given a description of a computer program
Computer program
A computer program is a sequence of instructions written to perform a specified task with a computer. A computer requires programs to function, typically executing the program's instructions in a central processor. The program has an executable form that the computer can use directly to execute...
, decide whether the program finishes running or continues to run forever. This is equivalent to the problem of deciding, given a program and an input, whether the program will eventually halt when run with that input, or will run forever.
Alan Turing
Alan Turing
Alan Mathison Turing, OBE, FRS , was an English mathematician, logician, cryptanalyst, and computer scientist. He was highly influential in the development of computer science, providing a formalisation of the concepts of "algorithm" and "computation" with the Turing machine, which played a...
proved in 1936 that a general algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
to solve the halting problem for all possible program-input pairs cannot exist. A key part of the proof was a mathematical definition of a computer and program, what became known as a Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
; the halting problem is undecidable
Undecidable problem
In computability theory and computational complexity theory, an undecidable problem is a decision problem for which it is impossible to construct a single algorithm that always leads to a correct yes-or-no answer....
over Turing machines. It is one of the first examples of a decision problem
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
.
Jack Copeland
Jack Copeland
Brian Jack Copeland is Professor of Philosophy at the University of Canterbury, Christchurch, New Zealand.Copeland received a BPhil and DPhil from the University of Oxford in philosophy, where he undertook research on modal and non-classical logic.He is the Director of the Turing Archive for the...
(2004) attributes the actual term halting problem to Martin Davis
Martin Davis
Martin David Davis, is an American mathematician, known for his work on Hilbert's tenth problem . He received his Ph.D. from Princeton University in 1950, where his adviser was Alonzo Church . He is Professor Emeritus at New York University. He is the co-inventor of the Davis-Putnam and the DPLL...
.
Introduction
The halting problem is a decision problem about properties of computer programs on a fixed Turing-complete model of computation, i.e. all programs that can be written in some given programming languageProgramming language
A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
that is general enough to be equivalent to a Turing machine. The problem is to determine, given a program and an input to the program, whether the program will eventually halt when run with that input. In this abstract framework, there are no resource limitations on the amount of memory or time required for the program's execution; it can take arbitrarily long, and use arbitrarily much storage space, before halting. The question is simply whether the given program will ever halt on a particular input.
For example, in pseudocode
Pseudocode
In computer science and numerical computation, pseudocode is a compact and informal high-level description of the operating principle of a computer program or other algorithm. It uses the structural conventions of a programming language, but is intended for human reading rather than machine reading...
, the program
- while True: continue
does not halt; rather, it goes on forever in an infinite loop
Infinite loop
An infinite loop is a sequence of instructions in a computer program which loops endlessly, either due to the loop having no terminating condition, having one that can never be met, or one that causes the loop to start over...
. On the other hand, the program
- print "Hello World!"
halts very quickly.
A more complex program might be harder to analyze. The program could be run for some fixed time. If the program does not halt, there is in general no way to know if the program will eventually halt or run forever. Turing proved there is no algorithm which can be applied to any arbitrary program and input to decide whether the program stops when run with that input.
Importance and consequences
The halting problem is historically important because it was one of the first problems to be proved undecidableUndecidable problem
In computability theory and computational complexity theory, an undecidable problem is a decision problem for which it is impossible to construct a single algorithm that always leads to a correct yes-or-no answer....
. (Turing's proof went to press in May 1936, whereas Alonzo Church
Alonzo Church
Alonzo Church was an American mathematician and logician who made major contributions to mathematical logic and the foundations of theoretical computer science. He is best known for the lambda calculus, Church–Turing thesis, Frege–Church ontology, and the Church–Rosser theorem.-Life:Alonzo Church...
's proof of the undecidability of a problem in the lambda calculus
Lambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
had already been published in April 1936.) Subsequently, many other undecidable problems have been described; the typical method of proving a problem to be undecidable is with the technique of reduction
Reduction (complexity)
In computability theory and computational complexity theory, a reduction is a transformation of one problem into another problem. Depending on the transformation used this can be used to define complexity classes on a set of problems....
. To do this, it is sufficient to show that if a solution to the new problem were found, it could be used to decide an undecidable problem by transforming instances of the undecidable problem into instances of the new problem. Since we already know that no method can decide the old problem, no method can decide the new problem either. Often the new problem is reduced to solving the halting problem.
For example, one such consequence of the halting problem's undecidability is that there cannot be a general algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
that decides whether a given statement about natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s is true or not. The reason for this is that the proposition
Proposition
In logic and philosophy, the term proposition refers to either the "content" or "meaning" of a meaningful declarative sentence or the pattern of symbols, marks, or sounds that make up a meaningful declarative sentence...
stating that a certain algorithm will halt given a certain input can be converted into an equivalent statement about natural numbers. If we had an algorithm that could solve every statement about natural numbers, it could certainly solve this one; but that would determine whether the original program halts, which is impossible, since the halting problem is undecidable.
Rice's theorem
Rice's theorem
In computability theory, Rice's theorem states that, for any non-trivial property of partial functions, there is no general and effective method to decide whether an algorithm computes a partial function with that property...
generalizes the theorem that the halting problem is unsolvable. It states that any non-trivial property of the partial function
Partial function
In mathematics, a partial function from X to Y is a function ƒ: X' → Y, where X' is a subset of X. It generalizes the concept of a function by not forcing f to map every element of X to an element of Y . If X' = X, then ƒ is called a total function and is equivalent to a function...
that is implemented by a program is undecidable. (A partial function is a function which may not always produce a result, and so is used to model programs, which can either produce results or fail to halt.) For example, the property "halt for the input 0" is undecidable. Note that this theorem holds only for properties of the partial function implemented by the program; Rice's Theorem does not apply to properties of the program itself. For example, "halt on input 0 within 100 steps" is not a property of the partial function that is implemented by the program—it is a property of the program implementing the partial function and is very much decidable.
Gregory Chaitin
Gregory Chaitin
Gregory John Chaitin is an Argentine-American mathematician and computer scientist.-Mathematics and computer science:Beginning in 2009 Chaitin has worked on metabiology, a field parallel to biology dealing with the random evolution of artificial software instead of natural software .Beginning in...
has defined a halting probability, represented by the symbol Ω, a type of real number that informally is said to represent the probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
that a randomly produced program halts. These numbers have the same Turing degree
Turing degree
In computer science and mathematical logic the Turing degree or degree of unsolvability of a set of natural numbers measures the level of algorithmic unsolvability of the set...
as the halting problem. It is a normal
Normal number
In mathematics, a normal number is a real number whose infinite sequence of digits in every base b is distributed uniformly in the sense that each of the b digit values has the same natural density 1/b, also all possible b2 pairs of digits are equally likely with density b−2,...
and transcendental number
Transcendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
which can be defined
Definable number
A real number a is first-order definable in the language of set theory, without parameters, if there is a formula φ in the language of set theory, with one free variable, such that a is the unique real number such that φ holds in the standard model of set theory .For the purposes of this article,...
but cannot be completely computed
Computable number
In mathematics, particularly theoretical computer science and mathematical logic, the computable numbers, also known as the recursive numbers or the computable reals, are the real numbers that can be computed to within any desired precision by a finite, terminating algorithm...
. This means one can prove that there is no algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
which produces the digits of Ω, although its first few digits can be calculated in simple cases.
While Turing's proof shows that there can be no general method or algorithm to determine whether algorithms halt, individual instances of that problem may very well be susceptible to attack. Given a specific algorithm, one can often show that it must halt for any input, and in fact computer scientist
Computer scientist
A computer scientist is a scientist who has acquired knowledge of computer science, the study of the theoretical foundations of information and computation and their application in computer systems....
s often do just that as part of a correctness proof. But each proof has to be developed specifically for the algorithm at hand; there is no mechanical, general way to determine whether algorithms on a Turing machine halt. However, there are some heuristics that can be used in an automated fashion to attempt to construct a proof, which succeed frequently on typical programs. This field of research is known as automated termination analysis
Termination analysis
In computer science, a termination analysis is program analysis which attempts to determine whether the evaluation of a given program will definitely terminate. Because the halting problem is undecidable, termination analysis cannot work correctly in all cases. The aim is to find the answer...
.
Since the negative answer to the halting problem shows that there are problems that cannot be solved by a Turing machine, the Church–Turing thesis limits what can be accomplished by any machine that implements effective method
Effective method
In computability theory, an effective method is a procedure that reduces the solution of some class of problems to a series of rote steps which, if followed to the letter, and as far as may be necessary, is bound to:...
s. However, not all machines conceivable to human imagination are subject to the Church–Turing thesis (e.g. oracle machine
Oracle machine
In complexity theory and computability theory, an oracle machine is an abstract machine used to study decision problems. It can be visualized as a Turing machine with a black box, called an oracle, which is able to decide certain decision problems in a single operation. The problem can be of any...
s are not). It is an open question whether there can be actual deterministic physical processes that, in the long run, elude simulation by a Turing machine, and in particular whether any such hypothetical process could usefully be harnessed in the form of a calculating machine (a hypercomputer) that could solve the halting problem for a Turing machine amongst other things. It is also an open question whether any such unknown physical processes are involved in the working of the human brain
Human brain
The human brain has the same general structure as the brains of other mammals, but is over three times larger than the brain of a typical mammal with an equivalent body size. Estimates for the number of neurons in the human brain range from 80 to 120 billion...
, and whether humans can solve the halting problem.
Representing the halting problem as a set
The conventional representation of decision problems is the set of objects possessing the property in question. The halting set- K := { (i, x) | program i will eventually halt if run with input x}
represents the halting problem.
This set is recursively enumerable, which means there is a computable function that lists all of the pairs (i, x) it contains. However, the complement of this set is not recursively enumerable.
There are many equivalent formulations of the halting problem; any set whose Turing degree
Turing degree
In computer science and mathematical logic the Turing degree or degree of unsolvability of a set of natural numbers measures the level of algorithmic unsolvability of the set...
equals that of the halting problem is such a formulation. Examples of such sets include:
- { i | program i eventually halts when run with input 0 }
- { i | there is an input x such that program i eventually halts when run with input x }.
Sketch of proof
The proof shows there is no total computable functionComputable function
Computable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
that decides whether an arbitrary program i halts on arbitrary input x; that is, the following function h is not computable:

Here program i refers to the i th program in an enumeration
Enumeration
In mathematics and theoretical computer science, the broadest and most abstract definition of an enumeration of a set is an exact listing of all of its elements . The restrictions imposed on the type of list used depend on the branch of mathematics and the context in which one is working...
of all the programs of a fixed Turing-complete model of computation.
The proof proceeds by directly establishing that every total computable function with two arguments differs from the required function h. To this end, given any total computable binary function f, the following partial function
Partial function
In mathematics, a partial function from X to Y is a function ƒ: X' → Y, where X' is a subset of X. It generalizes the concept of a function by not forcing f to map every element of X to an element of Y . If X' = X, then ƒ is called a total function and is equivalent to a function...
g is also computable by some program e:
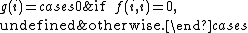
The verification that g is computable relies on the following constructs (or their equivalents):
- computable subprograms (the program that computes f is a subprogram in program e),
- duplication of values (program e computes the inputs i,i for f from the input i for g),
- conditional branching (program e selects between two results depending on the value it computes for f(i,i)),
- not producing a defined result (for example, by looping forever),
- returning a value of 0.
The following pseudocode
Pseudocode
In computer science and numerical computation, pseudocode is a compact and informal high-level description of the operating principle of a computer program or other algorithm. It uses the structural conventions of a programming language, but is intended for human reading rather than machine reading...
illustrates a straightforward way to compute g:
Because g is partial computable, there must be a program e that computes g, by the assumption that the model of computation is Turing-complete. This program is one of all the programs on which the halting function h is defined. The next step of the proof shows that h(e,e) will not have the same value as f(e,e).
It follows from the definition of g that exactly one of the following two cases must hold:
- g(e) = f(e,e) = 0. In this case h(e,e) = 1, because program e halts on input e.
- g(e) is undefined and f(e,e) ≠ 0. In this case h(e,e) = 0, because program e does not halt on input e.
In either case, f cannot be the same function as h. Because f was an arbitrary total computable function with two arguments, all such functions must differ from h.
This proof is analogous to Cantor's diagonal argument
Cantor's diagonal argument
Cantor's diagonal argument, also called the diagonalisation argument, the diagonal slash argument or the diagonal method, was published in 1891 by Georg Cantor as a mathematical proof that there are infinite sets which cannot be put into one-to-one correspondence with the infinite set of natural...
. One may visualize a two-dimensional array with one column and one row for each natural number, as indicated in the table above. The value of f(i,j) is placed at column i, row j. Because f is assumed to be a total computable function, any element of the array can be calculated using f. The construction of the function g can be visualized using the main diagonal of this array. If the array has a 0 at position (i,i), then g(i) is 0. Otherwise, g(i) is undefined. The contradiction comes from the fact that there is some column e of the array corresponding to g itself. If f were the halting function h, there would be a 1 at position (e,e) if and only if g(e) is defined. But g is constructed so that g(e) is defined if and only if there is a 0 in position (e,e).
Common pitfalls
The difficulty in the halting problem lies in the requirement that the decision procedure must work for all programs and inputs. A particular program either halts on a given input or does not halt. Consider one algorithm that always answers "halts" and another that always answers "doesn't halt." For any specific program and input, one of these two algorithms answers correctly, even though nobody may know which one.There are programs (interpreters
Interpreter (computing)
In computer science, an interpreter normally means a computer program that executes, i.e. performs, instructions written in a programming language...
) that simulate the execution of whatever source code they are given. Such programs can demonstrate that a program does halt if this is the case: the interpreter itself will eventually halt its simulation, which shows that the original program halted. However, an interpreter will not halt if its input program does not halt, so this approach cannot solve the halting problem as stated. It does not successfully answer "doesn't halt" for programs that do not halt.
The halting problem is theoretically decidable for linear bounded automata
Linear bounded automaton
In computer science, a linear bounded automaton is a restricted form of nondeterministic Turing machine.-Operation:Linear bounded automata satisfy the following three conditions:...
(LBAs) or deterministic machines with finite memory. A machine with finite memory has a finite number of states, and thus any deterministic program on it must eventually either halt or repeat a previous state:
- "...any finite-state machine, if left completely to itself, will fall eventually into a perfectly periodic repetitive pattern. The duration of this repeating pattern cannot exceed the number of internal states of the machine..."(italics in original, Minsky 1967, p. 24)
Minsky warns us, however, that machines such as computers with e.g. a million small parts, each with two states, will have on the order of 21,000,000 possible states:
- "This is a 1 followed by about three hundred thousand zeroes ... Even if such a machine were to operate at the frequencies of cosmic rays, the aeons of galactic evolution would be as nothing compared to the time of a journey through such a cycle" (Minsky p. 25)
Minsky exhorts the reader to be suspicious—although a machine may be finite, and finite automata "have a number of theoretical limitations":
- "...the magnitudes involved should lead one to suspect that theorems and arguments based chiefly on the mere finiteness [of] the state diagram may not carry a great deal of significance" (ibid).
For more on this issue of "intractability" see Busy beaver
Busy beaver
In computability theory, a busy beaver is a Turing machine that attains the maximum "operational busyness" among all the Turing machines in a certain class...
.
It can also be decided automatically whether a nondeterministic machine with finite memory halts on none of, some of, or all of the possible sequences of nondeterministic decisions, by enumerating states after each possible decision.
Formalization of the halting problem
In his original proof Turing formalized the concept of algorithmAlgorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
by introducing Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
s. However, the result is in no way specific to them; it applies equally to any other model of computation
Computation
Computation is defined as any type of calculation. Also defined as use of computer technology in Information processing.Computation is a process following a well-defined model understood and expressed in an algorithm, protocol, network topology, etc...
that is equivalent in its computational power to Turing machines, such as Markov algorithm
Markov algorithm
In theoretical computer science, a Markov algorithm is a string rewriting system that uses grammar-like rules to operate on strings of symbols. Markov algorithms have been shown to be Turing-complete, which means that they are suitable as a general model of computation and can represent any...
s, Lambda calculus
Lambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
, Post systems, register machine
Register machine
In mathematical logic and theoretical computer science a register machine is a generic class of abstract machines used in a manner similar to a Turing machine...
s, or tag systems.
What is important is that the formalization allows a straightforward mapping of algorithms to some data type
Data type
In computer programming, a data type is a classification identifying one of various types of data, such as floating-point, integer, or Boolean, that determines the possible values for that type; the operations that can be done on values of that type; the meaning of the data; and the way values of...
that the algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
can operate upon. For example, if the formalism
Formalism (mathematics)
In foundations of mathematics, philosophy of mathematics, and philosophy of logic, formalism is a theory that holds that statements of mathematics and logic can be thought of as statements about the consequences of certain string manipulation rules....
lets algorithms define functions over strings (such as Turing machines) then there should be a mapping of these algorithms to strings, and if the formalism lets algorithms define functions over natural numbers (such as computable function
Computable function
Computable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
s) then there should be a mapping of algorithms to natural numbers. The mapping to strings is usually the most straightforward, but strings over an alphabet
Alphabet
An alphabet is a standard set of letters—basic written symbols or graphemes—each of which represents a phoneme in a spoken language, either as it exists now or as it was in the past. There are other systems, such as logographies, in which each character represents a word, morpheme, or semantic...
with n characters
Character (computing)
In computer and machine-based telecommunications terminology, a character is a unit of information that roughly corresponds to a grapheme, grapheme-like unit, or symbol, such as in an alphabet or syllabary in the written form of a natural language....
can also be mapped to numbers by interpreting them as numbers in an n-ary numeral system
Numeral system
A numeral system is a writing system for expressing numbers, that is a mathematical notation for representing numbers of a given set, using graphemes or symbols in a consistent manner....
.
Relationship with Gödel's incompleteness theorem
The concepts raised by Gödel's incompleteness theorems are very similar to those raised by the halting problem, and the proofs are quite similar. In fact, a weaker form of the First Incompleteness Theorem is an easy consequence of the undecidability of the halting problem. This weaker form differs from the standard statement of the incompleteness theorem by asserting that a complete, consistentConsistency proof
In logic, a consistent theory is one that does not contain a contradiction. The lack of contradiction can be defined in either semantic or syntactic terms. The semantic definition states that a theory is consistent if and only if it has a model, i.e. there exists an interpretation under which all...
and sound
Soundness
In mathematical logic, a logical system has the soundness property if and only if its inference rules prove only formulas that are valid with respect to its semantics. In most cases, this comes down to its rules having the property of preserving truth, but this is not the case in general. The word...
axiomatization of all statements about natural numbers is unachievable. The "sound" part is the weakening: it means that we require the axiomatic system in question to prove only true statements about natural numbers (it's very important to observe that the statement of the standard form of Gödel's First Incompleteness Theorem is completely unconcerned with the question of truth, and only concerns formal provability
Formal proof
A formal proof or derivation is a finite sequence of sentences each of which is an axiom or follows from the preceding sentences in the sequence by a rule of inference. The last sentence in the sequence is a theorem of a formal system...
).
The weaker form of the theorem can be proven from the undecidability of the halting problem as follows. Assume that we have a consistent and complete axiomatization of all true first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
statements about natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s. Then we can build an algorithm that enumerates all these statements. This means that there is an algorithm N(n) that, given a natural number n, computes a true first-order logic statement about natural numbers such that, for all the true statements, there is at least one n such that N(n) yields that statement. Now suppose we want to decide if the algorithm with representation a halts on input i. By using Kleene's T predicate
Kleene's T predicate
In computability theory, the T predicate, first studied by mathematician Stephen Cole Kleene, is a particular set of triples of natural numbers that is used to represent computable functions within formal theories of arithmetic...
, we can express the statement "a halts on input i" as a statement H(a, i) in the language of arithmetic. Since the axiomatization is complete it follows that either there is an n such that N(n) = H(a, i) or there is an n' such that N(n') = ¬ H(a, i). So if we iterate over all n until we either find H(a, i) or its negation, we will always halt. This means that this gives us an algorithm to decide the halting problem. Since we know that there cannot be such an algorithm, it follows that the assumption that there is a consistent and complete axiomatization of all true first-order logic statements about natural numbers must be false.
Recognizing partial solutions
There are many programs that either return a correct answer to the halting problem or do not return an answer at all. If it were possible to decide whether any given program gives only correct answers, one might hope to collect a large number of such programs and run them in parallel, in the hope of being able to determine whether any programs halt. Curiously, recognizing such partial halting solvers (PHS) is just as hard as the halting problem itself.Suppose someone claims that program PHSR is a partial halting solver recognizer. Construct a program H:
input a program P
X := "input Q. if Q = P output 'halts' else loop forever"
run PHSR with X as input
If PHSR recognizes the constructed program X as a partial halting solver, that means that P, the only input for which X produces a result, halts. If PHSR fails to recognize X, then it must be because P does not halt. Therefore H can decide whether an arbitrary program P halts; it solves the halting problem. Since this is impossible, the program PHSR could not have been a partial halting solver recognizer as claimed. Therefore, no program can be a complete partial halting solver recognizer.
Another example, HT, of a Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
which gives correct answers only for some instances of the halting problem can be described by the requirements that, if HT is started scanning a field which carries the first of a finite string of a consecutive "1"s, followed by one field with symbol "0" (i. e. a blank field), and followed in turn by a finite string of i consecutive "1"s, on an otherwise blank tape, then
- HT halts for any such starting state, i. e. for any input of finite positive integers a and i;
- HT halts on a completely blank tape if and only if the Turing machine represented by a does not halt when given the starting state and input represented by i; and
- HT halts on a nonblank tape, scanning an appropriate field (which however does not necessarily carry the symbol "1") if and only if the Turing machine represented by a does halt when given the starting state and input represented by i. In this case, the final state in which HT halted (contents of the tape, and field being scanned) shall be equal to some particular intermediate state which the Turing machine represented by a attains when given the starting state and input represented by i; or, if all those intermediate states (including the starting state represented by i) leave the tape blank, then the final state in which HT halted shall be scanning a "1" on an otherwise blank tape.
While its existence has not been refuted (essentially: because there's no Turing machine which would halt only if started on a blank tape), such a Turing machine HT would solve the halting problem only partially either (because it doesn't necessarily scan the symbol "1" in the final state, if the Turing machine represented by a does halt when given the starting state and input represented by i, as explicit statements of the halting problem for Turing machines may require).
History of the halting problem
- 1900 – David HilbertDavid HilbertDavid Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
poses his "23 questions" (now known as Hilbert's problemsHilbert's problemsHilbert's problems form a list of twenty-three problems in mathematics published by German mathematician David Hilbert in 1900. The problems were all unsolved at the time, and several of them were very influential for 20th century mathematics...
) at the Second International Congress of MathematiciansInternational Congress of MathematiciansThe International Congress of Mathematicians is the largest conference for the topic of mathematics. It meets once every four years, hosted by the International Mathematical Union ....
in Paris. "Of these, the second was that of proving the consistency of the 'Peano axiomsPeano axiomsIn mathematical logic, the Peano axioms, also known as the Dedekind–Peano axioms or the Peano postulates, are a set of axioms for the natural numbers presented by the 19th century Italian mathematician Giuseppe Peano...
' on which, as he had shown, the rigour of mathematics depended" (Hodges p. 83, Davis' commentary in Davis, 1965, p. 108). - 1920–1921 – Emil Post explores the halting problem for tag systems, regarding it as a candidate for unsolvability. (Source: Absolutely unsolvable problems and relatively undecidable propositions – account of an anticipation, in Davis, 1965, pp. 340–433.) Its unsolvability was not established until much later, by Marvin MinskyMarvin MinskyMarvin Lee Minsky is an American cognitive scientist in the field of artificial intelligence , co-founder of Massachusetts Institute of Technology's AI laboratory, and author of several texts on AI and philosophy.-Biography:...
[1961]. - 1928—Hilbert recasts his 'Second Problem' at the Bologna International Congress (cf Reid pp. 188–189). Hodges claims he posed three questions: i.e. #1: Was mathematics complete? #2: Was mathematics consistent? #3: Was mathematics decidable? (Hodges p. 91). The third question is known as the EntscheidungsproblemEntscheidungsproblemIn mathematics, the is a challenge posed by David Hilbert in 1928. The asks for an algorithm that will take as input a description of a formal language and a mathematical statement in the language and produce as output either "True" or "False" according to whether the statement is true or false...
(Decision Problem) (Hodges p. 91, Penrose p. 34) - 1930 – Kurt GödelKurt GödelKurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the...
announces a proof as an answer to the first two of Hilbert's 1928 questions [cf Reid p. 198]. "At first he [Hilbert] was only angry and frustrated, but then he began to try to deal constructively with the problem... Gödel himself felt – and expressed the thought in his paper – that his work did not contradict Hilbert's formalistic point of view" (Reid p. 199). - 1931—Gödel publishes "On Formally Undecidable Propositions of Principia Mathematica and Related Systems I", (reprinted in Davis, 1965, p. 5ff)
- 19 April 1935 – Alonzo ChurchAlonzo ChurchAlonzo Church was an American mathematician and logician who made major contributions to mathematical logic and the foundations of theoretical computer science. He is best known for the lambda calculus, Church–Turing thesis, Frege–Church ontology, and the Church–Rosser theorem.-Life:Alonzo Church...
publishes "An Unsolvable Problem of Elementary Number Theory", wherein he identifies what it means for a function to be effectively calculable. Such a function will have an algorithm, and "...the fact that the algorithm has terminated becomes effectively known ..." (italics added, Davis, 1965, p. 100). - 1936—Church publishes the first proof that the Entscheidungsproblem is unsolvable [A Note on the Entscheidungsproblem, reprinted in Davis, 1965, p. 110].
- 7 October 1936 – Emil Post's paper "Finite Combinatory Processes. Formulation I" is received. Post adds to his "process" an instruction "(C) Stop". He called such a process "type 1 ... if the process it determines terminates for each specific problem." (Davis, 1965, p. 289ff)
- 1937 – Alan TuringAlan TuringAlan Mathison Turing, OBE, FRS , was an English mathematician, logician, cryptanalyst, and computer scientist. He was highly influential in the development of computer science, providing a formalisation of the concepts of "algorithm" and "computation" with the Turing machine, which played a...
's paper On Computable Numbers With an Application to the Entscheidungsproblem reaches print in January 1937 (reprinted in Davis, 1965, p. 115). Turing's proof departs from calculation by recursive functionsComputable functionComputable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
and introduces the notion of computation by machine. Stephen Kleene (1952) refers to this as one of the "first examples of decision problems proved unsolvable". - 1939 – J. Barkley Rosser observes the essential equivalence of "effective method" defined by Gödel, Church, and Turing (Rosser in Davis, 1965, p. 273, "Informal Exposition of Proofs of Gödel's Theorem and Church's Theorem").
- 1943—In a paper, Stephen Kleene states that "In setting up a complete algorithmic theory, what we do is describe a procedure ... which procedure necessarily terminates and in such manner that from the outcome we can read a definite answer, 'Yes' or 'No,' to the question, 'Is the predicate value true?'."
- 1952—Kleene (1952) Chapter XIII ("Computable Functions") includes a discussion of the unsolvability of the halting problem for Turing machines and reformulates it in terms of machines that "eventually stop", i.e. halt: "... there is no algorithm for deciding whether any given machine, when started from any given situation, eventually stops." (Kleene (1952) p.382)
- 1952 – "Davis [ Martin DavisMartin DavisMartin David Davis, is an American mathematician, known for his work on Hilbert's tenth problem . He received his Ph.D. from Princeton University in 1950, where his adviser was Alonzo Church . He is Professor Emeritus at New York University. He is the co-inventor of the Davis-Putnam and the DPLL...
] thinks it likely that he first used the term 'halting problem' in a series of lectures that he gave at the Control Systems Laboratory at the University of Illinois in 1952 (letter from Davis to Copeland, 12 Dec. 2001.)" (Footnote 61 in Copeland (2004) pp.40ff)
External links
- Scooping the loop snooper - a poetic proof of undecidability of the halting problem

