
Computable function
Encyclopedia
Computable functions are the basic objects of study in computability theory
. Computable functions are the formalized analogue of the intuitive notion of algorithm
. They are used to discuss computability without referring to any concrete model of computation
such as Turing machine
s or register machine
s. Any definition, however, must make reference to some specific model of computation but all valid definitions yield the same class of functions.
Particular models of computability that give rise to the set of computable functions are the Turing-computable functions and the μ-recursive functions.
Before the precise definition of computable function, mathematician
s often used the informal term effectively calculable. This term has since come to be identified with the computable functions. Note that the effective computability of these functions does not imply that they can be efficiently computed (i.e. computed within a reasonable amount of time). In fact, for some effectively calculable functions it can be shown that any algorithm that computes them will be very inefficient in the sense that the running time of the algorithm increases exponentially
(or even superexponentially
) with the length of the input. The fields of feasible computability and computational complexity
study functions that can be computed efficiently.
According to the Church-Turing thesis, computable functions are exactly the functions that can be calculated using a mechanical calculation device given unlimited amounts of time and storage space. Equivalently, this thesis states that any function which has an algorithm is computable. Note that an algorithm in this sense is understood to be a sequence of steps a person with unlimited time and an infinite supply of pen and paper could follow.
The Blum axioms
can be used to define an abstract computational complexity theory
on the set of computable functions. In computational complexity theory, the problem of determining the complexity of a computable function is known as a function problem
.
, including
Although those models use different representations for the functions, their inputs and their outputs, translations exist between any two models. In the remainder of this article, functions from natural numbers to natural numbers are used (as is the case for, e.g., the μ-recursive functions).
Each computable function takes a fixed, finite number of natural numbers as arguments. Because the functions are partial
in general, they may not be defined for every possible choice of input. If a computable function is defined for a certain input, then it returns a single natural number as output (this output can be interpreted as a list of numbers using a pairing function
). These functions are also called partial recursive functions. In computability theory, the domain
of a function is taken to be the set of all inputs for which the function is defined.
A function which is defined for all possible arguments is called total. If a computable function is total, it is called a total computable function or total recursive function.
The notation indicates that the partial function is defined on arguments , and the notation indicates that is defined on the arguments and the value returned is . The case that a function is undefined for arguments is denoted by .
) telling how to compute the function. The models of computation listed above give different interpretations of what a procedure is and how it is used, but these interpretations share many properties. The fact that these models give equivalent classes of computable functions stems from the fact that each model is capable of reading and mimicking a procedure for any of the other models, much as a compiler
is able to read instructions in one computer language and emit instructions in another language.
Enderton [1977] gives the following characteristics of a procedure for computing a computable function; similar characterizations have been given by Turing [1936], Rogers [1967], and others.
Thus every computable function must have a finite program that completely describes how the function is to be computed. It is possible to compute the function by just following the instructions; no guessing or special insight is required.
Intuitively, the procedure proceeds step by step, with a specific rule to cover what to do at each step of the calculation. Only finitely many steps can be carried out before the value of the function is returned.
Thus if a value for f(x) is ever found, it must be the correct value. It is not necessary for the computing agent to distinguish correct outcomes from incorrect ones because the procedure is always correct when it produces an outcome.
Enderton goes on to list several clarifications of these requirements of the procedure for a computable function:
The field of computational complexity
studies functions with prescribed bounds on the time and/or space allowed in a successful computation.
A set of natural numbers is called computably enumerable (synonyms: recursively enumerable, semidecidable) if there is a computable function such that for each number , is defined if and only if
is in the set. Thus a set is computably enumerable if and only if it is the domain of some computable function. The word enumerable is used because the following are equivalent for a nonempty subset of the natural numbers: is the domain of a computable function. is the range of a total computable function. If is infinite then the function can be assumed to be injective.
If a set is the range of a function then the function can be viewed as an
enumeration of , because the list will include every element of .
Because each finitary relation on the natural numbers can be identified with a corresponding set of finite sequences of natural numbers, the notions of computable relation and computably enumerable relation can be defined from their analogues for sets.
, it is common to consider formal language
s. An alphabet is an arbitrary set. A word on an alphabet is a finite sequence of symbols from the alphabet; the same symbol may be used more than once. For example, binary strings are exactly the words on the alphabet . A language is a subset of the collection of all words on a fixed alphabet. For example, the collection of all binary strings that contain exactly 3 ones is a language over the binary alphabet.
A key property of a formal language is the level of difficulty required to decide whether a given word is in the language. Some coding system must be developed to allow a computable function to take an arbitrary word in the language as input; this is usually considered routine. A language is called computable (synonyms: recursive, decidable) if there is a computable function such that for each word over the alphabet, if the word is in the language and if the word is not in the language. Thus a language is computable just in case there is a procedure that is able to correctly tell whether arbitrary words are in the language.
A language is computably enumerable (synonyms: recursively enumerable, semidecidable) if there is a computable function such that is defined if and only if the word is in the language. The term enumerable has the same etymology as in computably enumerable sets of natural numbers.
If f and g are computable, then so are: f + g, f * g
,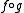
if
f is unary
, max(f,g), min(f,g), arg max{y≤f(x)} and many more combinations.
The following examples illustrate that a function may be computable though it is not known which algorithm computes it.
The Church-Turing thesis is sometimes used in proofs to justify that a particular function is computable by giving a concrete description of a procedure for the computation. This is permitted because it is believed that all such uses of the thesis can be removed by the tedious process of writing a formal procedure for the function in some model of computation.
The real numbers are uncountable so most real numbers are not computable. See computable number. The set of finitary
functions on the natural numbers is uncountable so most are not computable. Concrete examples of such functions are Busy beaver
, Kolmogorov complexity
, or any function that outputs the digits of noncomputable number, such as Chaitin's constant
.
Similarly, most subsets of the natural numbers are not computable. The Halting problem
was the first such set to be constructed. The Entscheidungsproblem
, proposed by David Hilbert
, asked whether there is an effective procedure to determine which mathematical statements (coded as natural numbers) are true. Turing and Church independently showed in the 1930s that this set of natural numbers is not computable. According to the Church-Turing thesis, there is no effective procedure (with an algorithm) which can perform these computations.
s A. A function f is defined to be computable in A (equivalently A-computable or computable relative to A) when it satisfies the definition of a computable function with modifications allowing access to A as an oracle. As with the concept of a computable function relative computability can be given equivalent definitions in many different models of computation. This is commonly accomplished by supplementing the model of computation with an additional primitive operation which asks whether a given integer is a member of A. We can also talk about f being computable in g by identifying g with its graph.
studies those sets that can be computed from a computable ordinal number of iterates of the Turing jump
of the empty set. This is equivalent to sets defined by both a universal and existential formula in the language of second order arithmetic and to some models of Hypercomputation
. Even more general recursion theories have been studied, such as E-recursion theory in which any set can be used as an argument to an E-recursive function.
studies models of computation that go beyond normal Turing computation. These don't violate the Church-Turing thesis since they allow operations that, whether or not they can be implemented in a physical device, couldn't be performed by a human working with pencil and paper.
Recursion theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
. Computable functions are the formalized analogue of the intuitive notion of algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
. They are used to discuss computability without referring to any concrete model of computation
Model of computation
In computability theory and computational complexity theory, a model of computation is the definition of the set of allowable operations used in computation and their respective costs...
such as Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
s or register machine
Register machine
In mathematical logic and theoretical computer science a register machine is a generic class of abstract machines used in a manner similar to a Turing machine...
s. Any definition, however, must make reference to some specific model of computation but all valid definitions yield the same class of functions.
Particular models of computability that give rise to the set of computable functions are the Turing-computable functions and the μ-recursive functions.
Before the precise definition of computable function, mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
s often used the informal term effectively calculable. This term has since come to be identified with the computable functions. Note that the effective computability of these functions does not imply that they can be efficiently computed (i.e. computed within a reasonable amount of time). In fact, for some effectively calculable functions it can be shown that any algorithm that computes them will be very inefficient in the sense that the running time of the algorithm increases exponentially
Exponential growth
Exponential growth occurs when the growth rate of a mathematical function is proportional to the function's current value...
(or even superexponentially
Tetration
In mathematics, tetration is an iterated exponential and is the next hyper operator after exponentiation. The word tetration was coined by English mathematician Reuben Louis Goodstein from tetra- and iteration. Tetration is used for the notation of very large numbers...
) with the length of the input. The fields of feasible computability and computational complexity
Computational Complexity
Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...
study functions that can be computed efficiently.
According to the Church-Turing thesis, computable functions are exactly the functions that can be calculated using a mechanical calculation device given unlimited amounts of time and storage space. Equivalently, this thesis states that any function which has an algorithm is computable. Note that an algorithm in this sense is understood to be a sequence of steps a person with unlimited time and an infinite supply of pen and paper could follow.
The Blum axioms
Blum axioms
In computational complexity theory the Blum axioms or Blum complexity axioms are axioms which specify desirable properties of complexity measures on the set of computable functions. The axioms were first defined by Manuel Blum in 1967....
can be used to define an abstract computational complexity theory
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
on the set of computable functions. In computational complexity theory, the problem of determining the complexity of a computable function is known as a function problem
Function problem
In computational complexity theory, a function problem is a computational problem where a single output is expected for every input, but the output is more complex than that of a decision problem, that is, it isn't just YES or NO...
.
Definition
The class of computable functions can be defined in many equivalent models of computationModel of computation
In computability theory and computational complexity theory, a model of computation is the definition of the set of allowable operations used in computation and their respective costs...
, including
- Turing machineTuring machineA Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
s - μ-recursive functions
- Lambda calculusLambda calculusIn mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
- Post machines (Post-Turing machinePost-Turing machineA Post–Turing machine is a "program formulation" of an especially simple type of Turing machine, comprising a variant of Emil Post's Turing-equivalent model of computation described below. A Post–Turing machine is a "program formulation" of an especially simple type of Turing machine, comprising a...
s and tag machinesTag systemA tag system is a deterministic computational model published by Emil Leon Post in 1943 as a simple form of Post canonical system. A tag system may also be viewed as an abstract machine, called a Post tag machine —briefly, a finite state machine whose only tape is a FIFO queue of unbounded length,...
). - Register machineRegister machineIn mathematical logic and theoretical computer science a register machine is a generic class of abstract machines used in a manner similar to a Turing machine...
s
Although those models use different representations for the functions, their inputs and their outputs, translations exist between any two models. In the remainder of this article, functions from natural numbers to natural numbers are used (as is the case for, e.g., the μ-recursive functions).
Each computable function takes a fixed, finite number of natural numbers as arguments. Because the functions are partial
Partial function
In mathematics, a partial function from X to Y is a function ƒ: X' → Y, where X' is a subset of X. It generalizes the concept of a function by not forcing f to map every element of X to an element of Y . If X' = X, then ƒ is called a total function and is equivalent to a function...
in general, they may not be defined for every possible choice of input. If a computable function is defined for a certain input, then it returns a single natural number as output (this output can be interpreted as a list of numbers using a pairing function
Pairing function
In mathematics a pairing function is a process to uniquely encode two natural numbers into a single natural number.Any pairing function can be used in set theory to prove that integers and rational numbers have the same cardinality as natural numbers...
). These functions are also called partial recursive functions. In computability theory, the domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
of a function is taken to be the set of all inputs for which the function is defined.
A function which is defined for all possible arguments is called total. If a computable function is total, it is called a total computable function or total recursive function.
The notation indicates that the partial function is defined on arguments , and the notation indicates that is defined on the arguments and the value returned is . The case that a function is undefined for arguments is denoted by .
Characteristics of computable functions
The basic characteristic of a computable function is that there must be a finite procedure (an algorithmAlgorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
) telling how to compute the function. The models of computation listed above give different interpretations of what a procedure is and how it is used, but these interpretations share many properties. The fact that these models give equivalent classes of computable functions stems from the fact that each model is capable of reading and mimicking a procedure for any of the other models, much as a compiler
Compiler
A compiler is a computer program that transforms source code written in a programming language into another computer language...
is able to read instructions in one computer language and emit instructions in another language.
Enderton [1977] gives the following characteristics of a procedure for computing a computable function; similar characterizations have been given by Turing [1936], Rogers [1967], and others.
- “There must be exact instructions (i.e. a program), finite in length, for the procedure.”
Thus every computable function must have a finite program that completely describes how the function is to be computed. It is possible to compute the function by just following the instructions; no guessing or special insight is required.
- “If the procedure is given a k-tuple x in the domain of f, then after a finite number of discrete steps the procedure must terminate and produce f(x).”
Intuitively, the procedure proceeds step by step, with a specific rule to cover what to do at each step of the calculation. Only finitely many steps can be carried out before the value of the function is returned.
- “If the procedure is given a k-tuple x which is not in the domain of f, then the procedure might go on forever, never halting. Or it might get stuck at some point, but it must not pretend to produce a value for f at x.”
Thus if a value for f(x) is ever found, it must be the correct value. It is not necessary for the computing agent to distinguish correct outcomes from incorrect ones because the procedure is always correct when it produces an outcome.
Enderton goes on to list several clarifications of these requirements of the procedure for a computable function:
- The procedure must theoretically work for arbitrarily large arguments. It is not assumed that the arguments are smaller than the number of atoms in the Earth, for example.
- The procedure is required to halt after finitely many steps in order to produce an output, but it may take arbitrarily many steps before halting. No time limitation is assumed.
- Although the procedure may use only a finite amount of storage space during a successful computation, there is no bound on the amount of space that is used. It is assumed that additional storage space can be given to the procedure whenever the procedure asks for it.
The field of computational complexity
Computational Complexity
Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...
studies functions with prescribed bounds on the time and/or space allowed in a successful computation.
Computable sets and relations
A set of natural numbers is called computable (synonyms: recursive, decidable) if there is a computable, total function such that for any natural number , if is in and if is not in .A set of natural numbers is called computably enumerable (synonyms: recursively enumerable, semidecidable) if there is a computable function such that for each number , is defined if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
is in the set. Thus a set is computably enumerable if and only if it is the domain of some computable function. The word enumerable is used because the following are equivalent for a nonempty subset of the natural numbers: is the domain of a computable function. is the range of a total computable function. If is infinite then the function can be assumed to be injective.
If a set is the range of a function then the function can be viewed as an
enumeration of , because the list will include every element of .
Because each finitary relation on the natural numbers can be identified with a corresponding set of finite sequences of natural numbers, the notions of computable relation and computably enumerable relation can be defined from their analogues for sets.
Formal languages
In computability theory in computer scienceComputability theory (computer science)
Computability is the ability to solve a problem in an effective manner. It is a key topic of the field of computability theory within mathematical logic and the theory of computation within computer science...
, it is common to consider formal language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
s. An alphabet is an arbitrary set. A word on an alphabet is a finite sequence of symbols from the alphabet; the same symbol may be used more than once. For example, binary strings are exactly the words on the alphabet . A language is a subset of the collection of all words on a fixed alphabet. For example, the collection of all binary strings that contain exactly 3 ones is a language over the binary alphabet.
A key property of a formal language is the level of difficulty required to decide whether a given word is in the language. Some coding system must be developed to allow a computable function to take an arbitrary word in the language as input; this is usually considered routine. A language is called computable (synonyms: recursive, decidable) if there is a computable function such that for each word over the alphabet, if the word is in the language and if the word is not in the language. Thus a language is computable just in case there is a procedure that is able to correctly tell whether arbitrary words are in the language.
A language is computably enumerable (synonyms: recursively enumerable, semidecidable) if there is a computable function such that is defined if and only if the word is in the language. The term enumerable has the same etymology as in computably enumerable sets of natural numbers.
Examples
The following functions are computable:- Each function with a finite domainDomain (mathematics)In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
; e.g., any finite sequence of natural numbers.
- Each constant functionConstant functionIn mathematics, a constant function is a function whose values do not vary and thus are constant. For example the function f = 4 is constant since f maps any value to 4...
f : Nk → N, f(n1,...nk) := n.
- AdditionAdditionAddition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
f : N²→ N, f(n1,n2) := n1 + n2
- The function which gives the list of prime factors of a number.
- The greatest common divisorGreatest common divisorIn mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
of two numbers is a computable function.
- Bézout's identityBézout's identityIn number theory, Bézout's identity for two integers a, b is an expressionwhere x and y are integers , such that d is a common divisor of a and b. Bézout's lemma states that such coefficients exist for every pair of nonzero integers...
, a linear Diophantine equationDiophantine equationIn mathematics, a Diophantine equation is an indeterminate polynomial equation that allows the variables to be integers only. Diophantine problems have fewer equations than unknown variables and involve finding integers that work correctly for all equations...
If f and g are computable, then so are: f + g, f * g
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
,
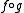
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
if
f is unary
Unary operation
In mathematics, a unary operation is an operation with only one operand, i.e. a single input. Specifically, it is a functionf:\ A\to Awhere A is a set. In this case f is called a unary operation on A....
, max(f,g), min(f,g), arg max{y≤f(x)} and many more combinations.
The following examples illustrate that a function may be computable though it is not known which algorithm computes it.
- The function f such that f(n) = 1 if there is a sequence of at least n consecutive fives in the decimal expansion of πPi' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
, and f(n) = 0 otherwise, is computable. (The function f is either the constant 1 function, which is computable, or else there is a k such that f(n) = 1 if n < k and f(n) = 0 if n ≥ k. Every such function is computable. It is not known whether there are arbitrarily long runs of fives in the decimal expansion of π, so we don't know which of those functions is f. Nevertheless, we know that the function f must be computable.)
- Each finite segment of an incomputable sequence of natural numbers (such as the Busy Beaver function Σ) is computable. E.g., for each natural number n, there exists an algorithm that computes the finite sequence Σ(0), Σ(1), Σ(2), ..., Σ(n) — in contrast to the fact that there is no algorithm that computes the entire Σ-sequence, i.e. Σ(n) for all n. Thus, "Print 0, 1, 4, 6, 13" is a trivial algorithm to compute Σ(0), Σ(1), Σ(2), Σ(3), Σ(4); similarly, for any given value of n, such a trivial algorithm exists (even though it may never be known or produced by anyone) to compute Σ(0), Σ(1), Σ(2), ..., Σ(n).
Church-Turing thesis
The Church-Turing thesis states that any function computable from a procedure possessing the three properties listed above is a computable function. Because these three properties are not formally stated, the Church-Turing thesis cannot be proved. The following facts are often taken as evidence for the thesis:- Many equivalent models of computation are known, and they all give the same definition of computable function (or a weaker version, in some instances).
- No stronger model of computation which is generally considered to be effectively calculable has been proposed.
The Church-Turing thesis is sometimes used in proofs to justify that a particular function is computable by giving a concrete description of a procedure for the computation. This is permitted because it is believed that all such uses of the thesis can be removed by the tedious process of writing a formal procedure for the function in some model of computation.
Incomputable functions and unsolvable problems
Every computable function has a finite procedure giving explicit, unambiguous instructions on how to compute it. Furthermore, this procedure has to be encoded in the finite alphabet used by the computational model, so there are only countably many computable functions. For example, functions may be encoded using a string of bits (the alphabet ).The real numbers are uncountable so most real numbers are not computable. See computable number. The set of finitary
Finitary
In mathematics or logic, a finitary operation is one, like those of arithmetic, that takes a finite number of input values to produce an output. An operation such as taking an integral of a function, in calculus, is defined in such a way as to depend on all the values of the function , and is so...
functions on the natural numbers is uncountable so most are not computable. Concrete examples of such functions are Busy beaver
Busy beaver
In computability theory, a busy beaver is a Turing machine that attains the maximum "operational busyness" among all the Turing machines in a certain class...
, Kolmogorov complexity
Kolmogorov complexity
In algorithmic information theory , the Kolmogorov complexity of an object, such as a piece of text, is a measure of the computational resources needed to specify the object...
, or any function that outputs the digits of noncomputable number, such as Chaitin's constant
Chaitin's constant
In the computer science subfield of algorithmic information theory, a Chaitin constant or halting probability is a real number that informally represents the probability that a randomly constructed program will halt...
.
Similarly, most subsets of the natural numbers are not computable. The Halting problem
Halting problem
In computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
was the first such set to be constructed. The Entscheidungsproblem
Entscheidungsproblem
In mathematics, the is a challenge posed by David Hilbert in 1928. The asks for an algorithm that will take as input a description of a formal language and a mathematical statement in the language and produce as output either "True" or "False" according to whether the statement is true or false...
, proposed by David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
, asked whether there is an effective procedure to determine which mathematical statements (coded as natural numbers) are true. Turing and Church independently showed in the 1930s that this set of natural numbers is not computable. According to the Church-Turing thesis, there is no effective procedure (with an algorithm) which can perform these computations.
Relative Computability
The notion of computability of a function can be relativized to an arbitrary set of natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s A. A function f is defined to be computable in A (equivalently A-computable or computable relative to A) when it satisfies the definition of a computable function with modifications allowing access to A as an oracle. As with the concept of a computable function relative computability can be given equivalent definitions in many different models of computation. This is commonly accomplished by supplementing the model of computation with an additional primitive operation which asks whether a given integer is a member of A. We can also talk about f being computable in g by identifying g with its graph.
Higher Recursion Theory
Hyperarithmetical theoryHyperarithmetical theory
In recursion theory, hyperarithmetic theory is a generalization of Turing computability. It has close connections with definability in second-order arithmetic and with weak systems of set theory such as Kripke–Platek set theory...
studies those sets that can be computed from a computable ordinal number of iterates of the Turing jump
Turing jump
In computability theory, the Turing jump or Turing jump operator, named for Alan Turing, is an operation that assigns to each decision problem a successively harder decision problem with the property that is not decidable by an oracle machine with an oracle for .The operator is called a jump...
of the empty set. This is equivalent to sets defined by both a universal and existential formula in the language of second order arithmetic and to some models of Hypercomputation
Hypercomputation
Hypercomputation or super-Turing computation refers to models of computation that are more powerful than, or are incomparable with, Turing computability. This includes various hypothetical methods for the computation of non-Turing-computable functions, following super-recursive algorithms...
. Even more general recursion theories have been studied, such as E-recursion theory in which any set can be used as an argument to an E-recursive function.
Hyper-computation
Although the Church-Turing thesis states that the computable functions include all functions with algorithms, it is possible to consider broader classes of functions that relax the requirements that algorithms must possess. The field of HypercomputationHypercomputation
Hypercomputation or super-Turing computation refers to models of computation that are more powerful than, or are incomparable with, Turing computability. This includes various hypothetical methods for the computation of non-Turing-computable functions, following super-recursive algorithms...
studies models of computation that go beyond normal Turing computation. These don't violate the Church-Turing thesis since they allow operations that, whether or not they can be implemented in a physical device, couldn't be performed by a human working with pencil and paper.
See also
- Computable numberComputable numberIn mathematics, particularly theoretical computer science and mathematical logic, the computable numbers, also known as the recursive numbers or the computable reals, are the real numbers that can be computed to within any desired precision by a finite, terminating algorithm...
- Effective methodEffective methodIn computability theory, an effective method is a procedure that reduces the solution of some class of problems to a series of rote steps which, if followed to the letter, and as far as may be necessary, is bound to:...
- Theory of computationTheory of computationIn theoretical computer science, the theory of computation is the branch that deals with whether and how efficiently problems can be solved on a model of computation, using an algorithm...
- Recursion theoryRecursion theoryComputability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
- Turing degreeTuring degreeIn computer science and mathematical logic the Turing degree or degree of unsolvability of a set of natural numbers measures the level of algorithmic unsolvability of the set...
- Arithmetical hierarchyArithmetical hierarchyIn mathematical logic, the arithmetical hierarchy, arithmetic hierarchy or Kleene-Mostowski hierarchy classifies certain sets based on the complexity of formulas that define them...
- HypercomputationHypercomputationHypercomputation or super-Turing computation refers to models of computation that are more powerful than, or are incomparable with, Turing computability. This includes various hypothetical methods for the computation of non-Turing-computable functions, following super-recursive algorithms...
- Super-recursive algorithmSuper-recursive algorithmIn computability theory, super-recursive algorithms are a generalization of ordinary algorithms that are more powerful, that is, compute more than Turing machines. The term was introduced by Mark Burgin, whose book "Super-recursive algorithms" develops their theory and presents several mathematical...
- Semicomputable function

