Computable number
Encyclopedia
In mathematics
, particularly theoretical computer science
and mathematical logic
, the computable numbers, also known as the recursive numbers or the computable reals, are the real numbers that can be computed to within any desired precision by a finite, terminating algorithm
. Equivalent definitions can be given using μ-recursive functions, Turing machines or λ-calculus as the formal representation of algorithms. The computable numbers form a real closed field
and can be used in the place of real numbers for many, but not all, mathematical purposes.
defines the numbers to be computed in a manner similar to those defined by Alan Turing
in 1936, i.e. as "sequences of digits interpreted as decimal fractions" between 0 and 1:
The key notions in the definition are (1) that some n is specified at the start, (2) for any n the computation only takes a finite number of steps, after which the machine produces the desired output and terminates.
An alternate form of (2) – the machine successively prints all n of the digits on its tape, halting after printing the nth – emphasizes Minsky's observation: (3) That by use of a Turing machine, a finite definition – in the form of the machine's table – is being used to define what is a potentially-infinite string of decimal digits.
This is however not the modern definition which only requires the result be accurate to within any given accuracy. The informal definition above is subject to a rounding problem called the table-maker's dilemma whereas the modern definition is not.
a is said to be computable if it can be approximated by some computable function
in the following manner: given any integer
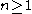, the function produces an integer k such that:
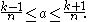
There are two similar definitions that are equivalent:
There is another equivalent definition of computable numbers via computable Dedekind cut
s. A computable Dedekind cut is a computable function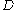
which when provided with a rational number 
as input returns 
or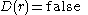 
, satisfying the following conditions: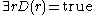
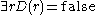
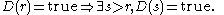
An example is given by a program D that defines the cube root of 3. Assuming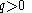
this is defined by: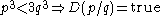
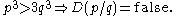
A real number is computable if and only if there is a computable Dedekind cut D converging to it. The function D is unique for each irrational computable number (although of course two different programs may provide the same function).
A complex number
is called computable if its real and imaginary parts are computable.
real numbers are not computable. The computable numbers can be counted by assigning a Gödel number
to each Turing machine definition. This gives a function from the naturals to the computable reals. Although the computable numbers are an ordered field, the set of Gödel numbers corresponding to computable numbers is not itself computably enumerable, because it is not possible to effectively determine which Gödel numbers correspond to Turing machines that produce computable reals. In order to produce a computable real, a Turing machine must compute a total function, but the corresponding decision problem
is in Turing degree
0′′. Thus Cantor's diagonal argument
cannot be used to produce uncountably many computable reals; at best, the reals formed from this method will be uncomputable.
The arithmetical operations on computable numbers are themselves computable in the sense that whenever real numbers a and b are computable then the following real numbers are also computable: a + b, a - b, ab, and a/b if b is nonzero.
These operations are actually uniformly computable; for example, there is a Turing machine which on input (A,B,
) produces output r, where A is the description of a Turing machine approximating a, B is the description of a Turing machine approximating b, and r is an 
approximation of a+b.
The computable real numbers do not share all the properties of the real numbers used in analysis. For example, the least upper bound of a bounded increasing computable sequence of computable real numbers need not be a computable real number (Bridges and Richman, 1987:58). A sequence with this property is known as a Specker sequence
, as the first construction is due to E. Specker (1949). Despite the existence of counterexamples such as these, parts of calculus and real analysis can be developed in the field of computable numbers, leading to the study of computable analysis
.
The order relation on the computable numbers is not computable. There is no Turing machine which on input A (the description of a Turing machine approximating the number
) outputs "YES" if 
and "NO" if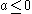 
. The reason: suppose the machine described by A keeps outputting 0 as 
approximations. It is not clear how long to wait before deciding that the machine will never output an approximation which forces a to be positive. Thus the machine will eventually have to guess that the number will equal 0, in order to produce an output; the sequence may later become different from 0. This idea can be used to show that the machine is incorrect on some sequences if it computes a total function. A similar problem occurs when the computable reals are represented as Dedekind cut
s. The same holds for the equality relation : the equality test is not computable.
While the full order relation is not computable, the restriction of it to pairs of unequal numbers is computable. That is, there is a program that takes an input two turing machines A and B approximating numbers a and b, where a≠b, and outputs whether a<b or a>b. It is sufficient to use ε-approximations where ε<|b-a|/2; so by taking increasingly small ε (with a limit to 0), one eventually can decide whether a<b or a>b.
Every computable number is definable
, but not vice versa. There are many definable, noncomputable real numbers, including:
A real number is computable if and only if the set of natural numbers it represents (when written in binary and viewed as a characteristic function) is computable.
(Note that the decimal expansion of a only refers to the digits following the decimal point.)
Turing was aware that this definition is equivalent to the
-approximation definition given above. The argument proceeds as follows: if a number is computable in the Turing sense, then it is also computable in the 
sense: if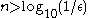 
, then the first n digits of the decimal expansion for a provide an 
approximation of a. For the converse, we pick an 
computable real number a and generate increasingly precisce approximations until the nth digit after the decimal point is certain. This always generates a decimal expansion equal to a but it may improperly end in an infinite sequence of 9's in which case it must have a finite (and thus computable) proper decimal expansion.
Unless certain topological properties of the real numbers are relevant it is often more convenient to deal with elements of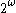
(total 0,1 valued functions) instead of reals numbers in 
. The members of 
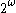can be identified with binary decimal expansions but since the decimal expansions 
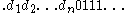and 
denote the same real number the inteveral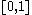 
can only be bijectively (and homeomorphically under the subset topology) identified with the subset of 
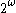not ending in all 1's.
Note that this property of decimal expansions means it's impossible to effectively identify computable real numbers defined in terms of a decimal expansion and those defined in the
approximation sense. Hirst has shown there is no algorithm which takes as input the description of a Turing machine which produces 
approximations for the computable number a, and produces as output a Turing machine which enumerates the digits of a in the sense of Turing's definition (see Hirst 2007). Similarly it means that the arithmetic operations on the computable reals are not effective on their decimal representations as when adding decimal numbers, in order to produce one digit it may be necessary to look arbitrarily far to the right to determine if there is a carry to the current location. This lack of uniformity is one reason that the contemporary definition of computable numbers uses 
approximations rather than decimal expansions.
However, from a computational or measure theoretic perspective the two structures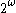
and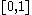 
are essentially identical. and computability theorists often refer to members of 
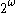as reals. While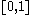 
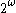is totally disconnected
for questions about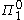
classes or randomness it's much less messy to work in 
.
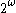Elements of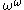
are sometimes called reals as well and though containing a homeomorphic image of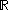 
in addition to being totally disconnected isn't even locally compact. This leads to genuine differences in the computational properties. For instance the 
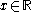satisfying 
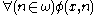with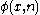 
quatifier free must be computable while the unique 
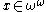satisfying a universal formula can be arbitrarily high in the hyperarithmetic hierarchy.
s, as well as e,
, and many other transcendental number
s. Though the computable reals exhaust those reals we can calculate or approximate, the assumption that all reals are computable leads to substantially different conclusions about the real numbers. The question naturally arises of whether it is possible to dispose of the full set of reals and use computable numbers for all of mathematics. This idea is appealing from a constructivist
point of view, and has been pursued by what Bishop
and Richman call the Russian school of constructive mathematics.
To actually develop analysis over computable numbers, some care must be taken. For example, if one uses the classical definition of a sequence, the set of computable numbers is not closed under the basic operation of taking the supremum
of a bounded sequence (for example, consider a Specker sequence
). This difficulty is addressed by considering only sequences which have a computable modulus of convergence
. The resulting mathematical theory is called computable analysis
.
representing the real numbers as programs computing approximations.
One example is the RealLib package (reallib home page).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, particularly theoretical computer science
Theoretical computer science
Theoretical computer science is a division or subset of general computer science and mathematics which focuses on more abstract or mathematical aspects of computing....
and mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, the computable numbers, also known as the recursive numbers or the computable reals, are the real numbers that can be computed to within any desired precision by a finite, terminating algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
. Equivalent definitions can be given using μ-recursive functions, Turing machines or λ-calculus as the formal representation of algorithms. The computable numbers form a real closed field
Real closed field
In mathematics, a real closed field is a field F that has the same first-order properties as the field of real numbers. Some examples are the field of real numbers, the field of real algebraic numbers, and the field of hyperreal numbers.-Definitions:...
and can be used in the place of real numbers for many, but not all, mathematical purposes.
Informal definition using a Turing machine as example
In the following, Marvin MinskyMarvin Minsky
Marvin Lee Minsky is an American cognitive scientist in the field of artificial intelligence , co-founder of Massachusetts Institute of Technology's AI laboratory, and author of several texts on AI and philosophy.-Biography:...
defines the numbers to be computed in a manner similar to those defined by Alan Turing
Alan Turing
Alan Mathison Turing, OBE, FRS , was an English mathematician, logician, cryptanalyst, and computer scientist. He was highly influential in the development of computer science, providing a formalisation of the concepts of "algorithm" and "computation" with the Turing machine, which played a...
in 1936, i.e. as "sequences of digits interpreted as decimal fractions" between 0 and 1:
- "A computable number [is] one for which there is a Turing machine which, given n on its initial tape, terminates with the nth digit of that number [encoded on its tape]." (Minsky 1967:159)
The key notions in the definition are (1) that some n is specified at the start, (2) for any n the computation only takes a finite number of steps, after which the machine produces the desired output and terminates.
An alternate form of (2) – the machine successively prints all n of the digits on its tape, halting after printing the nth – emphasizes Minsky's observation: (3) That by use of a Turing machine, a finite definition – in the form of the machine's table – is being used to define what is a potentially-infinite string of decimal digits.
This is however not the modern definition which only requires the result be accurate to within any given accuracy. The informal definition above is subject to a rounding problem called the table-maker's dilemma whereas the modern definition is not.
Formal definition
A real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
a is said to be computable if it can be approximated by some computable function
Computable function
Computable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
in the following manner: given any integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
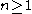, the function produces an integer k such that: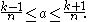There are two similar definitions that are equivalent:
- There exists a computable function which, given any positive rational error bound
, produces a rational numberRational numberIn mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
r such that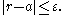
- There is a computable sequence of rational numbers
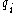converging to 
such that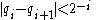 
for each i.
There is another equivalent definition of computable numbers via computable Dedekind cut
Dedekind cut
In mathematics, a Dedekind cut, named after Richard Dedekind, is a partition of the rationals into two non-empty parts A and B, such that all elements of A are less than all elements of B, and A contains no greatest element....
s. A computable Dedekind cut is a computable function
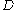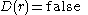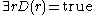
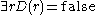
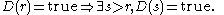
which when provided with a rational number as input returns or , satisfying the following conditions:An example is given by a program D that defines the cube root of 3. Assuming
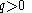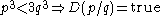
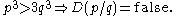
this is defined by:A real number is computable if and only if there is a computable Dedekind cut D converging to it. The function D is unique for each irrational computable number (although of course two different programs may provide the same function).
A complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
is called computable if its real and imaginary parts are computable.
Properties
While the set of real numbers is uncountable, the set of computable numbers is only countable and thus almost allAlmost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
real numbers are not computable. The computable numbers can be counted by assigning a Gödel number
Gödel number
In mathematical logic, a Gödel numbering is a function that assigns to each symbol and well-formed formula of some formal language a unique natural number, called its Gödel number. The concept was famously used by Kurt Gödel for the proof of his incompleteness theorems...
to each Turing machine definition. This gives a function from the naturals to the computable reals. Although the computable numbers are an ordered field, the set of Gödel numbers corresponding to computable numbers is not itself computably enumerable, because it is not possible to effectively determine which Gödel numbers correspond to Turing machines that produce computable reals. In order to produce a computable real, a Turing machine must compute a total function, but the corresponding decision problem
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
is in Turing degree
Turing degree
In computer science and mathematical logic the Turing degree or degree of unsolvability of a set of natural numbers measures the level of algorithmic unsolvability of the set...
0′′. Thus Cantor's diagonal argument
Cantor's diagonal argument
Cantor's diagonal argument, also called the diagonalisation argument, the diagonal slash argument or the diagonal method, was published in 1891 by Georg Cantor as a mathematical proof that there are infinite sets which cannot be put into one-to-one correspondence with the infinite set of natural...
cannot be used to produce uncountably many computable reals; at best, the reals formed from this method will be uncomputable.
The arithmetical operations on computable numbers are themselves computable in the sense that whenever real numbers a and b are computable then the following real numbers are also computable: a + b, a - b, ab, and a/b if b is nonzero.
These operations are actually uniformly computable; for example, there is a Turing machine which on input (A,B,
) produces output r, where A is the description of a Turing machine approximating a, B is the description of a Turing machine approximating b, and r is an approximation of a+b.The computable real numbers do not share all the properties of the real numbers used in analysis. For example, the least upper bound of a bounded increasing computable sequence of computable real numbers need not be a computable real number (Bridges and Richman, 1987:58). A sequence with this property is known as a Specker sequence
Specker sequence
In computability theory, a Specker sequence is a computable, strictly increasing, bounded sequence of rational numbers whose supremum is not a computable real number. The first example of such a sequence was constructed by Ernst Specker in 1949....
, as the first construction is due to E. Specker (1949). Despite the existence of counterexamples such as these, parts of calculus and real analysis can be developed in the field of computable numbers, leading to the study of computable analysis
Computable analysis
In mathematics, computable analysis is the study of which parts of real analysis and functional analysis can be carried out in a computable manner. It is closely related to constructive analysis.- Basic results :...
.
The order relation on the computable numbers is not computable. There is no Turing machine which on input A (the description of a Turing machine approximating the number
) outputs "YES" if and "NO" if 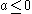. The reason: suppose the machine described by A keeps outputting 0 as approximations. It is not clear how long to wait before deciding that the machine will never output an approximation which forces a to be positive. Thus the machine will eventually have to guess that the number will equal 0, in order to produce an output; the sequence may later become different from 0. This idea can be used to show that the machine is incorrect on some sequences if it computes a total function. A similar problem occurs when the computable reals are represented as Dedekind cutDedekind cut
In mathematics, a Dedekind cut, named after Richard Dedekind, is a partition of the rationals into two non-empty parts A and B, such that all elements of A are less than all elements of B, and A contains no greatest element....
s. The same holds for the equality relation : the equality test is not computable.
While the full order relation is not computable, the restriction of it to pairs of unequal numbers is computable. That is, there is a program that takes an input two turing machines A and B approximating numbers a and b, where a≠b, and outputs whether a<b or a>b. It is sufficient to use ε-approximations where ε<|b-a|/2; so by taking increasingly small ε (with a limit to 0), one eventually can decide whether a<b or a>b.
Every computable number is definable
Definable number
A real number a is first-order definable in the language of set theory, without parameters, if there is a formula φ in the language of set theory, with one free variable, such that a is the unique real number such that φ holds in the standard model of set theory .For the purposes of this article,...
, but not vice versa. There are many definable, noncomputable real numbers, including:
- The binary representation of the Halting problemHalting problemIn computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
(or any other uncomputable set of natural numbers). - Chaitin's constantChaitin's constantIn the computer science subfield of algorithmic information theory, a Chaitin constant or halting probability is a real number that informally represents the probability that a randomly constructed program will halt...
,
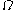, which is a type of real number that is Turing equivalent to the Halting problem.
A real number is computable if and only if the set of natural numbers it represents (when written in binary and viewed as a characteristic function) is computable.
Digit strings and the Cantor and Baire spaces
Turing's original paper defined computable numbers as follows:- A real number is computable if its digit sequence can be produced by some algorithm or Turing machine. The algorithm takes an integer
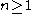as input and produces the 
-th digit of the real number's decimal expansion as output.
(Note that the decimal expansion of a only refers to the digits following the decimal point.)
Turing was aware that this definition is equivalent to the
-approximation definition given above. The argument proceeds as follows: if a number is computable in the Turing sense, then it is also computable in the sense: if 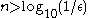, then the first n digits of the decimal expansion for a provide an approximation of a. For the converse, we pick an computable real number a and generate increasingly precisce approximations until the nth digit after the decimal point is certain. This always generates a decimal expansion equal to a but it may improperly end in an infinite sequence of 9's in which case it must have a finite (and thus computable) proper decimal expansion.Unless certain topological properties of the real numbers are relevant it is often more convenient to deal with elements of
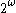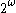(total 0,1 valued functions) instead of reals numbers in . The members of can be identified with binary decimal expansions but since the decimal expansions 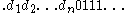and denote the same real number the inteveral 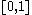can only be bijectively (and homeomorphically under the subset topology) identified with the subset of 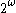not ending in all 1's.Note that this property of decimal expansions means it's impossible to effectively identify computable real numbers defined in terms of a decimal expansion and those defined in the
approximation sense. Hirst has shown there is no algorithm which takes as input the description of a Turing machine which produces approximations for the computable number a, and produces as output a Turing machine which enumerates the digits of a in the sense of Turing's definition (see Hirst 2007). Similarly it means that the arithmetic operations on the computable reals are not effective on their decimal representations as when adding decimal numbers, in order to produce one digit it may be necessary to look arbitrarily far to the right to determine if there is a carry to the current location. This lack of uniformity is one reason that the contemporary definition of computable numbers uses approximations rather than decimal expansions.However, from a computational or measure theoretic perspective the two structures
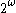and 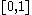are essentially identical. and computability theorists often refer to members of 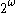as reals. While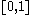 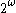is totally disconnectedTotally disconnected space
In topology and related branches of mathematics, a totally disconnected space is a topological space that is maximally disconnected, in the sense that it has no non-trivial connected subsets...
for questions about
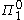classes or randomness it's much less messy to work in 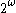.Elements of
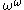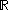
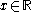are sometimes called reals as well and though containing a homeomorphic image of in addition to being totally disconnected isn't even locally compact. This leads to genuine differences in the computational properties. For instance the satisfying 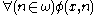with 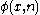quatifier free must be computable while the unique 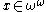satisfying a universal formula can be arbitrarily high in the hyperarithmetic hierarchy.Can computable numbers be used instead of the reals?
The computable numbers include many of the specific real numbers which appear in practice, including all algebraic numberAlgebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s, as well as e,
, and many other transcendental numberTranscendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
s. Though the computable reals exhaust those reals we can calculate or approximate, the assumption that all reals are computable leads to substantially different conclusions about the real numbers. The question naturally arises of whether it is possible to dispose of the full set of reals and use computable numbers for all of mathematics. This idea is appealing from a constructivist
Constructivism (mathematics)
In the philosophy of mathematics, constructivism asserts that it is necessary to find a mathematical object to prove that it exists. When one assumes that an object does not exist and derives a contradiction from that assumption, one still has not found the object and therefore not proved its...
point of view, and has been pursued by what Bishop
Errett Bishop
Errett Albert Bishop was an American mathematician known for his work on analysis. He is the father of constructive analysis, because of his 1967 Foundations of Constructive Analysis, where he proved most of the important theorems in real analysis by constructive methods.-Life:Errett Bishop's...
and Richman call the Russian school of constructive mathematics.
To actually develop analysis over computable numbers, some care must be taken. For example, if one uses the classical definition of a sequence, the set of computable numbers is not closed under the basic operation of taking the supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
of a bounded sequence (for example, consider a Specker sequence
Specker sequence
In computability theory, a Specker sequence is a computable, strictly increasing, bounded sequence of rational numbers whose supremum is not a computable real number. The first example of such a sequence was constructed by Ernst Specker in 1949....
). This difficulty is addressed by considering only sequences which have a computable modulus of convergence
Modulus of convergence
In real analysis, a branch of mathematics, a modulus of convergence is a function that tells how quickly a convergent sequence converges. These moduli are often employed in the study of computable analysis and constructive mathematics....
. The resulting mathematical theory is called computable analysis
Computable analysis
In mathematics, computable analysis is the study of which parts of real analysis and functional analysis can be carried out in a computable manner. It is closely related to constructive analysis.- Basic results :...
.
Implementation
There are some computer packages that work with computable real numbers,representing the real numbers as programs computing approximations.
One example is the RealLib package (reallib home page).