Dedekind cut - AbsoluteAstronomy.com

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, a Dedekind cut, named after Richard Dedekind

Richard Dedekind

Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...

, is a partition

Partition of a set

In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...

of the rationals

Rational number

In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...

into two non-empty parts A and B, such that all elements of A are less than all elements of B, and A contains no greatest element.

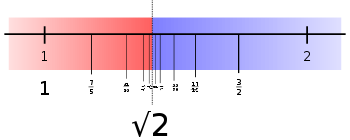
If B has a smallest element among the rationals, the cut corresponds to that rational. Otherwise, that cut defines a unique irrational number which, loosely speaking, fills the "gap" between A and B. In other words, A contains every rational number less than the cut, and B contains every rational number greater than the cut. An irrational cut is equated to an irrational number which is in neither set. Every real number, rational or not, is equated to one and only one cut of rationals.
More generally, a Dedekind cut is a partition of a totally ordered set into two non-empty parts, (A, B), such that A is closed downwards (meaning that for all a in A, x ≤ a implies that x is in A as well) and B is closed upwards, and A contains no greatest element. See also completeness (order theory)

Completeness (order theory)

In the mathematical area of order theory, completeness properties assert the existence of certain infima or suprema of a given partially ordered set . A special use of the term refers to complete partial orders or complete lattices...

.

In particular, as discussed below, we may consider Dedekind cuts among the real numbers defined as cuts among the rationals. It turns out that every cut of reals is identical to the cut produced by a specific real number (which can be identified as the smallest element of the B set). In other words, the number line

Number line

In basic mathematics, a number line is a picture of a straight line on which every point is assumed to correspond to a real number and every real number to a point. Often the integers are shown as specially-marked points evenly spaced on the line...

where every real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

is defined as a Dedekind cut of rationals is indeed a complete continuum

Linear continuum

In the mathematical field of order theory, a continuum or linear continuum is a generalization of the real line.Formally, a linear continuum is a linearly ordered set S of more than one element that is densely ordered, i.e., between any two members there is another, and which "lacks gaps" in the...

without any further gaps!

Dedekind used the word cut

Cut

Cut may refer to:* The act of cutting, the separation of an object into two through acutely directed force-Mathematics:* Cut * Branch cut, a concept in complex analysis* Dedekind cut, a partition of rational numbers* Cut-elimination theorem...

(Schnitt) in a visual sense rooted in Euclidean geometry. When two straight lines cross, one is said to cut the other. Dedekind's construction of the number line

Number line

ensures that two crossing lines always have one point in common because each of them defines a Dedekind cut on the other...

Representations

It is more symmetrical to use the (A,B) notation for Dedekind cuts, but each of A and B does determine the other. It can be a simplification, in terms of notation if nothing more, to concentrate on one 'half' — say, the lower one — and call any downward closed set A without greatest element

Greatest element

In mathematics, especially in order theory, the greatest element of a subset S of a partially ordered set is an element of S which is greater than or equal to any other element of S. The term least element is defined dually...

a "Dedekind cut".

If the ordered set S is complete, then, for every Dedekind cut (A, B) of S, the set B must have a minimal element b,
hence we must have that A is the interval

Interval (mathematics)

In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...

( −∞, b), and B the interval [b, +∞).
In this case, we say that b is represented by the cut (A,B).

The important purpose of the Dedekind cut is to work with number sets that are not complete. The cut itself can represent a number not in the original collection of numbers (most often rational number

Rational number

s). The cut can represent a number b, even though the numbers contained in the two sets A and B do not actually include the number b that their cut represents.

For example if A and B only contain rational numbers, they can still be cut at √2 by putting every negative rational number in A, along with every non-negative number whose square is less than 2; similarly B would contain every positive rational number whose square is greater than or equal to 2. Even though there is no rational value for √2, if the rational numbers are partitioned into A and B this way, the partition itself represents an irrational number

Irrational number

In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....

Ordering of cuts

Regard one Dedekind cut (A, B) as less than another Dedekind cut (C, D) if A is a proper subset of C. Equivalently, if D is a proper subset of B, the cut (A, B) is again less than (C, D). In this way, set inclusion can be used to represent the ordering of numbers, and all other relations (greater than, less than or equal to, equal to, and so on) can be similarly created from set relations.

The set of all Dedekind cuts is itself a linearly ordered set (of sets). Moreover, the set of Dedekind cuts has the least-upper-bound

Supremum

In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...

property, i.e., every nonempty subset of it that has any upper bound has a least upper bound. Thus, constructing the set of Dedekind cuts serves the purpose of embedding the original ordered set S, which might not have had the least-upper-bound property, within a (usually larger) linearly ordered set that does have this useful property.

Construction of the real numbers

A typical Dedekind cut of the rational number

Rational number

s is given by

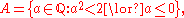
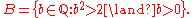
This cut represents the irrational number

Irrational number

In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....

√2 in Dedekind's construction. To truly establish this, one must show that this really is a cut and that it is the square root of two. However, neither claim is immediate. Showing that it is a cut requires showing that for any positive rational

with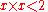

, there is a rational

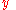with

and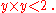

The choice

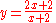works. Then we have a cut and it has a square no larger than 2, but to show equality requires showing that if

is any rational number less than 2, then there is positive

with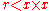

.

Note that the equality b² = 2 cannot hold since √2 is not rational.

Generalizations

A construction similar to Dedekind cuts is used for the construction of surreal number

Surreal number

In mathematics, the surreal number system is an arithmetic continuum containing the real numbers as well as infinite and infinitesimal numbers, respectively larger or smaller in absolute value than any positive real number...

Partially ordered sets

More generally, if S is a partially ordered set

Partially ordered set

In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...

, a completion of S means a complete lattice

Complete lattice

In mathematics, a complete lattice is a partially ordered set in which all subsets have both a supremum and an infimum . Complete lattices appear in many applications in mathematics and computer science...

L with an order-embedding of S into L. The notion of complete lattice generalizes the least-upper-bound property of the reals.

One completion of S is the set of its downwardly closed subsets, ordered by inclusion

Subset

In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...

. A related completion that preserves all existing sups and infs of S is obtained by the following construction: For each subset A of S, let A^u denote the set of upper bounds of A, and let A^l denote the set of lower bounds of A. (These operators form a Galois connection

Galois connection

In mathematics, especially in order theory, a Galois connection is a particular correspondence between two partially ordered sets . The same notion can also be defined on preordered sets or classes; this article presents the common case of posets. Galois connections generalize the correspondence...

.) Then the Dedekind–MacNeille completion

Dedekind–MacNeille completion

In order-theoretic mathematics, the Dedekind–MacNeille completion of a partially ordered set is the smallest complete lattice that contains the given partial order...

of S consists of all subsets A for which (A^u)^l = A; it is ordered by inclusion. The Dedekind-MacNeille completion is the smallest complete lattice with S embedded in it.

Allusions

In his chapter on Henri Bergson

Henri Bergson

Henri-Louis Bergson was a major French philosopher, influential especially in the first half of the 20th century. Bergson convinced many thinkers that immediate experience and intuition are more significant than rationalism and science for understanding reality.He was awarded the 1927 Nobel Prize...

, the author C.E.M. Joad employed imagery that was similar to Dedekind's concept of the cut. Joad was trying to explain how Bergson saw the mind as an instrument that projected permanent objects onto the experience of constant change. "The intellect, then, is a purely practical faculty, which has evolved for the purposes of action. What it does is to take the ceaseless, living flow of which the universe is composed and to make cuts across it, inserting artificial stops or gaps in what is really a continuous and indivisible process. The effect of these stops or gaps is to produce the impression of a world of apparently solid objects. These have no existence as separate objects in reality; they are, as it were, the design or pattern which our intellects have impressed on reality to serve our purposes." This is reminiscent of Dedekind's creation of a new irrational number at every gap in the continuous number line at which there is no existing real number.

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.