Gödel number
Encyclopedia
In mathematical logic
, a Gödel numbering is a function
that assigns to each symbol and well-formed formula
of some formal language
a unique natural number
, called its Gödel number. The concept was famously used by Kurt Gödel
for the proof of his incompleteness theorems
.
A Gödel numbering can be interpreted as an encoding
in which a number is assigned to each symbol
of a mathematical notation
, after which a sequence of natural number
s can then represent a sequence of strings. These sequences of natural numbers can again be represented by single natural numbers, facilitating their manipulation in formal theories of arithmetic.
Since Gödel's paper was published in 1931, the term "Gödel numbering" or "Gödel code" has been used to refer to more general assignments of natural numbers to mathematical objects.
In simple terms, we devise a method by which every formula or statement that can be formulated in our system gets a unique number, in such a way that we can mechanically convert back and forth between formulas and Gödel numbers. Clearly there are many ways this can be done. Given any statement, the number it is converted to is known as its Gödel number. A simple example is the way in which English is stored as a sequence of numbers in computers using ASCII
or Unicode
:
To encode an entire formula, which is a sequence of symbols, Gödel used the following system. Given a sequence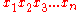
of positive integers, the Gödel encoding of the sequence is the product of the first n primes raised to their corresponding values in the sequence:
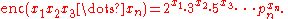
According to the fundamental theorem of arithmetic
, any number obtained in this way can be uniquely factored into prime factor
s, so it is possible to recover the original sequence from its Gödel number (for any given number n of symbols to be encoded).
Gödel specifically used this scheme at two levels: first, to encode sequences of symbols representing formulas, and second, to encode sequences of formulas representing proofs. This allowed him to show a correspondence between statements about natural numbers and statements about the provability of theorems about natural numbers, the key observation of the proof.
There are more sophisticated (and more concise) ways to construct a Gödel numbering for sequences
.
For example, supposing there are K basic symbols, an alternative Gödel numbering could be constructed by invertibly mapping this set of symbols (through, say, an invertible function h) to the set of digits of a bijective base-K numeral system. A formula consisting of a string of n symbols
would then be mapped to the number
In other words, by placing the set of K basic symbols in some fixed order, such that the ith symbol corresponds uniquely to the ith digit of a bijective base-K numeral system, each formula may serve just as the very numeral of its own Gödel number.
of the theory can be expressed as a function on the natural numbers. If f is the Gödel mapping and if formula C can be derived from formulas A and B through an inference rule r; i.e.
then there should be some arithmetical function gr of natural numbers such that
This is true for the numbering Gödel used, and for any other numbering where the encoded formula can be arithmetically recovered from its Gödel number.
Thus, in a formal theory such as Peano arithmetic in which one can make statements about numbers and their arithmetical relationships to each other, one can use a Gödel numbering to indirectly make statements about the theory itself. This technique allowed Gödel to prove results about the consistency and completeness properties of formal system
s.
, the term "Gödel numbering" is used in settings more general than the one described above. It can refer to:
Also, the term Gödel numbering is sometimes used when the assigned "numbers" are actually strings, which is necessary when considering models of computation such as Turing machine
s that manipulate strings rather than numbers.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, a Gödel numbering is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
that assigns to each symbol and well-formed formula
Well-formed formula
In mathematical logic, a well-formed formula, shortly wff, often simply formula, is a word which is part of a formal language...
of some formal language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
a unique natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
, called its Gödel number. The concept was famously used by Kurt Gödel
Kurt Gödel
Kurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the...
for the proof of his incompleteness theorems
Gödel's incompleteness theorems
Gödel's incompleteness theorems are two theorems of mathematical logic that establish inherent limitations of all but the most trivial axiomatic systems capable of doing arithmetic. The theorems, proven by Kurt Gödel in 1931, are important both in mathematical logic and in the philosophy of...
.
A Gödel numbering can be interpreted as an encoding
Semantics encoding
A semantics encoding is a translation between formal languages. For programmers, the most familiar form of encoding is the compilation of a programming language into machine code or byte-code. Conversion between document formats are also forms of encoding. Compilation of TeX or LaTeX documents to...
in which a number is assigned to each symbol
Symbol
A symbol is something which represents an idea, a physical entity or a process but is distinct from it. The purpose of a symbol is to communicate meaning. For example, a red octagon may be a symbol for "STOP". On a map, a picture of a tent might represent a campsite. Numerals are symbols for...
of a mathematical notation
Mathematical notation
Mathematical notation is a system of symbolic representations of mathematical objects and ideas. Mathematical notations are used in mathematics, the physical sciences, engineering, and economics...
, after which a sequence of natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s can then represent a sequence of strings. These sequences of natural numbers can again be represented by single natural numbers, facilitating their manipulation in formal theories of arithmetic.
Since Gödel's paper was published in 1931, the term "Gödel numbering" or "Gödel code" has been used to refer to more general assignments of natural numbers to mathematical objects.
Simplified overview
Gödel noted that statements within a system can be represented by natural numbers. The significance of this was that properties of statements - such as their truth and falsehood - would be equivalent to determining whether their Gödel numbers had certain properties. The numbers involved might be very long indeed (in terms of number of digits), but this is not a barrier; all that matters is that we can show such numbers can be constructed.In simple terms, we devise a method by which every formula or statement that can be formulated in our system gets a unique number, in such a way that we can mechanically convert back and forth between formulas and Gödel numbers. Clearly there are many ways this can be done. Given any statement, the number it is converted to is known as its Gödel number. A simple example is the way in which English is stored as a sequence of numbers in computers using ASCII
ASCII
The American Standard Code for Information Interchange is a character-encoding scheme based on the ordering of the English alphabet. ASCII codes represent text in computers, communications equipment, and other devices that use text...
or Unicode
Unicode
Unicode is a computing industry standard for the consistent encoding, representation and handling of text expressed in most of the world's writing systems...
:
- The word HELLO is represented by 72-69-76-76-79 using decimal ASCIIASCIIThe American Standard Code for Information Interchange is a character-encoding scheme based on the ordering of the English alphabet. ASCII codes represent text in computers, communications equipment, and other devices that use text...
, ie the number 7269767679. - The logical statement x=y => y=x is represented by 120-061-121-032-061-062-032-121-061-120 using octal ASCIIASCIIThe American Standard Code for Information Interchange is a character-encoding scheme based on the ordering of the English alphabet. ASCII codes represent text in computers, communications equipment, and other devices that use text...
, ie the number 120061121032061062032121061120.
Gödel's encoding
Gödel used a system based on prime factorization. He first assigned a unique natural number to each basic symbol in the formal language of arithmetic with which he was dealing.To encode an entire formula, which is a sequence of symbols, Gödel used the following system. Given a sequence
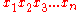of positive integers, the Gödel encoding of the sequence is the product of the first n primes raised to their corresponding values in the sequence: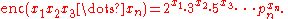According to the fundamental theorem of arithmetic
Fundamental theorem of arithmetic
In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
, any number obtained in this way can be uniquely factored into prime factor
Prime factor
In number theory, the prime factors of a positive integer are the prime numbers that divide that integer exactly, without leaving a remainder. The process of finding these numbers is called integer factorization, or prime factorization. A prime factor can be visualized by understanding Euclid's...
s, so it is possible to recover the original sequence from its Gödel number (for any given number n of symbols to be encoded).
Gödel specifically used this scheme at two levels: first, to encode sequences of symbols representing formulas, and second, to encode sequences of formulas representing proofs. This allowed him to show a correspondence between statements about natural numbers and statements about the provability of theorems about natural numbers, the key observation of the proof.
There are more sophisticated (and more concise) ways to construct a Gödel numbering for sequences
Gödel numbering for sequences
A Gödel numbering for sequences provides us an effective way to represent each finite sequence of natural numbers as a single natural number. Of course, the embedding is surely possible set theoretically, but the emphasis is on the effectiveness of the functions manipulating such representations of...
.
Example
In the specific Gödel numbering used by Nagel and Newman, the Gödel number for the symbol "0" is 6 and the Gödel number for the symbol "=" is 5. Thus, in their system, the Gödel number of the formula "0 = 0" is 26 × 35 × 56 = 243,000,000.Lack of uniqueness
A Gödel numbering is not unique, in that for any proof using Gödel numbers, there are infinitely many ways in which these numbers could be defined.For example, supposing there are K basic symbols, an alternative Gödel numbering could be constructed by invertibly mapping this set of symbols (through, say, an invertible function h) to the set of digits of a bijective base-K numeral system. A formula consisting of a string of n symbols
would then be mapped to the numberIn other words, by placing the set of K basic symbols in some fixed order, such that the ith symbol corresponds uniquely to the ith digit of a bijective base-K numeral system, each formula may serve just as the very numeral of its own Gödel number.
Application to formal arithmetic
Once a Gödel numbering for a formal theory is established, each inference ruleRule of inference
In logic, a rule of inference, inference rule, or transformation rule is the act of drawing a conclusion based on the form of premises interpreted as a function which takes premises, analyses their syntax, and returns a conclusion...
of the theory can be expressed as a function on the natural numbers. If f is the Gödel mapping and if formula C can be derived from formulas A and B through an inference rule r; i.e.
then there should be some arithmetical function gr of natural numbers such that
This is true for the numbering Gödel used, and for any other numbering where the encoded formula can be arithmetically recovered from its Gödel number.
Thus, in a formal theory such as Peano arithmetic in which one can make statements about numbers and their arithmetical relationships to each other, one can use a Gödel numbering to indirectly make statements about the theory itself. This technique allowed Gödel to prove results about the consistency and completeness properties of formal system
Formal system
In formal logic, a formal system consists of a formal language and a set of inference rules, used to derive an expression from one or more other premises that are antecedently supposed or derived . The axioms and rules may be called a deductive apparatus...
s.
Generalizations
In computability theoryComputability theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
, the term "Gödel numbering" is used in settings more general than the one described above. It can refer to:
- Any assignment of the elements of a formal languageFormal languageA formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
to natural numbers in such a way that the numbers can be manipulated by an algorithmAlgorithmIn mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
to simulate manipulation of elements of the formal language. - More generally, an assignment of elements from a countable mathematical object, such as a countable groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, to natural numbers to allow algorithmic manipulation of the mathematical object.
Also, the term Gödel numbering is sometimes used when the assigned "numbers" are actually strings, which is necessary when considering models of computation such as Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
s that manipulate strings rather than numbers.
Gödel sets
Gödel sets are sometimes used in set theory to encode formulas, and are similar to Gödel numbers, except that one uses sets rather than numbers to do the encoding. In simple cases when one uses hereditarily finite set to encode formulas this is essentially equivalent to the use of Gödel numbers, but somewhat easier to define because the tree structure of formulas can be modeled by the tree structure of sets. Gödel sets can also be used to encode formulas in infinitary languages.See also
- Church numeral
- Description numberDescription numberDescription numbers are numbers that arise in the theory of Turing machines. They are very similar to Gödel numbers, and are also occasionally called "Gödel numbers" in the literature. Given some universal Turing machine, every Turing machine can, given its encoding on that machine, be assigned a...
- Gödel's incompleteness theoremsGödel's incompleteness theoremsGödel's incompleteness theorems are two theorems of mathematical logic that establish inherent limitations of all but the most trivial axiomatic systems capable of doing arithmetic. The theorems, proven by Kurt Gödel in 1931, are important both in mathematical logic and in the philosophy of...
- Chaitin's incompleteness theorem
Further reading
- Gödel, Escher, Bach: an Eternal Golden BraidGödel, Escher, BachGödel, Escher, Bach: An Eternal Golden Braid is a book by Douglas Hofstadter, described by his publishing company as "a metaphorical fugue on minds and machines in the spirit of Lewis Carroll"....
, by Douglas HofstadterDouglas HofstadterDouglas Richard Hofstadter is an American academic whose research focuses on consciousness, analogy-making, artistic creation, literary translation, and discovery in mathematics and physics...
. This book defines and uses an alternative Gödel numbering. - I Am a Strange LoopI Am a Strange LoopI Am a Strange Loop is a 2007 book by Douglas Hofstadter, examining in depth the concept of a strange loop originally developed in his 1979 book Gödel, Escher, Bach....
by Douglas HofstadterDouglas HofstadterDouglas Richard Hofstadter is an American academic whose research focuses on consciousness, analogy-making, artistic creation, literary translation, and discovery in mathematics and physics...
. This is a newer book by Hofstadter that includes the history of Gödel's numbering.