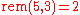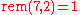Gödel numbering for sequences
Encyclopedia
A Gödel numbering for sequences provides us an effective way to represent each finite sequence of natural numbers as a single natural number. Of course, the embedding
is surely possible set theoretically, but the emphasis is on the effectiveness of the functions manipulating such representations of sequences: the operations on sequences (accessing individual members, concatenation) can be "implemented" using total recursive functions.
It is usually used to build sequential “data type
s” in the realm of arithmetic-based formalizations of some fundamental notions of mathematics. It is a specific case of the more general idea of Gödel numbering.
E.g. recursive function theory
can be regarded as a formalization of notion “algorithm
”, and if we regard it as a programming language
, we can mimic arrays, lists by encoding a sequence of natural numbers in a single natural number — to achieve this, we can use various number theoretic
ideas. Using the fundamental theorem of arithmetic
is a straightforward way, but there are also more ergonomic approaches, e.g. using pairing function
combined with Chinese remainder theorem
in a sophisticated way.
or one-to-one correspondence with the sequences) but also to encode whole “architectures” of sophisticated “machines”. For example we can encode Markov algorithm
s, or Turing machine
s into natural numbers and thereby prove that the expressing power of recursive function theory is no less than that of the former machine-like formalizations of algorithms.
.
Anyway, we expect that this obtaining back information can be done in an effective way, by an appropriate total recursive function.
We want a totally recursive function f that satisfies:
For all n and for any n-length sequence of natural numbers
, there exists an appropriate natural number a, called the Gödel number of the sequence such that for all i in the range of 0 … n-1
There exist effective functions enabling us to obtain back each member of the original sequence from a Gödel number of the sequence. Moreover, there are ways to define some in a constructive
way, thus we are not forced to be satisfied with mere proofs of existence.
, we can define constructively such a recursive function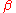
(using simple number-theoretical functions, all of which can be defined in a total recursive way) fulfilling the "specifications" given above. Also Gödel defined the 
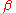function using the Chinese remainder theorem in his article written in 1931. This is a primitive recursive function
.
Thus, for all n and for any n-length sequence of natural numbers
, there exists an appropriate natural number a, called the Gödel number of the sequence such that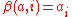
from the details of the “implementation
” of the pairing function, we need only to know its “interface
”: let
, K, L denote the pairing function and its two projection
functions, respectively, satisying specification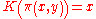
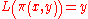
we shall not discuss and formalize the axiom for excluding alien objects here, it is now not so important.
It can be proven that this function can be "implemented" as a recursive function.
Using the Chinese remainder theorem
, we can prove that implementing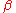
as
will work, according to the specification we expect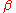
to satisfy. We can use a more concise form by an abuse of notation
(sort of pattern matching
):
Let us achieve even more readability by more modularity
and reuse
(as these notions are used in computer science): defining
the sequence 
,
enables us to write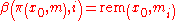
We shall use this
notation also in the proof.
For proving the correctness of the above definition of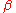
function, we shall use (and prove) several auxiliary theorems, lemmas. These have their own assumptions. Now we try to find out these assumptions, calibrating and tuning their strength carefully: they should not be said in an either superfluously sharp, or unsatisfactorily weak form.
Let
be a sequence of natural numbers.
Let m be chosen to satisfy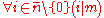
The first assumption is meant as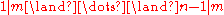
It is needed to achieve that the assumption of the Chinese remainder theorem (that of being pairwise coprime
) can be met. In the literature, sometimes this requirement is replaced with a stronger one, e.g. constructively
built with the factorial
function, but the proof uses just that many strength as formulated here.
The second assumption does not concern the Chinese remainder theorem in any way. It will have importance in proving that the specification for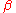
is met eventually. It ensures that an 
solution of the simultaneous congruence system
for each i ranging 0,… , n-1
also satisfies
A stronger assumption for m requiring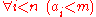
automatically satisfies it (if we define the notation 
as above).
As mentioned in section Hand-tuned assumptions, we prescribed that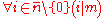
thus we can use it.
What we want to prove is that we can produce a sequence of pairwise coprime
numbers in a way that will turn out to correspond to the Implementation of the β function in a sense.
In details: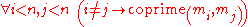
let us remember,
we defined 
.
Let us use reductio ad absurdum
!
Negation of the original statement:
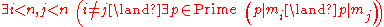
Using a “more” prenex normal form
(but note allowing a constraint-like notation in quantifiers):
Because of a theorem on divisibility
,
allows us to say also
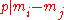
Substituting the definens
of
-sequence notation, we get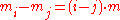 
, thus (as equality axioms postulate identity to be a congruence relation
) we get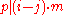
Using that p is a prime element
(note: not the irreducible element
property is used!), we get
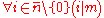
let us remember, we have planned this assumption calibrated carefully to be as weak as possible, but strong enough to enable us to use it now.
The assumed negation of the original statement (let us remember, we use reductio ad absurdum) contains an appropriate existential statement using indices
, this entails 
, thus the mentioned assumption can be applied, so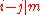 
holds.
, that
holds.
Because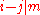
entails (by the transitivity
property of the divisibility
relation) that
, thus (as equality axioms postulate identiy to be a congruence relation )
can be proven.
and we have just proved
thus also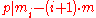
should hold.
But, after substituting the definiens
for
, we shall see
Thus, summarizing the above three statements, by transitivity
of the equality, also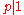
should hold. But let us look up the quantification of p in the negation of the original statement: p is existentially quantified and restricted to primes
The above statement together with the above quantification of p establish the contradiction we wanted to reach.
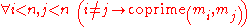
We can write it in a more concise way: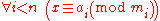
In the followings, many statements will be said, all beginning with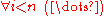
. To achieve a more ergonomic treatment, from now on all statements will be regarded in the scope of an 
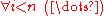qantification. Thus: 
begins!
Let us chose a solution
for the system of simultaneous congruences. At least one solution must exist, because 
are pairwise comprime (that's what we have been proving so long in the previous sections!), thus we can refer to the Chinese remainder theorem's ensuring solution. Thus, from now on, we can regard 
satisfying
it means (by definition of modular arithmetic
) that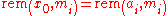
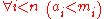”. Let us remember: we are now in the scope of a “big” quantification for i, thus we don't repeat its quantification for each statement.
The second hand-tuned assumption
will join in at this point, because it entails that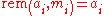
Now by transitivity
of equality we get
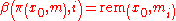
is good for achieving what we declared in the specification of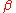
: we want 
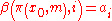to hold.
That's it, it can be seen now by transitivity
of equality, looking at the above three equations.
Scope of i ends here.
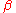: its specification requiring
is met. Although proving this was the most important, if we want to establish an encoding scheme for sequences, but we have to fill in some gaps yet. These are related notions similar to existence
and uniqueness
(although on uniqueness, “at most one” should be meant here, and the conjunction of both is delayed as a final result).
? The specification declares only an existential quantification, not yet a functional connection. We want a constructive
and algorithmic way, even more, a (total) recursive function for the encoding.
, and the totality of the resulting function is ensured by everything we have proven till now (i.e. the correctness of the definition of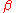
by meeting its specification). In fact, the specification
plays a role here of a more general notion (“special function”). The importance of this notion is that it enables us to split off the (sub)class of (total) recursive functions from the (super)class of partial recursive functions. In brief, the specification says exactly: a function f
satisfying specification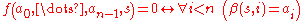
is a special function, i.e. for each fixed combination of all-but-last arguments, the function f has root in its last argument: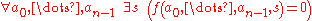
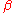function :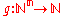
and it can be proven (using the notions of the previous section ) that g is (total) recursive.
way as arrays are used in programming.
But sometimes we need dynamically stretching sequences, or we need to deal with sequences whose length cannot be type
d in a static way. In other words, we may encode sequences in an analogous way as we use lists in programming.
An example for both cases: if we make the Gödel numbering of a Turing machine, then the each row in matrix of the “program” can be represented with tuples, sequences of fixed length (thus, without storing the length), because the number of the columns is fixed. But if we want to reason about configuration-like things (of Turing-machines), and specially, we want to encode the significant part of the tape of a running Turing machine, then we have to represent sequences together with their length. Moreover, we can mimic dynamically stretching sequences by representing sequence concatenation (or at least, augmenting a sequence with one more element) with a [totally] recursive function.
Length can be stored stored simply as a surplus member:
The corresponding modification of the proof is straightforward, by adding a surplus
to the system of simultaneous congruences (provided that the surplus member index is chosen to be 0). Also the assumptions etc. have to be modified accordingly.
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
is surely possible set theoretically, but the emphasis is on the effectiveness of the functions manipulating such representations of sequences: the operations on sequences (accessing individual members, concatenation) can be "implemented" using total recursive functions.
It is usually used to build sequential “data type
Data type
In computer programming, a data type is a classification identifying one of various types of data, such as floating-point, integer, or Boolean, that determines the possible values for that type; the operations that can be done on values of that type; the meaning of the data; and the way values of...
s” in the realm of arithmetic-based formalizations of some fundamental notions of mathematics. It is a specific case of the more general idea of Gödel numbering.
E.g. recursive function theory
Mu-recursive function
In mathematical logic and computer science, the μ-recursive functions are a class of partial functions from natural numbers to natural numbers which are "computable" in an intuitive sense. In fact, in computability theory it is shown that the μ-recursive functions are precisely the functions that...
can be regarded as a formalization of notion “algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
”, and if we regard it as a programming language
Programming language
A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
, we can mimic arrays, lists by encoding a sequence of natural numbers in a single natural number — to achieve this, we can use various number theoretic
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
ideas. Using the fundamental theorem of arithmetic
Fundamental theorem of arithmetic
In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
is a straightforward way, but there are also more ergonomic approaches, e.g. using pairing function
Pairing function
In mathematics a pairing function is a process to uniquely encode two natural numbers into a single natural number.Any pairing function can be used in set theory to prove that integers and rational numbers have the same cardinality as natural numbers...
combined with Chinese remainder theorem
Chinese remainder theorem
The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
in a sophisticated way.
Gödel numbering
Gödel numbering is a sweeping idea that can be used to not only encode unique sequences of symbols into unique natural numbers (i.e. place numbers into mutually exclusiveMutually exclusive
In layman's terms, two events are mutually exclusive if they cannot occur at the same time. An example is tossing a coin once, which can result in either heads or tails, but not both....
or one-to-one correspondence with the sequences) but also to encode whole “architectures” of sophisticated “machines”. For example we can encode Markov algorithm
Markov algorithm
In theoretical computer science, a Markov algorithm is a string rewriting system that uses grammar-like rules to operate on strings of symbols. Markov algorithms have been shown to be Turing-complete, which means that they are suitable as a general model of computation and can represent any...
s, or Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
s into natural numbers and thereby prove that the expressing power of recursive function theory is no less than that of the former machine-like formalizations of algorithms.
Accessing members
We expect from any such representation of sequences that we can get back all the information from it that is contained by the original sequence: most important, to access each individual member. We are not sticked necessarily to require that also the length can be obtained directly: even if we want to handle sequences of different length, we can store length data as a surplus member, or as the other member of an ordered pair by using a pairing functionPairing function
In mathematics a pairing function is a process to uniquely encode two natural numbers into a single natural number.Any pairing function can be used in set theory to prove that integers and rational numbers have the same cardinality as natural numbers...
.
Anyway, we expect that this obtaining back information can be done in an effective way, by an appropriate total recursive function.
We want a totally recursive function f that satisfies:
For all n and for any n-length sequence of natural numbers
, there exists an appropriate natural number a, called the Gödel number of the sequence such that for all i in the range of 0 … n-1There exist effective functions enabling us to obtain back each member of the original sequence from a Gödel number of the sequence. Moreover, there are ways to define some in a constructive
Constructive proof
In mathematics, a constructive proof is a method of proof that demonstrates the existence of a mathematical object with certain properties by creating or providing a method for creating such an object...
way, thus we are not forced to be satisfied with mere proofs of existence.
Gödel's β-function lemma
By an ingenious use of Chinese remainder theoremChinese remainder theorem
The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
, we can define constructively such a recursive function
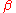(using simple number-theoretical functions, all of which can be defined in a total recursive way) fulfilling the "specifications" given above. Also Gödel defined the 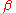function using the Chinese remainder theorem in his article written in 1931. This is a primitive recursive functionPrimitive recursive function
The primitive recursive functions are defined using primitive recursion and composition as central operations and are a strict subset of the total µ-recursive functions...
.
Thus, for all n and for any n-length sequence of natural numbers
, there exists an appropriate natural number a, called the Gödel number of the sequence such that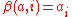Using a pairing function
Our specific solution will depend on a pairing function — there are several ways to implement the latter, let us select one. Now, we can abstractAbstraction
Abstraction is a process by which higher concepts are derived from the usage and classification of literal concepts, first principles, or other methods....
from the details of the “implementation
Implementation
Implementation is the realization of an application, or execution of a plan, idea, model, design, specification, standard, algorithm, or policy.-Computer Science:...
” of the pairing function, we need only to know its “interface
Interface (computer science)
In the field of computer science, an interface is a tool and concept that refers to a point of interaction between components, and is applicable at the level of both hardware and software...
”: let
, K, L denote the pairing function and its two projectionProjection (mathematics)
Generally speaking, in mathematics, a projection is a mapping of a set which is idempotent, which means that a projection is equal to its composition with itself. A projection may also refer to a mapping which has a left inverse. Bot notions are strongly related, as follows...
functions, respectively, satisying specification
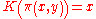
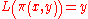
we shall not discuss and formalize the axiom for excluding alien objects here, it is now not so important.
Remainder for natural numbers
We shall use another auxiliary function: it will compute the remainder for natural numbers. Examples:
It can be proven that this function can be "implemented" as a recursive function.
Implementation of the β function
Using the Chinese remainder theorem
Chinese remainder theorem
The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
, we can prove that implementing
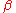aswill work, according to the specification we expect
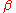to satisfy. We can use a more concise form by an abuse of notationAbuse of notation
In mathematics, abuse of notation occurs when an author uses a mathematical notation in a way that is not formally correct but that seems likely to simplify the exposition or suggest the correct intuition . Abuse of notation should be contrasted with misuse of notation, which should be avoided...
(sort of pattern matching
Pattern matching
In computer science, pattern matching is the act of checking some sequence of tokens for the presence of the constituents of some pattern. In contrast to pattern recognition, the match usually has to be exact. The patterns generally have the form of either sequences or tree structures...
):
Let us achieve even more readability by more modularity
Modularity (programming)
Modular programming is a software design technique that increases the extent to which software is composed of separate, interchangeable components called modules by breaking down program functions into modules, each of which accomplishes one function and contains everything necessary to accomplish...
and reuse
Code reuse
Code reuse, also called software reuse, is the use of existing software, or software knowledge, to build new software.-Overview:Ad hoc code reuse has been practiced from the earliest days of programming. Programmers have always reused sections of code, templates, functions, and procedures...
(as these notions are used in computer science): defining
the sequence ,enables us to write
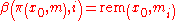
We shall use this
notation also in the proof.Hand-tuned assumptions
For proving the correctness of the above definition of
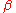function, we shall use (and prove) several auxiliary theorems, lemmas. These have their own assumptions. Now we try to find out these assumptions, calibrating and tuning their strength carefully: they should not be said in an either superfluously sharp, or unsatisfactorily weak form.Let
be a sequence of natural numbers.Let m be chosen to satisfy
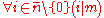
The first assumption is meant as
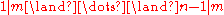
It is needed to achieve that the assumption of the Chinese remainder theorem (that of being pairwise coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
) can be met. In the literature, sometimes this requirement is replaced with a stronger one, e.g. constructively
Constructive proof
In mathematics, a constructive proof is a method of proof that demonstrates the existence of a mathematical object with certain properties by creating or providing a method for creating such an object...
built with the factorial
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
function, but the proof uses just that many strength as formulated here.
The second assumption does not concern the Chinese remainder theorem in any way. It will have importance in proving that the specification for
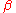is met eventually. It ensures that an solution of the simultaneous congruence system for each i ranging 0,… , n-1also satisfies
A stronger assumption for m requiring
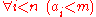automatically satisfies it (if we define the notation as above).Proof that (coprimality) assumption for Chinese remainder theorem is met
We shall prove that the (coprimality) assumption for Chinese remainder theorem is met.As mentioned in section Hand-tuned assumptions, we prescribed that
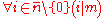
thus we can use it.
What we want to prove is that we can produce a sequence of pairwise coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
numbers in a way that will turn out to correspond to the Implementation of the β function in a sense.
In details:
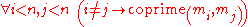
let us remember,
we defined .Let us use reductio ad absurdum
Reductio ad absurdum
In logic, proof by contradiction is a form of proof that establishes the truth or validity of a proposition by showing that the proposition's being false would imply a contradiction...
!
Negation of the original statement:
First steps
We know what “coprime” relation means (in a lucky way, its negation can be formulated in a concise form), thus, let us substitute in the appropriate way: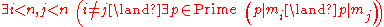Using a “more” prenex normal form
Prenex normal form
A formula of the predicate calculus is in prenex normal form if it is written as a string of quantifiers followed by a quantifier-free part .Every formula in classical logic is equivalent to a formula in prenex normal form...
(but note allowing a constraint-like notation in quantifiers):
Because of a theorem on divisibility
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
,
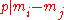
allows us to say alsoSubstituting the definens
Definition
A definition is a passage that explains the meaning of a term , or a type of thing. The term to be defined is the definiendum. A term may have many different senses or meanings...
of
-sequence notation, we get 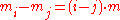, thus (as equality axioms postulate identity to be a congruence relationCongruence relation
In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
) we get
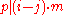
Using that p is a prime element
Prime element
In abstract algebra, an element p of a commutative ring R is said to be prime if it is not zero, not a unit and whenever p divides ab for some a and b in R, then p divides a or p divides b...
(note: not the irreducible element
Irreducible element
In abstract algebra, a non-zero non-unit element in an integral domain is said to be irreducible if it is not a product of two non-units.Irreducible elements should not be confused with prime elements...
property is used!), we get
Resorting to the first hand-tuned assumption
Now this is the point in the proof where we must resort to our assumption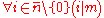let us remember, we have planned this assumption calibrated carefully to be as weak as possible, but strong enough to enable us to use it now.
The assumed negation of the original statement (let us remember, we use reductio ad absurdum) contains an appropriate existential statement using indices
, this entails , thus the mentioned assumption can be applied, so 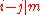holds.Using an (object) theorem of the propositional calculus as a lemma
We can prove by several means known in propositional calculusPropositional calculus
In mathematical logic, a propositional calculus or logic is a formal system in which formulas of a formal language may be interpreted as representing propositions. A system of inference rules and axioms allows certain formulas to be derived, called theorems; which may be interpreted as true...
, that
holds.
Because
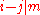entails (by the transitivityTransitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
property of the divisibility
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
relation) that
, thus (as equality axioms postulate identiy to be a congruence relation )can be proven.
Reaching the contradiction
The negation of original statement containedand we have just proved
thus also
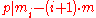
should hold.
But, after substituting the definiens
Definition
A definition is a passage that explains the meaning of a term , or a type of thing. The term to be defined is the definiendum. A term may have many different senses or meanings...
for
, we shall seeThus, summarizing the above three statements, by transitivity
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
of the equality, also
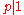
should hold. But let us look up the quantification of p in the negation of the original statement: p is existentially quantified and restricted to primes
The above statement together with the above quantification of p establish the contradiction we wanted to reach.
End of reductio ad absurdum
By reaching contradiction with its negation, we have just proven the original statement: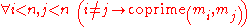The system of simultaneous congruences
We build a system of simultaneous congruences
We can write it in a more concise way:
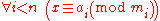
In the followings, many statements will be said, all beginning with
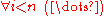. To achieve a more ergonomic treatment, from now on all statements will be regarded in the scope of an 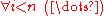qantification. Thus: begins!Let us chose a solution
for the system of simultaneous congruences. At least one solution must exist, because are pairwise comprime (that's what we have been proving so long in the previous sections!), thus we can refer to the Chinese remainder theorem's ensuring solution. Thus, from now on, we can regard satisfyingit means (by definition of modular arithmetic
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
) that
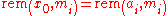
Resorting to the second hand-tuned assumption
Again, we must resort to the assumptions whose strength we specifically “tuned” for using in the proof. But now, it is the second assumption (which does not concern the Chinese remainder theorem in any way) that we need: “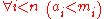”. Let us remember: we are now in the scope of a “big” quantification for i, thus we don't repeat its quantification for each statement.The second hand-tuned assumption
will join in at this point, because it entails that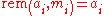Now by transitivity
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
of equality we get
QED
Our original goal was to prove that the definition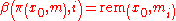is good for achieving what we declared in the specification of
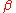: we want 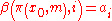to hold.That's it, it can be seen now by transitivity
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
of equality, looking at the above three equations.
Scope of i ends here.
Existence and uniqueness
We have just proven the correctness of the definition of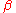: its specification requiringis met. Although proving this was the most important, if we want to establish an encoding scheme for sequences, but we have to fill in some gaps yet. These are related notions similar to existence
Existential quantification
In predicate logic, an existential quantification is the predication of a property or relation to at least one member of the domain. It is denoted by the logical operator symbol ∃ , which is called the existential quantifier...
and uniqueness
Uniqueness quantification
In mathematics and logic, the phrase "there is one and only one" is used to indicate that exactly one object with a certain property exists. In mathematical logic, this sort of quantification is known as uniqueness quantification or unique existential quantification.Uniqueness quantification is...
(although on uniqueness, “at most one” should be meant here, and the conjunction of both is delayed as a final result).
Uniqueness of encoding, achieved by minimalization
Because let us remember, our ultimate question is: what number should stand for the encoding of sequence? The specification declares only an existential quantification, not yet a functional connection. We want a constructiveConstructive proof
In mathematics, a constructive proof is a method of proof that demonstrates the existence of a mathematical object with certain properties by creating or providing a method for creating such an object...
and algorithmic way, even more, a (total) recursive function for the encoding.
Totality, because minimalization is restricted to special functions
This gap can be filled in in a straightforward way: we shall use minimalizationMu operator
In computability theory, the μ operator, minimization operator, or unbounded search operator searches for the least natural number with a given property.- Definition :...
, and the totality of the resulting function is ensured by everything we have proven till now (i.e. the correctness of the definition of
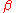by meeting its specification). In fact, the specificationplays a role here of a more general notion (“special function”). The importance of this notion is that it enables us to split off the (sub)class of (total) recursive functions from the (super)class of partial recursive functions. In brief, the specification says exactly: a function f
satisfying specification
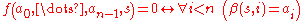
is a special function, i.e. for each fixed combination of all-but-last arguments, the function f has root in its last argument:
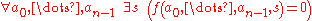
The Gödel numbering function g can be chosen to be total recursive
Thus, let us choose the minimal possible number that fits well in the specification of the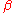 function :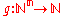and it can be proven (using the notions of the previous section ) that g is (total) recursive.
Access of length
If we use the above scheme for encoding sequences only in contexts where the length of the sequences is fixed, then no problem arises. In other words, we can use them in an analogousAnalogy
Analogy is a cognitive process of transferring information or meaning from a particular subject to another particular subject , and a linguistic expression corresponding to such a process...
way as arrays are used in programming.
But sometimes we need dynamically stretching sequences, or we need to deal with sequences whose length cannot be type
Typeful programming
In computer science, typeful programming is a programming style identified by widespread use of type information handled through mechanical typechecking techniques. The concept was introduced in a paper of the same name by Luca Cardelli in 1991....
d in a static way. In other words, we may encode sequences in an analogous way as we use lists in programming.
An example for both cases: if we make the Gödel numbering of a Turing machine, then the each row in matrix of the “program” can be represented with tuples, sequences of fixed length (thus, without storing the length), because the number of the columns is fixed. But if we want to reason about configuration-like things (of Turing-machines), and specially, we want to encode the significant part of the tape of a running Turing machine, then we have to represent sequences together with their length. Moreover, we can mimic dynamically stretching sequences by representing sequence concatenation (or at least, augmenting a sequence with one more element) with a [totally] recursive function.
Length can be stored stored simply as a surplus member:
The corresponding modification of the proof is straightforward, by adding a surplus
to the system of simultaneous congruences (provided that the surplus member index is chosen to be 0). Also the assumptions etc. have to be modified accordingly.