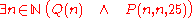Existential quantification
Encyclopedia
In predicate logic
, an existential quantification is the predication of a property or relation to at least one member of the domain. It is denoted by the logical operator symbol ∃ , which is called the existential quantifier. Existential quantification is distinct from universal quantification
("for all"), which asserts that the property or relation holds for any members of the domain.
Symbols are encoded and .
multiplied by itself is 25.
This would seem to be a logical disjunction
because of the repeated use of "or". However, the "and so on" makes this impossible to integrate and to interpret as a disjunction in formal logic
.
Instead, the statement could be rephrased more formally as
This is a single statement using existential quantification.
This statement is more precise than the original one, as the phrase "and so on" does not necessarily include all natural number
s, and nothing more. Since the domain was not stated explicitly, the phrase could not be interpreted formally. In the quantified statement, on the other hand, the natural numbers are mentioned explicitly.
This particular example is true, because 5 is a natural number, and when we substitute 5 for n, we produce "5·5 = 25", which is true.
It does not matter that "n·n = 25" is only true for a single natural number, 5; even the existence of a single solution
is enough to prove the existential quantification true.
In contrast, "For some even number n, n·n = 25" is false, because there are no even solutions.
The domain of discourse
, which specifies which values the variable n is allowed to take, is therefore of critical importance in a statement's trueness or falseness. Logical conjunction
s are used to restrict the domain of discourse to fulfill a given predicate. For example:
is logically equivalent to
Here, "and" is the logical conjunction.
In symbolic logic
, "∃" (a backwards letter "E
" in a sans-serif
font) is used to indicate existential quantification. Thus, if P(a, b, c) is the predicate "a·b = c" and
is the set of natural numbers, then
is the (true) statement
Similarly, if Q(n) is the predicate "n is even", then
is the (false) statement
In mathematics
, the proof of a "some" statement may be achieved either by a constructive proof
, which exhibits an object satisfying the "some" statement, or by a nonconstructive proof which shows that there must be such an object but without exhibiting one.
symbol is used to denote negation.
For example, if P(x) is the propositional function "x is between 0 and 1", then, for a domain of discourse X of all natural numbers, the existential quantification "There exists a natural number x which is between 0 and 1" is symbolically stated: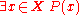
This can be demonstrated to be irrevocably false. Truthfully, it must be said, "It is not the case that there is a natural number x that is between 0 and 1", or, symbolically: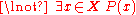
.
If there is no element of the domain of discourse for which the statement is true, then it must be false for all of those elements. That is, the negation of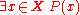
is logically equivalent to "For any natural number x, x is not between 0 and 1", or: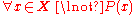
Generally, then, the negation of a propositional function
's existential quantification is a universal quantification
of that propositional function's negation; symbolically,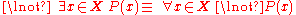
A common error is stating "all persons are not married" (i.e. "there exists no person who is married") when "not all persons are married" (i.e. "there exists a person who is not married") is intended:
Negation is also expressible through a statement of "for no", as opposed to "for some":
Unlike the universal quantifier, the existential quantifier distributes over logical disjunctions:
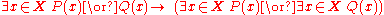
is a rule justifying a logical step from hypothesis to conclusion. There are several rules of inference which utilize the existential quantifier.
Existential introduction (∃I) concludes that, if the propositional function is known to be true for a particular element of the domain of discourse, then it must be true that there exists an element for which the proposition function is true. Symbolically,
The reasoning behind existential elimination (∃E) is as follows: If it is given that there exists an element for which the proposition function is true, and if a conclusion can be reached by giving that element an arbitrary name, that conclusion is necessarily true, as long as it does not contain the name. Symbolically, for an arbitrary c and for a proposition Q in which c does not appear:
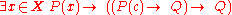
must be true for all values of c over the same domain X; else, the logic does not follow: If c is not arbitrary, and is instead a specific element of the domain of discourse, then stating P(c) might unjustifiably give more information about that object.
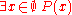is always false, regardless of P(x). This is because 
denotes the empty set
, and no x of any description – let alone an x fulfilling a given predicate P(x) – exist in the empty set. See also vacuous truth
.
Predicate logic
In mathematical logic, predicate logic is the generic term for symbolic formal systems like first-order logic, second-order logic, many-sorted logic or infinitary logic. This formal system is distinguished from other systems in that its formulae contain variables which can be quantified...
, an existential quantification is the predication of a property or relation to at least one member of the domain. It is denoted by the logical operator symbol ∃ , which is called the existential quantifier. Existential quantification is distinct from universal quantification
Universal quantification
In predicate logic, universal quantification formalizes the notion that something is true for everything, or every relevant thing....
("for all"), which asserts that the property or relation holds for any members of the domain.
Symbols are encoded and .
Basics
Consider a formula that states that some natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
multiplied by itself is 25.
-
0·0 = 25, or 1·1 = 25, or 2·2 = 25, or 3·3 = 25, and so on.
This would seem to be a logical disjunction
Logical disjunction
In logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...
because of the repeated use of "or". However, the "and so on" makes this impossible to integrate and to interpret as a disjunction in formal logic
Formal logic
Classical or traditional system of determining the validity or invalidity of a conclusion deduced from two or more statements...
.
Instead, the statement could be rephrased more formally as
For some natural number n, n·n = 25.
This is a single statement using existential quantification.
This statement is more precise than the original one, as the phrase "and so on" does not necessarily include all natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s, and nothing more. Since the domain was not stated explicitly, the phrase could not be interpreted formally. In the quantified statement, on the other hand, the natural numbers are mentioned explicitly.
This particular example is true, because 5 is a natural number, and when we substitute 5 for n, we produce "5·5 = 25", which is true.
It does not matter that "n·n = 25" is only true for a single natural number, 5; even the existence of a single solution
Solution
In chemistry, a solution is a homogeneous mixture composed of only one phase. In such a mixture, a solute is dissolved in another substance, known as a solvent. The solvent does the dissolving.- Types of solutions :...
is enough to prove the existential quantification true.
In contrast, "For some even number n, n·n = 25" is false, because there are no even solutions.
The domain of discourse
Domain of discourse
In the formal sciences, the domain of discourse, also called the universe of discourse , is the set of entities over which certain variables of interest in some formal treatment may range...
, which specifies which values the variable n is allowed to take, is therefore of critical importance in a statement's trueness or falseness. Logical conjunction
Logical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
s are used to restrict the domain of discourse to fulfill a given predicate. For example:
For some positive odd number n, n·n = 25"
is logically equivalent to
For some natural number n, n is odd and n·n = 25".
Here, "and" is the logical conjunction.
In symbolic logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
, "∃" (a backwards letter "E
E
E is the fifth letter and a vowel in the basic modern Latin alphabet. It is the most commonly used letter in the Czech, Danish, Dutch, English, French, German, Hungarian, Latin, Norwegian, Spanish, and Swedish languages.-History:...
" in a sans-serif
Sans-serif
In typography, a sans-serif, sans serif or san serif typeface is one that does not have the small projecting features called "serifs" at the end of strokes. The term comes from the French word sans, meaning "without"....
font) is used to indicate existential quantification. Thus, if P(a, b, c) is the predicate "a·b = c" and
is the set of natural numbers, then
is the (true) statement
-
For some natural number n, n·n = 25.
Similarly, if Q(n) is the predicate "n is even", then
is the (false) statement
-
For some even number n, n·n = 25.
In mathematics
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
, the proof of a "some" statement may be achieved either by a constructive proof
Constructive proof
In mathematics, a constructive proof is a method of proof that demonstrates the existence of a mathematical object with certain properties by creating or providing a method for creating such an object...
, which exhibits an object satisfying the "some" statement, or by a nonconstructive proof which shows that there must be such an object but without exhibiting one.
Negation
A quantified propositional function is a statement; thus, like statements, quantified functions can be negated. The symbol is used to denote negation.For example, if P(x) is the propositional function "x is between 0 and 1", then, for a domain of discourse X of all natural numbers, the existential quantification "There exists a natural number x which is between 0 and 1" is symbolically stated:
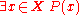
This can be demonstrated to be irrevocably false. Truthfully, it must be said, "It is not the case that there is a natural number x that is between 0 and 1", or, symbolically:
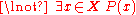.If there is no element of the domain of discourse for which the statement is true, then it must be false for all of those elements. That is, the negation of
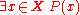
is logically equivalent to "For any natural number x, x is not between 0 and 1", or:
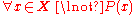
Generally, then, the negation of a propositional function
Propositional function
A propositional function in logic, is a statement expressed in a way that would assume the value of true or false, except that within the statement is a variable that is not defined or specified, which leaves the statement undetermined...
's existential quantification is a universal quantification
Universal quantification
In predicate logic, universal quantification formalizes the notion that something is true for everything, or every relevant thing....
of that propositional function's negation; symbolically,
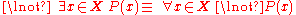
A common error is stating "all persons are not married" (i.e. "there exists no person who is married") when "not all persons are married" (i.e. "there exists a person who is not married") is intended:
Negation is also expressible through a statement of "for no", as opposed to "for some":
Unlike the universal quantifier, the existential quantifier distributes over logical disjunctions:
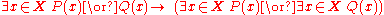
Rules of Inference
A rule of inferenceRule of inference
In logic, a rule of inference, inference rule, or transformation rule is the act of drawing a conclusion based on the form of premises interpreted as a function which takes premises, analyses their syntax, and returns a conclusion...
is a rule justifying a logical step from hypothesis to conclusion. There are several rules of inference which utilize the existential quantifier.
Existential introduction (∃I) concludes that, if the propositional function is known to be true for a particular element of the domain of discourse, then it must be true that there exists an element for which the proposition function is true. Symbolically,
The reasoning behind existential elimination (∃E) is as follows: If it is given that there exists an element for which the proposition function is true, and if a conclusion can be reached by giving that element an arbitrary name, that conclusion is necessarily true, as long as it does not contain the name. Symbolically, for an arbitrary c and for a proposition Q in which c does not appear:
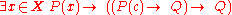
must be true for all values of c over the same domain X; else, the logic does not follow: If c is not arbitrary, and is instead a specific element of the domain of discourse, then stating P(c) might unjustifiably give more information about that object.The empty set
By convention, the formula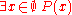 is always false, regardless of P(x). This is because denotes the empty setEmpty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
, and no x of any description – let alone an x fulfilling a given predicate P(x) – exist in the empty set. See also vacuous truth
Vacuous truth
A vacuous truth is a truth that is devoid of content because it asserts something about all members of a class that is empty or because it says "If A then B" when in fact A is inherently false. For example, the statement "all cell phones in the room are turned off" may be true...
.