
Logical conjunction
Encyclopedia
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
and mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false.
The analogue of conjunction for a (possibly infinite) family of statements is universal quantification
Universal quantification
In predicate logic, universal quantification formalizes the notion that something is true for everything, or every relevant thing....
, which is part of predicate logic
Predicate logic
In mathematical logic, predicate logic is the generic term for symbolic formal systems like first-order logic, second-order logic, many-sorted logic or infinitary logic. This formal system is distinguished from other systems in that its formulae contain variables which can be quantified...
.
Notation
And is usually expressed with the prefix operator K, or an infix operator. In mathematics and logic, the infix operator is usually ∧; in electronics ; and in programming languages, & or and. Some programming languages have a related control structure, the short-circuit and, written &&, and then, etc.
; and in programming languages, & or and. Some programming languages have a related control structure, the short-circuit and, written &&, and then, etc.Definition
Logical conjunction is an operation on two logical valueLogical value
In logic and mathematics, a truth value, sometimes called a logical value, is a value indicating the relation of a proposition to truth.In classical logic, with its intended semantics, the truth values are true and false; that is, classical logic is a two-valued logic...
s, typically the values of two proposition
Proposition
In logic and philosophy, the term proposition refers to either the "content" or "meaning" of a meaningful declarative sentence or the pattern of symbols, marks, or sounds that make up a meaningful declarative sentence...
s, that produces a value of true if and only if
IFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
both of its operands are true.
Truth table
The truth tableTruth table
A truth table is a mathematical table used in logic—specifically in connection with Boolean algebra, boolean functions, and propositional calculus—to compute the functional values of logical expressions on each of their functional arguments, that is, on each combination of values taken by their...
of
 :
:| INPUT | OUTPUT | |
| A | B | A AND B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Introduction and elimination rules
As a rule of inference, conjunction introduction is a classically validValidity
In logic, argument is valid if and only if its conclusion is entailed by its premises, a formula is valid if and only if it is true under every interpretation, and an argument form is valid if and only if every argument of that logical form is valid....
, simple argument form. The argument form has two premises, A and B. Intuitively, it permits the inference of their conjunction.
- A,
- B.
- Therefore, A and B.
or in logical operator notation:



Here is an example of an argument that fits the form conjunction introduction
Conjunction introduction
Conjunction introduction is the inference that, if p is true, and q is true, then the conjunction p and q is true.For example, if it's true that it's raining, and it's true that I'm inside, then it's true that "it's raining and I'm inside"....
:
- Bob likes apples.
- Bob likes oranges.
- Therefore, Bob likes apples and oranges.
Conjunction elimination is another classically valid
Validity
In logic, argument is valid if and only if its conclusion is entailed by its premises, a formula is valid if and only if it is true under every interpretation, and an argument form is valid if and only if every argument of that logical form is valid....
, simple argument form. Intuitively, it permits the inference from any conjunction of either element of that conjunction.
- A and B.
- Therefore, A.
...or alternately,
- A and B.
- Therefore, B.
In logical operator notation:


...or alternately,


Properties
commutativityCommutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
: yes
 |
 |
 |
 |
 |
 |
associativity
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
: yes
 |
 |
 |
 |
 |
 |
 |
||
 |
 |
 |
 |
distributivity
Distributivity
In mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
: with various operations, especially with or
Logical disjunction
In logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...
 |
 |
 |
 |
 |
 |
 |
||
 |
 |
 |
 |
| others | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
with exclusive or:
with material nonimplication Material nonimplication Material nonimplication or abjunction is the negation of implication. That is to say that for any two propositions P and Q, if P does not imply Q, then P is the material nonimplication of Q.... :
with itself:
|
idempotency: yes
 |
 |
 |
 |
 |
 |
 |
monotonicity: yes
 |
 |
 |
 |
 |
||
 |
 |
 |
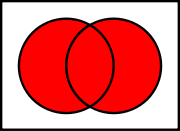
truth-preserving: yes
When all inputs are true, the output is true.
 |
 |
 |
 |
 |
 |
| (to be tested) |
falsehood-preserving: yes
When all inputs are false, the output is false.
 |
 |
 |
 |
 |
 |
| (to be tested) |
Walsh spectrum
Hadamard transform
The Hadamard transform is an example of a generalized class of Fourier transforms...
: (1,-1,-1,1)
Nonlinearity: 1 (the function is bent
Bent function
In the mathematical field of combinatorics, a bent function is a special type of Boolean function. Defined and named in the 1960s by Oscar Rothaus in research not published until 1976, bent functions are so called because they are as different as possible from all linear and affine functions...
)
If using binary
Binary numeral system
The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
values for true (1) and false (0), then logical conjunction works exactly like normal arithmetic multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
.
Applications in computer engineering
In high-level computer programming and digital electronics, logical conjunction is commonly represented by an infix operator, usually as a keyword such as "AND", an algebraic multiplication, or the ampersand symbol "&". Many languages also provide short-circuit control structures corresponding to logical conjunction.Logical conjunction is often used for bitwise operations, where
0 corresponds to false and 1 to true:-
0 AND 0=0, -
0 AND 1=0, -
1 AND 0=0, -
1 AND 1=1.
The operation can also be applied to two binary words viewed as bitstrings of equal length, by taking the bitwise AND of each pair of bits at corresponding positions. For example:
-
11000110 AND 10100011=10000010.
This can be used to select part of a bitstring using a bit mask
Mask (computing)
In computer science, a mask is data that is used for bitwise operations.Using a mask, multiple bits in a byte, nibble, word can be set either on, off or inverted from on to off in a single bitwise operation.-Masking bits to 1:...
. For example,
10011101 AND 00001000 = 00001000 extracts the fifth bit of an 8-bit bitstring.In computer networking, bit masks are used to derive the network address of a subnet
Subnetwork
A subnetwork, or subnet, is a logically visible subdivision of an IP network. The practice of dividing a network into subnetworks is called subnetting....
within an existing network from a given IP address
IP address
An Internet Protocol address is a numerical label assigned to each device participating in a computer network that uses the Internet Protocol for communication. An IP address serves two principal functions: host or network interface identification and location addressing...
, by ANDing the IP address and the subnet mask.
Logical conjunction "
AND" is also used in SQLSQL
SQL is a programming language designed for managing data in relational database management systems ....
operations to form database
Database
A database is an organized collection of data for one or more purposes, usually in digital form. The data are typically organized to model relevant aspects of reality , in a way that supports processes requiring this information...
queries.
The Curry-Howard correspondence relates logical conjunction to product type
Product type
In programming languages and type theory, a product of types is another, compounded, type in a structure. The "operands" of the product are types, and the structure of a product type is determined by the fixed order of the operands in the product. An instance of a product type retains the fixed...
s.
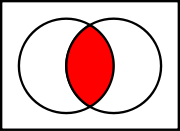
Set-theoretic intersection
The intersectionIntersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
used in set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
is defined in terms of a logical conjunction: x ∈ A ∩ B if and only if (x ∈ A) ∧ (x ∈ B). Because of this, set-theoretic intersection shares several properties with logical conjunction, such as associativity
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
, commutativity
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
, and idempotence
Idempotence
Idempotence is the property of certain operations in mathematics and computer science, that they can be applied multiple times without changing the result beyond the initial application...
.
Natural language
The logical conjunction and in logic is related to, but not the same as, the grammatical conjunctionGrammatical conjunction
In grammar, a conjunction is a part of speech that connects two words, sentences, phrases or clauses together. A discourse connective is a conjunction joining sentences. This definition may overlap with that of other parts of speech, so what constitutes a "conjunction" must be defined for each...
and in natural languages.
English "and" has properties not captured by logical conjunction. For example, "and" sometimes implies order. For example, "They got married and had a child" in common discourse means that the marriage came before the child. The word "and" can also imply a partition of a thing into parts, as "The American flag is red, white, and blue." Here it is not meant that the flag is at once red, white, and blue, but rather that it has a part of each color.


































