Bent function
Encyclopedia
In the mathematical
field of combinatorics
, a bent function is a special type of Boolean function. Defined and named in the 1960s by Oscar Rothaus in research not published until 1976, bent functions are so called because they are as different as possible from all linear and affine functions. They have been extensively studied for their applications in cryptography
, but have also been applied to spread spectrum
, coding theory
, and combinatorial design
. The definition can be extended in several ways, leading to different classes of generalized bent functions that share many of the useful properties of the original.
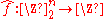given by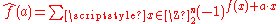
where is the dot product
in Z. Alternatively, let
and
.
Then and hence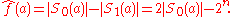
For any Boolean function ƒ and the transform lies in the range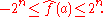
Moreover, the linear function
and the affine function
correspond to the two extreme cases, since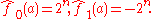
Thus, for each the value of
characterizes where the function ƒ(x) lies in the range from ƒ0(x) to ƒ1(x). Bent functions are in a sense equidistant from all of these, so they are equally hard to approximate with any affine function.
.
The simplest examples of bent functions, written in algebraic normal form
, are F(x1,x2) =
x1x2 and G(x1,x2,x3,x4) =
x1x2 + x3x4. This pattern continues:
x1x2 + x3x4 + ... + xn − 1xn is a bent function for every even n, but there is a wide variety of different types of bent functions as n increases. The sequence of values (−1)ƒ(x), with taken in lexicographical order
, is called a bent sequence; bent functions and bent sequences have equivalent
properties. In this ±1 form, the Walsh transform is easily computed as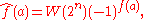
where W(2n) is the natural-ordered Walsh matrix
and the sequence is treated as a column vector.
Rothaus proved that bent functions exist only for even n, and that for a bent function ƒ,
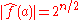for all . In fact, 
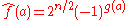, where g is also bent. In this case,
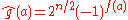, so ƒ and g are considered dual
functions.
Every bent function has a Hamming weight
(number of times it takes the value 1) of 2n − 1 ± 2n/2 − 1, and in fact agrees with any affine function at one of those two numbers of points. So the nonlinearity of ƒ (minimum number of times it equals any affine function) is 2n − 1 − 2n/2 − 1, the maximum possible. Conversely, any Boolean function with nonlinearity 2n − 1 − 2n/2 − 1 is bent. The degree
of ƒ in algebraic normal form (called the nonlinear order of ƒ) is at most n/2 (for n > 2).
Although bent functions are vanishingly rare among Boolean functions of many variables, they come
in many different kinds. There has been detailed research into special classes of bent functions,
such as the homogeneous
ones or those arising from
a monomial
over a finite field
, but so far the bent functions have defied
all attempts at a complete enumeration or classification.
s based on bent functions have
cross-correlation
and autocorrelation
properties rivalling those of the Gold code
s and
Kasami code
s for use in CDMA. These sequences have several applications in
spread spectrum techniques.
The properties of bent functions are naturally of interest in modern digital cryptography
, which seeks to obscure relationships between input and output. By 1988 Forré recognized that the Walsh transform of a function can be used to show that it satisfies the Strict Avalanche Criterion (SAC) and higher-order generalizations, and recommended this tool to select candidates for good S-boxes achieving near-perfect diffusion
. Indeed, the functions satisfying the SAC to the highest possible order are always bent. Furthermore, the bent functions are as far as possible from having what are called linear structures, nonzero vectors a such that ƒ(x+a) + ƒ(x) is a constant. In the language of differential cryptanalysis
(introduced after this property was discovered) the derivative of a bent function ƒ at every nonzero point a (that is, ƒa(x) = ƒ(x+a) + ƒ(x)) is a balanced
Boolean function, taking on each value exactly half of the time. This property is called perfect nonlinearity.
Given such good diffusion properties, apparently perfect resistance to differential cryptanalysis,
and resistance by definition to linear cryptanalysis
, bent functions might at first seem the
ideal choice for secure cryptographic functions such as S-boxes. Their fatal flaw is that they fail to be balanced. In particular, an invertible S-box cannot be constructed directly from bent
functions, and a stream cipher
using a bent combining function is vulnerable to a correlation attack
. Instead, one might start with a bent function and randomly complement appropriate values until the result is balanced. The modified function still has high nonlinearity, and as such functions are very rare the process should be much faster than a brute-force search. But functions produced in this way may lose other desirable properties, even failing to satisfy the SAC—so careful testing is necessary. A number of cryptographers have worked on techniques for generating balanced functions that preserve as many of the good cryptographic qualities of bent functions as possible.
Some of this theoretical research has been incorporated into real cryptographic algorithms. The
CAST design procedure, used by Carlisle Adams
and Stafford Tavares
to construct the S-boxes for the block ciphers CAST-128
and CAST-256
, makes use of bent functions. The cryptographic hash function
HAVAL
uses Boolean functions built from representatives of all four of the equivalence classes of bent functions on six variables. The stream cipher Grain
uses an NLFSR
whose nonlinear feedback polynomial is, by design, the sum of a bent function and a linear function.
type,
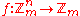such that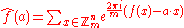
has constant absolute value mn/2. Perfect nonlinear functions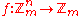
, those such that for all nonzero a, ƒ(x+a) − ƒ(a) takes on each value mn − 1 times, are generalized bent. If m is prime
, the converse is true. In most cases only prime m are considered. For odd prime m, there are generalized bent functions for every positive n, even and odd. They have many of the same good cryptographic properties as the binary bent functions.
Semi-bent functions are an odd-order counterpart to bent functions. A semi-bent function is
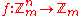with n odd, such that 
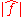takes only the values 0 and m(n+1)/2. They also have good cryptographic characteristics, and some of them are balanced, taking on all possible values equally often.
The partially bent functions form a large class defined by a condition on the Walsh transform and autocorrelation functions. All affine and bent functions are partially bent. This is in turn a proper subclass of the plateaued functions.
The idea behind the hyper-bent functions is to maximize the minimum distance to all Boolean
functions coming from bijective
monomials on the finite field GF(2n), not just the affine functions. For these functions this distance is constant, which may make them resistant to an interpolation attack
.
Other related names have been given to cryptographically important classes of functions , such as almost bent functions and crooked functions. While not Boolean functions themselves, these are closely related to the bent functions and have good nonlinearity properties.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, a bent function is a special type of Boolean function. Defined and named in the 1960s by Oscar Rothaus in research not published until 1976, bent functions are so called because they are as different as possible from all linear and affine functions. They have been extensively studied for their applications in cryptography
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
, but have also been applied to spread spectrum
Spread spectrum
Spread-spectrum techniques are methods by which a signal generated in a particular bandwidth is deliberately spread in the frequency domain, resulting in a signal with a wider bandwidth...
, coding theory
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
, and combinatorial design
Combinatorial design
Combinatorial design theory is the part of combinatorial mathematics that deals with the existence and construction of systems of finite sets whose intersections have specified numerical properties....
. The definition can be extended in several ways, leading to different classes of generalized bent functions that share many of the useful properties of the original.
Walsh transform
Bent functions are defined in terms of the Walsh transform. The Walsh transform of a Boolean function is the function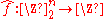 given by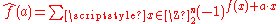where is the dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
in Z. Alternatively, let
and
.
Then and hence
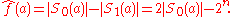
For any Boolean function ƒ and the transform lies in the range
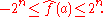
Moreover, the linear function
and the affine function
correspond to the two extreme cases, since
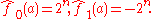
Thus, for each the value of
characterizes where the function ƒ(x) lies in the range from ƒ0(x) to ƒ1(x). Bent functions are in a sense equidistant from all of these, so they are equally hard to approximate with any affine function.Definition and properties
Rothaus defined a bent function as a Boolean function whose Walsh transform has constant absolute valueAbsolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
.
The simplest examples of bent functions, written in algebraic normal form
Algebraic normal form
In Boolean logic, the algebraic normal form is a method of standardizing and normalizing logical formulas. As a normal form, it can be used in automated theorem proving , but is more commonly used in the design of cryptographic random number generators, specifically linear feedback shift registers...
, are F(x1,x2) =
x1x2 and G(x1,x2,x3,x4) =
x1x2 + x3x4. This pattern continues:
x1x2 + x3x4 + ... + xn − 1xn is a bent function for every even n, but there is a wide variety of different types of bent functions as n increases. The sequence of values (−1)ƒ(x), with taken in lexicographical order
Lexicographical order
In mathematics, the lexicographic or lexicographical order, , is a generalization of the way the alphabetical order of words is based on the alphabetical order of letters.-Definition:Given two partially ordered sets A and B, the lexicographical order on...
, is called a bent sequence; bent functions and bent sequences have equivalent
properties. In this ±1 form, the Walsh transform is easily computed as
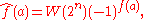
where W(2n) is the natural-ordered Walsh matrix
Walsh matrix
In mathematics, a Walsh matrix is a specific square matrix, with dimensions a power of 2, the entries of which are +1 or −1, and the property that the dot product of any two distinct rows is zero. The Walsh matrix was proposed by Joseph Leonard Walsh in 1923...
and the sequence is treated as a column vector.
Rothaus proved that bent functions exist only for even n, and that for a bent function ƒ,
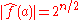for all . In fact, 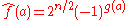, where g is also bent. In this case,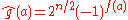, so ƒ and g are considered dualDuality (mathematics)
In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
functions.
Every bent function has a Hamming weight
Hamming weight
The Hamming weight of a string is the number of symbols that are different from the zero-symbol of the alphabet used. It is thus equivalent to the Hamming distance from the all-zero string of the same length. For the most typical case, a string of bits, this is the number of 1's in the string...
(number of times it takes the value 1) of 2n − 1 ± 2n/2 − 1, and in fact agrees with any affine function at one of those two numbers of points. So the nonlinearity of ƒ (minimum number of times it equals any affine function) is 2n − 1 − 2n/2 − 1, the maximum possible. Conversely, any Boolean function with nonlinearity 2n − 1 − 2n/2 − 1 is bent. The degree
Degree of a polynomial
The degree of a polynomial represents the highest degree of a polynominal's terms , should the polynomial be expressed in canonical form . The degree of an individual term is the sum of the exponents acting on the term's variables...
of ƒ in algebraic normal form (called the nonlinear order of ƒ) is at most n/2 (for n > 2).
Although bent functions are vanishingly rare among Boolean functions of many variables, they come
in many different kinds. There has been detailed research into special classes of bent functions,
such as the homogeneous
Homogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
ones or those arising from
a monomial
Monomial
In mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
over a finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
, but so far the bent functions have defied
all attempts at a complete enumeration or classification.
Applications
As early as 1982 it was discovered that maximum length sequenceMaximum length sequence
A maximum length sequence is a type of pseudorandom binary sequence.They are bit sequences generated using maximal linear feedback shift registers and are so called because they are periodic and reproduce every binary sequence that can be reproduced by the shift registers...
s based on bent functions have
cross-correlation
Cross-correlation
In signal processing, cross-correlation is a measure of similarity of two waveforms as a function of a time-lag applied to one of them. This is also known as a sliding dot product or sliding inner-product. It is commonly used for searching a long-duration signal for a shorter, known feature...
and autocorrelation
Autocorrelation
Autocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
properties rivalling those of the Gold code
Gold code
A Gold code, also known as Gold sequence, is a type of binary sequence, used in telecommunication and satellite navigation . Gold codes are named after Robert Gold. Gold codes have bounded small cross-correlations within a set, which is useful when multiple devices are broadcasting in the same range...
s and
Kasami code
Kasami code
Kasami sequences are binary sequences of length 2N-1 where N is an even integer. Kasami sequences have good cross-correlation values approaching the Welch lower bound. There are two classes of Kasami sequences - the small set and the large set....
s for use in CDMA. These sequences have several applications in
spread spectrum techniques.
The properties of bent functions are naturally of interest in modern digital cryptography
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
, which seeks to obscure relationships between input and output. By 1988 Forré recognized that the Walsh transform of a function can be used to show that it satisfies the Strict Avalanche Criterion (SAC) and higher-order generalizations, and recommended this tool to select candidates for good S-boxes achieving near-perfect diffusion
Confusion and diffusion
In cryptography, confusion and diffusion are two properties of the operation of a secure cipher which were identified by Claude Shannon in his paper Communication Theory of Secrecy Systems, published in 1949....
. Indeed, the functions satisfying the SAC to the highest possible order are always bent. Furthermore, the bent functions are as far as possible from having what are called linear structures, nonzero vectors a such that ƒ(x+a) + ƒ(x) is a constant. In the language of differential cryptanalysis
Differential cryptanalysis
Differential cryptanalysis is a general form of cryptanalysis applicable primarily to block ciphers, but also to stream ciphers and cryptographic hash functions. In the broadest sense, it is the study of how differences in an input can affect the resultant difference at the output...
(introduced after this property was discovered) the derivative of a bent function ƒ at every nonzero point a (that is, ƒa(x) = ƒ(x+a) + ƒ(x)) is a balanced
Balanced boolean function
.In mathematics and computer science, a balanced boolean function is a boolean function whose output yields as many 0s as 1s over its input set...
Boolean function, taking on each value exactly half of the time. This property is called perfect nonlinearity.
Given such good diffusion properties, apparently perfect resistance to differential cryptanalysis,
and resistance by definition to linear cryptanalysis
Linear cryptanalysis
In cryptography, linear cryptanalysis is a general form of cryptanalysis based on finding affine approximations to the action of a cipher. Attacks have been developed for block ciphers and stream ciphers...
, bent functions might at first seem the
ideal choice for secure cryptographic functions such as S-boxes. Their fatal flaw is that they fail to be balanced. In particular, an invertible S-box cannot be constructed directly from bent
functions, and a stream cipher
Stream cipher
In cryptography, a stream cipher is a symmetric key cipher where plaintext digits are combined with a pseudorandom cipher digit stream . In a stream cipher the plaintext digits are encrypted one at a time, and the transformation of successive digits varies during the encryption...
using a bent combining function is vulnerable to a correlation attack
Correlation attack
In cryptography, correlation attacks are a class of known plaintext attacks for breaking stream ciphers whose keystream is generated by combining the output of several linear feedback shift registers using a Boolean function...
. Instead, one might start with a bent function and randomly complement appropriate values until the result is balanced. The modified function still has high nonlinearity, and as such functions are very rare the process should be much faster than a brute-force search. But functions produced in this way may lose other desirable properties, even failing to satisfy the SAC—so careful testing is necessary. A number of cryptographers have worked on techniques for generating balanced functions that preserve as many of the good cryptographic qualities of bent functions as possible.
Some of this theoretical research has been incorporated into real cryptographic algorithms. The
CAST design procedure, used by Carlisle Adams
Carlisle Adams
Carlisle M. Adams is a cryptographer and computer security researcher. Formerly senior cryptographer at Entrust, he is currently a professor at the University of Ottawa. His notable work includes the design of the block ciphers CAST-128 and CAST-256. He also helped organize the first Selected...
and Stafford Tavares
Stafford Tavares
Stafford Emanuel Tavares is a cryptographer, professor emeritus at Queen's University.His notable work includes the design of the block ciphers CAST-128 and CAST-256. He also helped organize the first Selected Areas in Cryptography workshop in 1994...
to construct the S-boxes for the block ciphers CAST-128
CAST-128
in cryptography, CAST-128 is a block cipher used in a number of products, notably as the default cipher in some versions of GPG and PGP. It has also been approved for Canadian government use by the Communications Security Establishment...
and CAST-256
CAST-256
In cryptography, CAST-256 is a block cipher published in June 1998. It was submitted as a candidate for the Advanced Encryption Standard ; however, it was not among the five AES finalists. It is an extension of an earlier cipher, CAST-128; both were designed according to the "CAST" design...
, makes use of bent functions. The cryptographic hash function
Cryptographic hash function
A cryptographic hash function is a deterministic procedure that takes an arbitrary block of data and returns a fixed-size bit string, the hash value, such that an accidental or intentional change to the data will change the hash value...
HAVAL
HAVAL
HAVAL is a cryptographic hash function. Unlike MD5, but like most modern cryptographic hash functions, HAVAL can produce hashes of different lengths. HAVAL can produce hashes in lengths of 128 bits, 160 bits, 192 bits, 224 bits, and 256 bits...
uses Boolean functions built from representatives of all four of the equivalence classes of bent functions on six variables. The stream cipher Grain
Grain (cipher)
Grain is a stream cipher submitted to eSTREAM in 2004 by Martin Hell, Thomas Johansson and Willi Meier. It has been selected for the final eSTREAM portfolio for Profile 2 by the eSTREAM project. Grain is designed primarily for restricted hardware environments. It accepts an 80-bit key and a...
uses an NLFSR
NLFSR
A NLFSR is a common component in modern stream ciphers, especially in RFID and smartcard applications. NLFSRs are known to be more resistant to cryptanalytic attacks than Linear Feedback Shift Registers , although construction of large NLFSRs with guaranteed long periods remains an open...
whose nonlinear feedback polynomial is, by design, the sum of a bent function and a linear function.
Generalizations
The most common class of generalized bent functions is the mod mModular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
type,
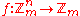such that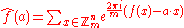has constant absolute value mn/2. Perfect nonlinear functions
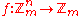, those such that for all nonzero a, ƒ(x+a) − ƒ(a) takes on each value mn − 1 times, are generalized bent. If m is primePrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
, the converse is true. In most cases only prime m are considered. For odd prime m, there are generalized bent functions for every positive n, even and odd. They have many of the same good cryptographic properties as the binary bent functions.
Semi-bent functions are an odd-order counterpart to bent functions. A semi-bent function is
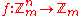with n odd, such that 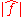takes only the values 0 and m(n+1)/2. They also have good cryptographic characteristics, and some of them are balanced, taking on all possible values equally often.The partially bent functions form a large class defined by a condition on the Walsh transform and autocorrelation functions. All affine and bent functions are partially bent. This is in turn a proper subclass of the plateaued functions.
The idea behind the hyper-bent functions is to maximize the minimum distance to all Boolean
functions coming from bijective
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
monomials on the finite field GF(2n), not just the affine functions. For these functions this distance is constant, which may make them resistant to an interpolation attack
Interpolation attack
In cryptography, an interpolation attack is a type of cryptanalytic attack against block ciphers.In the attack, an algebraic function is used to represent an S-box. This may be a simple quadratic, or a polynomial or rational function over a Galois field. Its coefficients can be determined by...
.
Other related names have been given to cryptographically important classes of functions , such as almost bent functions and crooked functions. While not Boolean functions themselves, these are closely related to the bent functions and have good nonlinearity properties.