Maximum length sequence
Encyclopedia
A maximum length sequence (MLS) is a type of pseudorandom binary sequence.
They are bit sequences generated using maximal linear feedback shift register
s and are so called because they are periodic
and reproduce every binary sequence that can be reproduced by the shift registers (i.e., for length-m registers they produce a sequence of length 2m − 1). A MLS is also sometimes called a n-sequence or a m-sequence. MLSs are spectrally flat
, with the exception of a near-zero DC term.
These sequences may be represented as coefficients of irreducible polynomials in a polynomial ring
over Z/2Z
.
Practical applications for MLS include measuring impulse response
s (e.g., of room reverberation
). They are also used as a basis for deriving pseudo-random sequences in digital communication systems that employ direct-sequence spread spectrum
and frequency-hopping spread spectrum
transmission system
s, and in the efficient design of some fMRI experiments
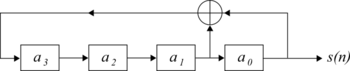MLS are generated using maximal linear feedback shift registers. An MLS-generating system with a shift register of length 4 is shown in Fig. 1. It can be expressed using the following recursive relation:
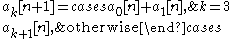
where n is the time index, k is the bit register position, and
represents modulo-2
addition.
As MLS are periodic and shift registers cycle through every possible binary value (with the exception of the zero vector), registers can be initialized to any state, with the exception of the zero vector.
over GF(2) can be associated with the linear feedback shift register. It has degree of the length of the shift register, and has coefficients that are either 0 or 1, corresponding to the taps of the register that feed the xor gate. For example, the polynomial corresponding to Fig. 1 is x4 + x1 + 1.
A necessary and sufficient condition for the sequence generated by a LFSR to be maximal length is that its corresponding polynomial be primitive
.
A "run" is a sub-sequence of "1"s or "0"s within the MLS concerned. The number of runs is the number of such sub-sequences.
function of an MLS is a very close approximation to a train of Kronecker delta function.
(LTI) system's impulse response is to be measured using a MLS, the response can be extracted from the measured system output y[n] by taking its circular cross-correlation with the MLS. This is because the autocorrelation
of a MLS is 1 for zero-lag, and nearly zero (−1/N where N is the sequence length) for all other lags; in other words, the autocorrelation of the MLS can be said to approach unit impulse function as MLS length increases.
If the impulse response of a system is h[n] and the MLS is s[n], then
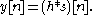
Taking the cross-correlation with respect to s[n] of both sides,
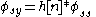
and assuming that φss is an impulse (valid for long sequences)
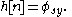
. This relationship allows the correlation
of an MLS to be computed in a fast algorithm similar to the FFT.
They are bit sequences generated using maximal linear feedback shift register
Linear feedback shift register
A linear feedback shift register is a shift register whose input bit is a linear function of its previous state.The most commonly used linear function of single bits is XOR...
s and are so called because they are periodic
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
and reproduce every binary sequence that can be reproduced by the shift registers (i.e., for length-m registers they produce a sequence of length 2m − 1). A MLS is also sometimes called a n-sequence or a m-sequence. MLSs are spectrally flat
Frequency spectrum
The frequency spectrum of a time-domain signal is a representation of that signal in the frequency domain. The frequency spectrum can be generated via a Fourier transform of the signal, and the resulting values are usually presented as amplitude and phase, both plotted versus frequency.Any signal...
, with the exception of a near-zero DC term.
These sequences may be represented as coefficients of irreducible polynomials in a polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
over Z/2Z
Congruence subgroup
In mathematics, a congruence subgroup of a matrix group with integer entries is a subgroup defined by congruence conditions on the entries. A very simple example would be invertible 2x2 integer matrices of determinant 1, such that the off-diagonal entries are even.An importance class of congruence...
.
Practical applications for MLS include measuring impulse response
Impulse response
In signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...
s (e.g., of room reverberation
Reverberation
Reverberation is the persistence of sound in a particular space after the original sound is removed. A reverberation, or reverb, is created when a sound is produced in an enclosed space causing a large number of echoes to build up and then slowly decay as the sound is absorbed by the walls and air...
). They are also used as a basis for deriving pseudo-random sequences in digital communication systems that employ direct-sequence spread spectrum
Direct-sequence spread spectrum
In telecommunications, direct-sequence spread spectrum is a modulation technique. As with other spread spectrum technologies, the transmitted signal takes up more bandwidth than the information signal that is being modulated. The name 'spread spectrum' comes from the fact that the carrier signals...
and frequency-hopping spread spectrum
Frequency-hopping spread spectrum
Frequency-hopping spread spectrum is a method of transmitting radio signals by rapidly switching a carrier among many frequency channels, using a pseudorandom sequence known to both transmitter and receiver...
transmission system
Transmission system
In telecommunications a transmission system is a system that transmits a signal from one place to another. The signal can be an electrical, optical or radio signal....
s, and in the efficient design of some fMRI experiments
Generation of maximum length sequences
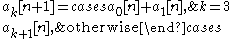
where n is the time index, k is the bit register position, and
represents modulo-2Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
addition.
As MLS are periodic and shift registers cycle through every possible binary value (with the exception of the zero vector), registers can be initialized to any state, with the exception of the zero vector.
Polynomial interpretation
A polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
over GF(2) can be associated with the linear feedback shift register. It has degree of the length of the shift register, and has coefficients that are either 0 or 1, corresponding to the taps of the register that feed the xor gate. For example, the polynomial corresponding to Fig. 1 is x4 + x1 + 1.
A necessary and sufficient condition for the sequence generated by a LFSR to be maximal length is that its corresponding polynomial be primitive
Primitive polynomial
In field theory, a branch of mathematics, a primitive polynomial is the minimal polynomial of a primitive element of the finite extension field GF...
.
Implementation
MLS are inexpensive to implement in hardware or software, and relatively low-order feedback shift registers can generate long sequences; a sequence generated using a shift register of length 20 is 220 − 1 samples long (1,048,575 samples).Properties of maximum length sequences
MLS have the following properties, as formulated by Solomon Golomb.Run property
Of all the "runs" in the sequence of each type (i.e. runs consisting of "1"s and runs consisting of "0"s):- One half of the runs are of length 1.
- One quarter of the runs are of length 2.
- One eighth of the runs are of length 3.
- ... etc. ...
A "run" is a sub-sequence of "1"s or "0"s within the MLS concerned. The number of runs is the number of such sub-sequences.
Correlation property
The autocorrelationAutocorrelation
Autocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
function of an MLS is a very close approximation to a train of Kronecker delta function.
Extraction of impulse responses
If a linear time invariantLTI system theory
Linear time-invariant system theory, commonly known as LTI system theory, comes from applied mathematics and has direct applications in NMR spectroscopy, seismology, circuits, signal processing, control theory, and other technical areas. It investigates the response of a linear and time-invariant...
(LTI) system's impulse response is to be measured using a MLS, the response can be extracted from the measured system output y[n] by taking its circular cross-correlation with the MLS. This is because the autocorrelation
Autocorrelation
Autocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
of a MLS is 1 for zero-lag, and nearly zero (−1/N where N is the sequence length) for all other lags; in other words, the autocorrelation of the MLS can be said to approach unit impulse function as MLS length increases.
If the impulse response of a system is h[n] and the MLS is s[n], then
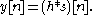
Taking the cross-correlation with respect to s[n] of both sides,
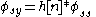
and assuming that φss is an impulse (valid for long sequences)
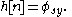
Relationship to Hadamard transform
Cohn and Lempel showed the relationship of the MLS to the Hadamard transformHadamard transform
The Hadamard transform is an example of a generalized class of Fourier transforms...
. This relationship allows the correlation
Correlation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
of an MLS to be computed in a fast algorithm similar to the FFT.
See also
- Impulse responseImpulse responseIn signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...
- Frequency responseFrequency responseFrequency response is the quantitative measure of the output spectrum of a system or device in response to a stimulus, and is used to characterize the dynamics of the system. It is a measure of magnitude and phase of the output as a function of frequency, in comparison to the input...
- Polynomial ringPolynomial ringIn mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
- Federal Standard 1037CFederal Standard 1037CFederal Standard 1037C, titled Telecommunications: Glossary of Telecommunication Terms is a United States Federal Standard, issued by the General Services Administration pursuant to the Federal Property and Administrative Services Act of 1949, as amended....
- Gold codeGold codeA Gold code, also known as Gold sequence, is a type of binary sequence, used in telecommunication and satellite navigation . Gold codes are named after Robert Gold. Gold codes have bounded small cross-correlations within a set, which is useful when multiple devices are broadcasting in the same range...
- Complementary sequencesComplementary sequencesIn applied mathematics, complementary sequences are pairs of sequences with the useful property that their out-of-phase aperiodic autocorrelation coefficients sum to zero. Binary complementary sequences were first introduced by Marcel J. E. Golay in 1949...
External links
- A Little MLS Tutorial — Short on-line tutorial from Robert Bristow-Johnson describing how MLS is used to obtain the impulse responseImpulse responseIn signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...
of a linear time-invariant system. Also describes how nonlinearities in the system can show up as spurious spikes in the apparent impulse response. - Impulse response measurement using MLS — Paper by Jens Hee describing MLS generation. Contains C-code for MLS generation using up to 18-tap-LFSRs and matching Hadamard transform for impulse response extraction.
- Guide to Creation of M-Sequences
- LFSR Reference — Properties of maximal length sequences, and comprehensive feedback tables for maximal lengths from 7 to 16,777,215 (3 to 24 stages), and partial tables for lengths up to 4,294,967,295 (25 to 32 stages).
- A (binaural) room impulse response database generated by means of maximum length sequences