Primitive polynomial
Encyclopedia
In field theory
, a branch of mathematics
, a primitive polynomial is the minimal polynomial
of a primitive element of the finite
extension field GF(pm). In other words, a polynomial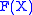
with coefficients in GF(p) = Z/pZ is a primitive polynomial if it has a root 
in GF(pm) such that 
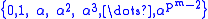is the entire field GF(pm), and moreover, 
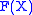is the smallest degree polynomial having 
as root.
In ring theory
, the term primitive polynomial is used for a different purpose, to mean a polynomial over an integral domain R (such as the integer
s) such that no non-invertible element of R divides all its coefficient
s at once. This article will not be concerned with the ring theory usage. See Gauss's lemma
.
, all primitive polynomials are also irreducible.
A primitive polynomial must have a non-zero constant term, for otherwise it will be divisible by x. Over the field of two elements, x+1 is a primitive polynomial and all other primitive polynomials have an odd number of terms, since any polynomial mod 2 with an even number of terms is divisible by x+1.
An irreducible polynomial
of degree m, F(x) over GF(p) for prime p, is a primitive polynomial if the smallest positive integer n such that F(x) divides xn - 1 is n = pm − 1.
Over GF(pm) there are exactly φ(pm − 1)/m primitive polynomials of degree m, where φ is Euler's totient function
.
The roots of a primitive polynomial all have order pm − 1.
. If α in GF(pm) is a root of a primitive polynomial F(x) then since the order of α is pm − 1 that means that all elements of GF(pm) can be represented as successive powers of α:
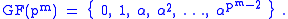
When these elements are reduced modulo F(x) they provide the polynomial basis
representation of all the elements of the field.
Since the multiplicative group
of a finite field is always a cyclic group
, a primitive polynomials f is a polynomial such that x is a generator of the multiplicative group in GF(p)[x]/f(x)
bits. In fact every linear feedback shift register
with maximum cycle (that is 2lfsr length - 1) is related with primitive polynomial.
For example, given the primitive polynomial x10 + x3 + 1, we start with a user-specified bit seed (it need not randomly be chosen, but it can be). We then take the 10th, 3rd, and 0th bits of it, starting from the least significant bit, and xor them together, obtaining a new bit. The seed is then shifted left and the new bit is made the least significant bit of the seed. This process can be repeated to generate 210−1 = 1023 pseudo-random bits.
In general, for a primitive polynomial of degree m, this process will generate 2m−1 pseudo-random bits before repeating the same sequence
(CRC) is an error-detection code that operates by interpreting the message bitstring as the coefficients of a polynomial over GF(2) and dividing it by a fixed generator polynomial also over GF(2); see Mathematics of CRC
. Primitive polynomials, or multiples of them, are a good choice for generator polynomials because they can reliably detect two bit errors that occur far apart in the message bitstring, up to a distance of 2n - 1 for a degree n primitive polynomial.
For trinomials over GF(2), there is a simple test: for every r such that 2r−1 is a Mersenne prime
, a trinomial of degree r is primitive if and only if it is irreducible. Recent algorithms invented by Richard Brent
have enabled the discovery of primitive trinomials over GF(2) of very large degree, such as x6972593 + x3037958 + 1. This can be used to create a pseudo-random number generator of the huge period 26972593−1, or roughly 102098959.
Field theory (mathematics)
Field theory is a branch of mathematics which studies the properties of fields. A field is a mathematical entity for which addition, subtraction, multiplication and division are well-defined....
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a primitive polynomial is the minimal polynomial
Minimal polynomial (field theory)
In field theory, given a field extension E / F and an element α of E that is an algebraic element over F, the minimal polynomial of α is the monic polynomial p, with coefficients in F, of least degree such that p = 0...
of a primitive element of the finite
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
extension field GF(pm). In other words, a polynomial
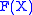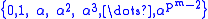with coefficients in GF(p) = Z/pZ is a primitive polynomial if it has a root in GF(pm) such that is the entire field GF(pm), and moreover, 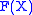is the smallest degree polynomial having as root.In ring theory
Ring theory
In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
, the term primitive polynomial is used for a different purpose, to mean a polynomial over an integral domain R (such as the integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s) such that no non-invertible element of R divides all its coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s at once. This article will not be concerned with the ring theory usage. See Gauss's lemma
Gauss's lemma (polynomial)
In algebra, in the theory of polynomials , Gauss's lemma is either of two related statements about polynomials with integer coefficients:...
.
Properties
Because all minimal polynomials are irreducibleIrreducible polynomial
In mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
, all primitive polynomials are also irreducible.
A primitive polynomial must have a non-zero constant term, for otherwise it will be divisible by x. Over the field of two elements, x+1 is a primitive polynomial and all other primitive polynomials have an odd number of terms, since any polynomial mod 2 with an even number of terms is divisible by x+1.
An irreducible polynomial
Irreducible polynomial
In mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
of degree m, F(x) over GF(p) for prime p, is a primitive polynomial if the smallest positive integer n such that F(x) divides xn - 1 is n = pm − 1.
Over GF(pm) there are exactly φ(pm − 1)/m primitive polynomials of degree m, where φ is Euler's totient function
Euler's totient function
In number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
.
The roots of a primitive polynomial all have order pm − 1.
Field element representation
Primitive polynomials are used in the representation of elements of a finite fieldFinite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
. If α in GF(pm) is a root of a primitive polynomial F(x) then since the order of α is pm − 1 that means that all elements of GF(pm) can be represented as successive powers of α:
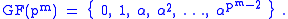
When these elements are reduced modulo F(x) they provide the polynomial basis
Polynomial basis
In mathematics, the polynomial basis is a basis for finite extensions of finite fields.Let α ∈ GF be the root of a primitive polynomial of degree m over GF...
representation of all the elements of the field.
Since the multiplicative group
Multiplicative group
In mathematics and group theory the term multiplicative group refers to one of the following concepts, depending on the context*any group \scriptstyle\mathfrak \,\! whose binary operation is written in multiplicative notation ,*the underlying group under multiplication of the invertible elements of...
of a finite field is always a cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
, a primitive polynomials f is a polynomial such that x is a generator of the multiplicative group in GF(p)[x]/f(x)
Pseudo-Random bit generation
Primitive polynomials define a recurrence relation that can be used to generate pseudorandomPseudorandom number generator
A pseudorandom number generator , also known as a deterministic random bit generator , is an algorithm for generating a sequence of numbers that approximates the properties of random numbers...
bits. In fact every linear feedback shift register
Linear feedback shift register
A linear feedback shift register is a shift register whose input bit is a linear function of its previous state.The most commonly used linear function of single bits is XOR...
with maximum cycle (that is 2lfsr length - 1) is related with primitive polynomial.
For example, given the primitive polynomial x10 + x3 + 1, we start with a user-specified bit seed (it need not randomly be chosen, but it can be). We then take the 10th, 3rd, and 0th bits of it, starting from the least significant bit, and xor them together, obtaining a new bit. The seed is then shifted left and the new bit is made the least significant bit of the seed. This process can be repeated to generate 210−1 = 1023 pseudo-random bits.
In general, for a primitive polynomial of degree m, this process will generate 2m−1 pseudo-random bits before repeating the same sequence
CRC codes
The cyclic redundancy checkCyclic redundancy check
A cyclic redundancy check is an error-detecting code commonly used in digital networks and storage devices to detect accidental changes to raw data...
(CRC) is an error-detection code that operates by interpreting the message bitstring as the coefficients of a polynomial over GF(2) and dividing it by a fixed generator polynomial also over GF(2); see Mathematics of CRC
Mathematics of CRC
The cyclic redundancy check is based on division in the ring of polynomials over the finite field GF , that is, the set of polynomials where each coefficient is either zero or one, and arithmetic operations wrap around .Any string of bits can be interpreted as the coefficients of a message...
. Primitive polynomials, or multiples of them, are a good choice for generator polynomials because they can reliably detect two bit errors that occur far apart in the message bitstring, up to a distance of 2n - 1 for a degree n primitive polynomial.
Primitive trinomials
A useful class of primitive polynomials is the primitive trinomials, those having only three nonzero terms, because they are the simplest and result in the most efficient pseudo-random number generators. A number of results give techniques for locating and testing primitiveness of trinomials.For trinomials over GF(2), there is a simple test: for every r such that 2r−1 is a Mersenne prime
Mersenne prime
In mathematics, a Mersenne number, named after Marin Mersenne , is a positive integer that is one less than a power of two: M_p=2^p-1.\,...
, a trinomial of degree r is primitive if and only if it is irreducible. Recent algorithms invented by Richard Brent
Richard Brent (scientist)
Richard Peirce Brent is an Australian mathematician and computer scientist, born in 1946. He holds the position of Distinguished Professor of Mathematics and Computer Science with a joint appointment in the Mathematical Sciences Institute and the College of Engineering and Computer Science at...
have enabled the discovery of primitive trinomials over GF(2) of very large degree, such as x6972593 + x3037958 + 1. This can be used to create a pseudo-random number generator of the huge period 26972593−1, or roughly 102098959.