Minimal polynomial (field theory)
Encyclopedia
In field theory
, given a field extension
E / F and an element α of E that is an algebraic element
over F, the minimal polynomial of α is the monic polynomial p, with coefficients in F, of least degree such that p(α) = 0. The minimal polynomial is irreducible
over F, and any other non-zero polynomial f with f(α) = 0 is a (polynomial) multiple of p.
Proof: Let E / F be a field extension over F as above,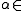
E, and
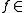F[x] a minimal polynomial. Suppose 
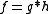where 
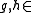F[x]\F. Hence 
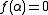. Since fields are also integral domains, we have that 
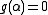or 
. As both the degrees of both 
and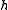 
are smaller than the degree of 
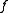, we get a contradiction as 
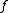does not have a minimal degree. We conclude that minimal polynomials are irreducible.
For example, for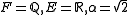
the minimal polynomial for 
is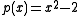 
.
If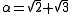
then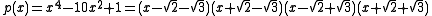
is the minimal polynomial.
The base field F is important as it determines the possibilities for the coefficients of p(x). For instance if we take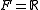
, then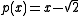
is the minimal polynomial for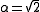
.
Field theory (mathematics)
Field theory is a branch of mathematics which studies the properties of fields. A field is a mathematical entity for which addition, subtraction, multiplication and division are well-defined....
, given a field extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
E / F and an element α of E that is an algebraic element
Algebraic element
In mathematics, if L is a field extension of K, then an element a of L is called an algebraic element over K, or just algebraic over K, if there exists some non-zero polynomial g with coefficients in K such that g=0...
over F, the minimal polynomial of α is the monic polynomial p, with coefficients in F, of least degree such that p(α) = 0. The minimal polynomial is irreducible
Irreducible polynomial
In mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
over F, and any other non-zero polynomial f with f(α) = 0 is a (polynomial) multiple of p.
Proof: Let E / F be a field extension over F as above,
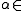E, and 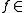F[x] a minimal polynomial. Suppos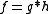e where 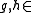F[x]\F. Hence 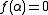. Since fields are also integral domains, we have that 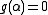or . As both the degrees of both and 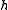are smaller than the degree of 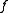, we get a contradiction as 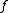does not have a minimal degree. We conclude that minimal polynomials are irreducible.For example, for
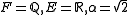the minimal polynomial for is 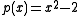.If
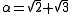
then
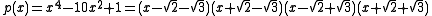
is the minimal polynomial.
The base field F is important as it determines the possibilities for the coefficients of p(x). For instance if we take
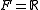, then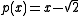is the minimal polynomial for
.
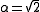