
Field theory (mathematics)
Encyclopedia
Field theory is a branch of mathematics
which studies the properties of field
s. A field is a mathematical entity for which addition, subtraction, multiplication and division are well-defined
.
Please refer to Glossary of field theory
for some basic definitions in field theory.
was used implicitly by Niels Henrik Abel
and Évariste Galois
in their work on the solvability of equations.
In 1871, Richard Dedekind
, called a set of real or complex numbers which is closed under the four arithmetic operations a "field".
In 1881, Leopold Kronecker
defined what he called a "domain of rationality", which is indeed a field of polynomials in modern terms.
In 1893, Heinrich M. Weber gave the first clear definition of an abstract field.
In 1910 Ernst Steinitz
published the very influential paper Algebraische Theorie der Körper (German
: Algebraic Theory of Fields). In this paper he axiomatically studies the properties of fields and defines many important field theoretic concepts like prime field, perfect field
and the transcendence degree
of a field extension
.
Galois, who did not have the term "field" in mind, is honored to be the first mathematician linking group theory
and field theory. Galois theory
is named after him. However it was Emil Artin
who first developed the relationship between groups and fields in great detail during 1928-1942.
s are important objects of study in algebra since they provide a useful generalization of many number systems, such as the rational number
s, real number
s, and complex number
s. In particular, the usual rules of associativity
, commutativity
and distributivity
hold. Fields also appear in many other areas of mathematics; see the examples below.
When abstract algebra was first being developed, the definition of a field usually did not include commutativity of multiplication, and what we today call a field would have been called either a commutative field or a rational domain. In contemporary usage, a field is always commutative. A structure which satisfies all the properties of a field except possibly for commutativity, is today called a division ring
or division algebra or sometimes a skew field. Also non-commutative field is still widely used. In French, fields are called corps (literally, body), skew fields are called corps gauche or anneau à divisions or also algèbre à divisions. The German word for body is Körper and this word is used to denote fields; hence the use of the blackboard bold
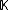 to denote a field.
to denote a field.
The concept of fields was first (implicitly) used to prove that there is no general formula expressing in terms of radicals the roots of a polynomial with rational coefficients of degree 5 or higher.
The aim of Galois theory
is the study of algebraic extensions of a field.
, the separable closure, the cyclic closure et cetera. The idea is always the same: If P is a property of fields, then a P-closure of k is a field K containing k, having property P, and which is minimal in the sense that no proper subfield of K that contains k has property P.
For example if we take P(K) to be the property "every nonconstant polynomial f in K[t] has a root in K", then a P-closure of k is just an algebraic closure
of k.
In general, if P-closures exist for some property P and field k, they are all isomorphic. However, there is in general no preferable isomorphism between two closures.
s and matrices
, two structures in linear algebra
whose components can be elements of an arbitrary field.
Finite field
s are used in number theory
, Galois theory
and coding theory
, and again algebraic extension is an important tool.
Binary fields, fields of characteristic
2, are useful in computer science
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
which studies the properties of field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
s. A field is a mathematical entity for which addition, subtraction, multiplication and division are well-defined
Well-defined
In mathematics, well-definition is a mathematical or logical definition of a certain concept or object which uses a set of base axioms in an entirely unambiguous way and satisfies the properties it is required to satisfy. Usually definitions are stated unambiguously, and it is clear they satisfy...
.
Please refer to Glossary of field theory
Glossary of field theory
Field theory is the branch of mathematics in which fields are studied. This is a glossary of some terms of the subject. -Definition of a field:...
for some basic definitions in field theory.
History
The concept of fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
was used implicitly by Niels Henrik Abel
Niels Henrik Abel
Niels Henrik Abel was a Norwegian mathematician who proved the impossibility of solving the quintic equation in radicals.-Early life:...
and Évariste Galois
Évariste Galois
Évariste Galois was a French mathematician born in Bourg-la-Reine. While still in his teens, he was able to determine a necessary and sufficient condition for a polynomial to be solvable by radicals, thereby solving a long-standing problem...
in their work on the solvability of equations.
In 1871, Richard Dedekind
Richard Dedekind
Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...
, called a set of real or complex numbers which is closed under the four arithmetic operations a "field".
In 1881, Leopold Kronecker
Leopold Kronecker
Leopold Kronecker was a German mathematician who worked on number theory and algebra.He criticized Cantor's work on set theory, and was quoted by as having said, "God made integers; all else is the work of man"...
defined what he called a "domain of rationality", which is indeed a field of polynomials in modern terms.
In 1893, Heinrich M. Weber gave the first clear definition of an abstract field.
In 1910 Ernst Steinitz
Ernst Steinitz
Ernst Steinitz was a German mathematician.- Biography :Steinitz was born in Laurahütte , Silesia, Germany , the son of Sigismund Steinitz, a Jewish coal merchant, and his wife Auguste Cohen; he had two brothers. He studied at the University of Breslau and the University of Berlin, receiving his Ph.D...
published the very influential paper Algebraische Theorie der Körper (German
German language
German is a West Germanic language, related to and classified alongside English and Dutch. With an estimated 90 – 98 million native speakers, German is one of the world's major languages and is the most widely-spoken first language in the European Union....
: Algebraic Theory of Fields). In this paper he axiomatically studies the properties of fields and defines many important field theoretic concepts like prime field, perfect field
Perfect field
In algebra, a field k is said to be perfect if any one of the following equivalent conditions holds:* Every irreducible polynomial over k has distinct roots.* Every polynomial over k is separable.* Every finite extension of k is separable...
and the transcendence degree
Transcendence degree
In abstract algebra, the transcendence degree of a field extension L /K is a certain rather coarse measure of the "size" of the extension...
of a field extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
.
Galois, who did not have the term "field" in mind, is honored to be the first mathematician linking group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
and field theory. Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
is named after him. However it was Emil Artin
Emil Artin
Emil Artin was an Austrian-American mathematician of Armenian descent.-Parents:Emil Artin was born in Vienna to parents Emma Maria, née Laura , a soubrette on the operetta stages of Austria and Germany, and Emil Hadochadus Maria Artin, Austrian-born of Armenian descent...
who first developed the relationship between groups and fields in great detail during 1928-1942.
Introduction
FieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
s are important objects of study in algebra since they provide a useful generalization of many number systems, such as the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s, real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, and complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s. In particular, the usual rules of associativity
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
, commutativity
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
and distributivity
Distributivity
In mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
hold. Fields also appear in many other areas of mathematics; see the examples below.
When abstract algebra was first being developed, the definition of a field usually did not include commutativity of multiplication, and what we today call a field would have been called either a commutative field or a rational domain. In contemporary usage, a field is always commutative. A structure which satisfies all the properties of a field except possibly for commutativity, is today called a division ring
Division ring
In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
or division algebra or sometimes a skew field. Also non-commutative field is still widely used. In French, fields are called corps (literally, body), skew fields are called corps gauche or anneau à divisions or also algèbre à divisions. The German word for body is Körper and this word is used to denote fields; hence the use of the blackboard bold
Blackboard bold
Blackboard bold is a typeface style that is often used for certain symbols in mathematical texts, in which certain lines of the symbol are doubled. The symbols usually denote number sets...
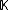 to denote a field.
to denote a field. The concept of fields was first (implicitly) used to prove that there is no general formula expressing in terms of radicals the roots of a polynomial with rational coefficients of degree 5 or higher.
Extensions of a field
An extension of a field k is just a field K containing k as a subfield. One distinguishes between extensions having various qualities. For example, an extension K of a field k is called algebraic, if every element of K is a root of some polynomial with coefficients in k. Otherwise, the extension is called transcendental.The aim of Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
is the study of algebraic extensions of a field.
Closures of a field
Given a field k, various kinds of closures of k may be introduced. For example the algebraic closureAlgebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
, the separable closure, the cyclic closure et cetera. The idea is always the same: If P is a property of fields, then a P-closure of k is a field K containing k, having property P, and which is minimal in the sense that no proper subfield of K that contains k has property P.
For example if we take P(K) to be the property "every nonconstant polynomial f in K[t] has a root in K", then a P-closure of k is just an algebraic closure
Algebraic closure
In mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
of k.
In general, if P-closures exist for some property P and field k, they are all isomorphic. However, there is in general no preferable isomorphism between two closures.
Applications of field theory
The concept of a field is of use, for example, in defining vectorVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s and matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
, two structures in linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
whose components can be elements of an arbitrary field.
Finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s are used in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
and coding theory
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
, and again algebraic extension is an important tool.
Binary fields, fields of characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
2, are useful in computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
.

