
Monic polynomial
Encyclopedia
In algebra
, a monic polynomial is a polynomial

in which the leading coefficient cn is equal to 1.
Univariate polynomials =
If a polynomial
has only one variable ( univariate polynomial ) , then the terms are usually written either from highest degree to lowest degree ("descending powers") or from lowest degree to highest degree ("ascending powers"). A univariate polynomial in x of degree n then takes the general form displayed above, where
are constants, the coefficients of the polynomial.
Here the term cnxn is called the leading term, and its coefficient cn the leading coefficient; if the leading coefficient , the univariate polynomial is called monic.
A and for a given variable x) is closed under multiplication, since the product of the leading terms of two monic polynomials is the leading term of their product. Thus, the monic polynomials form a multiplicative semigroup
of the polynomial ring
A[x]. Actually, since the constant polynomial 1 is monic, this semigroup is even a monoid
.
 (where
(where 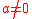 )
)
may be replaced by ,
,
by putting p = b/a and q = c/a. Thus, the equation is equivalent to the monic equation
is equivalent to the monic equation  .
.
coefficients cannot have other rational
solutions than integer solutions. Thus, the equation
possibly might have some rational root, which is not an integer, (and incidently it does have inter alia the root -1/2); while the equations
and
only may have integer solutions or irrational
solutions.
The solutions to monic polynomial equations over an integral domain are important in the theory for integral closures, and hence for algebraic number theory
. In general, assume that A is an integral domain, and also a subring of the integral domain B. Consider the subset C of B, consisting of those B elements, which satisfy monic polynomial equations over A:
The set C contains A, since any a ∈ A satisfies the equation x − a = 0. Moreover, it is possible to prove that C is closed under addition and multiplication. Thus, C is a subring of B. The ring C is called the integral closure of A in B; or just the integral closure of A, if B is the fraction field of A; and the elements of C are said to be integral over A. If here A = Z (the ring of integer
s) and B = C (the field of complex number
s), then C is the ring of algebraic integers.
Multivariate polynomials =
Ordinarily, the term monic is not employed for polynomials of several variables. However, a polynomial in several variables may be regarded as a polynominal in only "the last" variable, but with coefficients being polynomials in the others. This may be done in several ways, depending on which one of the variables is chosen as "the last one". E.g., the real polynomial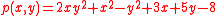
is monic, considered as an element in R[y][x], i.e., as a univariate polynomial in the variable x, with coefficients which themselves are univariate polynomials in y: ;
;
but p(x,y) is not monic as an element in R[x][y], since then the highest degree coefficient (i.e., the y2 coefficient) then is 2x - 1.
There is an alternative convention, which may be useful e.g. in Gröbner basis
contexts: a polynomial is called monic, if its leading coefficient (as a multivariate polynomial) is 1. In other words, assume that p = p(x1,...,xn is a non-zero polynomial in n variables, and that there is a given monomial order on the set of all ("monic") monomials in these variables, i.e., a total order of the free commutative monoid
generated by x1,...,xn, with the unit as lowest element, and respecting multiplication. In that case, this order defines a highest non-vanishing term in p, and p may be called monic, if that term has coefficient one.
"Monic multivariate polynomials" according to this alternative definition share some properties with the "ordinary" (univariate) monic polynomials. Notably, the product of monic polynomials again is monic.
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, a monic polynomial is a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...

in which the leading coefficient cn is equal to 1.
Univariate polynomials =
If a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
has only one variable ( univariate polynomial ) , then the terms are usually written either from highest degree to lowest degree ("descending powers") or from lowest degree to highest degree ("ascending powers"). A univariate polynomial in x of degree n then takes the general form displayed above, where
- cn ≠ 0, cn−1, ..., c2, c1 and c0
are constants, the coefficients of the polynomial.
Here the term cnxn is called the leading term, and its coefficient cn the leading coefficient; if the leading coefficient , the univariate polynomial is called monic.
Multiplicatively closed
The set of all monic polynomials (over a given (unitary) ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
A and for a given variable x) is closed under multiplication, since the product of the leading terms of two monic polynomials is the leading term of their product. Thus, the monic polynomials form a multiplicative semigroup
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
of the polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
A[x]. Actually, since the constant polynomial 1 is monic, this semigroup is even a monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
.
Polynomial equation solutions
In other respects, the properties of monic polynomials and of their corresponding monic polynomial equations depend crucially on the coefficient ring A. If A is a field, then every non-zero polynomial p has exactly one associated monic polynomial q; actually, q is p divided with its leading coefficient. In this manner, then, any non-trivial polynomial equation p(x) = 0 may be replaced by an equivalent monic equation q(x) = 0. E.g., the general real second degree equation (where
(where 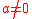 )
)may be replaced by
 ,
,by putting p = b/a and q = c/a. Thus, the equation
 is equivalent to the monic equation
is equivalent to the monic equation  .
.Integrality
On the other hand, if the coefficient ring is not a field, there are more essential differences. E.g., a monic polynomial equation integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
coefficients cannot have other rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
solutions than integer solutions. Thus, the equation

possibly might have some rational root, which is not an integer, (and incidently it does have inter alia the root -1/2); while the equations

and

only may have integer solutions or irrational
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
solutions.
The solutions to monic polynomial equations over an integral domain are important in the theory for integral closures, and hence for algebraic number theory
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
. In general, assume that A is an integral domain, and also a subring of the integral domain B. Consider the subset C of B, consisting of those B elements, which satisfy monic polynomial equations over A:

The set C contains A, since any a ∈ A satisfies the equation x − a = 0. Moreover, it is possible to prove that C is closed under addition and multiplication. Thus, C is a subring of B. The ring C is called the integral closure of A in B; or just the integral closure of A, if B is the fraction field of A; and the elements of C are said to be integral over A. If here A = Z (the ring of integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s) and B = C (the field of complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s), then C is the ring of algebraic integers.
Multivariate polynomials =
Ordinarily, the term monic is not employed for polynomials of several variables. However, a polynomial in several variables may be regarded as a polynominal in only "the last" variable, but with coefficients being polynomials in the others. This may be done in several ways, depending on which one of the variables is chosen as "the last one". E.g., the real polynomial
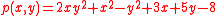
is monic, considered as an element in R[y][x], i.e., as a univariate polynomial in the variable x, with coefficients which themselves are univariate polynomials in y:
 ;
;but p(x,y) is not monic as an element in R[x][y], since then the highest degree coefficient (i.e., the y2 coefficient) then is 2x - 1.
There is an alternative convention, which may be useful e.g. in Gröbner basis
Gröbner basis
In computer algebra, computational algebraic geometry, and computational commutative algebra, a Gröbner basis is a particular kind of generating subset of an ideal I in a polynomial ring R...
contexts: a polynomial is called monic, if its leading coefficient (as a multivariate polynomial) is 1. In other words, assume that p = p(x1,...,xn is a non-zero polynomial in n variables, and that there is a given monomial order on the set of all ("monic") monomials in these variables, i.e., a total order of the free commutative monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
generated by x1,...,xn, with the unit as lowest element, and respecting multiplication. In that case, this order defines a highest non-vanishing term in p, and p may be called monic, if that term has coefficient one.
"Monic multivariate polynomials" according to this alternative definition share some properties with the "ordinary" (univariate) monic polynomials. Notably, the product of monic polynomials again is monic.

