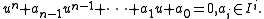Integrality
Encyclopedia
In commutative algebra
, an element b of a commutative ring B is said to be integral over its subring A if there are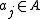 such that
such that
That is to say, b is a root of a monic polynomial over A. If B consists of elements that are integral over A, then B is said to be integral over A or B is an integral extension of A.
If A, B are fields, then the notions of "integral over" and of an "integral extension" are precisely "algebraic over" and "algebraic extensions" in field theory
(since one does not have to insist on "monic".) The special case of greatest interest in number theory
is that of complex numbers integral over Z; in this context, they are usually called algebraic integer
s (e.g.,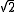 .) A ring consists of some (not all) algebraic integers is called the ring of integers
.) A ring consists of some (not all) algebraic integers is called the ring of integers
, a central object in algebraic number theory
.
In this article, the term ring
will be understood to mean commutative ring
with a unity.
The usual proof of this uses a variant of Cayley–Hamilton theorem
on determinant
s (or simply Cramer's rule
.) Specifically, one can use (Matsumura):
This theorem (with I = A and u multiplication by b) gives (iv)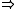 (i) and the rest is easy. (Note the generality on an ideal I is useful for the consideration of the integral closure of an ideal.) Coincidentally, Nakayama's lemma is also an immediate consequence of this theorem.
(i) and the rest is easy. (Note the generality on an ideal I is useful for the consideration of the integral closure of an ideal.) Coincidentally, Nakayama's lemma is also an immediate consequence of this theorem.
It follows from the above that the set of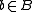 that is integral over A forms a subring of B containing A. It is called the integral closure of A in B. The proof is due to Dedekind (Milne, ANT). Alternatively, one can use symmetric polynomials to show integral elements form a ring. (loc cit.) If A happens to be the integral closure of A, then A is said to be integrally closed in B. If A is reduced
that is integral over A forms a subring of B containing A. It is called the integral closure of A in B. The proof is due to Dedekind (Milne, ANT). Alternatively, one can use symmetric polynomials to show integral elements form a ring. (loc cit.) If A happens to be the integral closure of A, then A is said to be integrally closed in B. If A is reduced
(e.g., a domain) and B its total ring of fractions, one often drops qualification "in B" and simply says "integral closure" and "integrally closed
."
Similarly, "integrality" is transitive. Let C be a ring containing B and c in C. If c is integral over B and B integral over A, then c is integral over A. In particular, if C is itself integral over B and B is integral over A, then C is also integral over A.
If A is noetherian, one has a simpler criterion for integrality: b is integral over A if and only if there is a nonzero d such that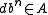 for all
for all 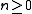 . This can be used to weaken (iii) in the above to
. This can be used to weaken (iii) in the above to
bis There exists a finitely generated A-submodule of B that contains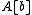 .
.
Finally, the assumption that A be a subring of B can be modified a bit. If f: A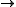 B is a ring homomorphism, then one says f is integral if
B is a ring homomorphism, then one says f is integral if 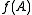 is integral over B, in the same way one says
is integral over B, in the same way one says
f is finite (B finitely generated A-module) or of finite type (B finitely generated A-algebra). In this view point, one can says
Or, more explicitly,
, the lying over property, and the incomparability property. In particular, the Krull dimension
of A and B are the same.
When A, B are domains, A is a field if and only if B is a field.
Let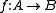 be an integral extension of rings. Then the induced map
be an integral extension of rings. Then the induced map 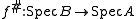 is closed. This is a geometric interpretation of the going-up property.
is closed. This is a geometric interpretation of the going-up property.
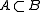 be rings and A the integral closure of A in B. (See above for the definition.)
be rings and A the integral closure of A in B. (See above for the definition.)
Integral closures behave nicely under various construction. Specifically, the localization S−1A is the integral closure of S−1A in S−1B, and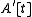 is the integral closure of
is the integral closure of  in
in 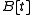 .
.
The integral closure of a local ring A in, say, B, need not be local. This is the case for example when A is Henselian
and B is a field extension of the field of fractions of A.
If A is a subring of a field K (A is necessarily a domain), then the integral closure of A in K is the intersection of all valuation ring
s of K containing A.
Assume A is reduced. The conductor of A is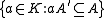 : it is the largest ideal
: it is the largest ideal
of A that is also an ideal of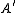 . If the conductor is A, then A is integrally closed. Note this is a generalization of the same concept in algebraic number theory.
. If the conductor is A, then A is integrally closed. Note this is a generalization of the same concept in algebraic number theory.
There is a concept of the integral closure of an ideal. The integral closure of an ideal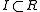 , usually denoted by
, usually denoted by 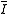 , is the set of all elements
, is the set of all elements 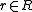 such that there exists a monic polynomial
such that there exists a monic polynomial 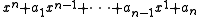 with
with 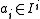 with
with  as a root. The integral closure of an ideal is easily seen to be in the radical
as a root. The integral closure of an ideal is easily seen to be in the radical
of this ideal.
There are alternate definitions as well.
The notion of integral closure of an ideal is used in some proofs of the going-down theorem
.
. Given a field K and a finitely generated K-algebra A, the theorem says it is possible to find elements y1, y2, ..., ym in A that are algebraically independent over K such that A is finite (and hence integral) over B = K[y1,..., ym]. Thus the extension K ⊂ A can be written as a composite K ⊂ B ⊂ A where K ⊂ B is a purely transcendental extension and B ⊂ A is finite.
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
, an element b of a commutative ring B is said to be integral over its subring A if there are
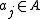 such that
such that
That is to say, b is a root of a monic polynomial over A. If B consists of elements that are integral over A, then B is said to be integral over A or B is an integral extension of A.
If A, B are fields, then the notions of "integral over" and of an "integral extension" are precisely "algebraic over" and "algebraic extensions" in field theory
Field theory (mathematics)
Field theory is a branch of mathematics which studies the properties of fields. A field is a mathematical entity for which addition, subtraction, multiplication and division are well-defined....
(since one does not have to insist on "monic".) The special case of greatest interest in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
is that of complex numbers integral over Z; in this context, they are usually called algebraic integer
Algebraic integer
In number theory, an algebraic integer is a complex number that is a root of some monic polynomial with coefficients in . The set of all algebraic integers is closed under addition and multiplication and therefore is a subring of complex numbers denoted by A...
s (e.g.,
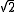 .) A ring consists of some (not all) algebraic integers is called the ring of integers
.) A ring consists of some (not all) algebraic integers is called the ring of integersRing of integers
In mathematics, the ring of integers is the set of integers making an algebraic structure Z with the operations of integer addition, negation, and multiplication...
, a central object in algebraic number theory
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
.
In this article, the term ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
will be understood to mean commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
with a unity.
Examples
- Integers are the only elements of Q that are integral over Z (Thus, Z is the integral closure of Z in Q.)
- Gaussian integerGaussian integerIn number theory, a Gaussian integer is a complex number whose real and imaginary part are both integers. The Gaussian integers, with ordinary addition and multiplication of complex numbers, form an integral domain, usually written as Z[i]. The Gaussian integers are a special case of the quadratic...
s, complex numbers of the form , are integral over Z. (cf. quadratic integerQuadratic integerIn number theory, quadratic integers are a generalization of the rational integers to quadratic fields. Important examples include the Gaussian integers and the Eisenstein integers. Though they have been studied for more than a hundred years, many open problems remain.- Definition :Quadratic...
, are integral over Z. (cf. quadratic integerQuadratic integerIn number theory, quadratic integers are a generalization of the rational integers to quadratic fields. Important examples include the Gaussian integers and the Eisenstein integers. Though they have been studied for more than a hundred years, many open problems remain.- Definition :Quadratic...
s.) is then the integral closure of Z in
is then the integral closure of Z in 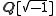 .
. - The roots of unity and nilpotent elements are integral over Z.
- The integral closure of Z in the field of complex numbers C is called the ring of algebraic integerAlgebraic integerIn number theory, an algebraic integer is a complex number that is a root of some monic polynomial with coefficients in . The set of all algebraic integers is closed under addition and multiplication and therefore is a subring of complex numbers denoted by A...
s. - Let a finite group G act on a ring A. Then A is integral over
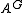 the set of elements fixed by G.
the set of elements fixed by G. - Let R be a ring and u a unit in a ring containing R. Then (i)
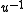 is integral over
is integral over  if and only if
if and only if  (ii)
(ii) 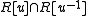 is integral over R.
is integral over R.
Equivalent definitions
Let B be a ring, and let A be a subring of B. Given an element b in B, the following conditions are equivalent:- (i) b is integral over A;
- (ii) the subring A[b] of B generated by A and b is a finitely generated A-module;
- (iii) there exists a subring C of B containing A[b] and which is a finitely-generated A-module;
- (iv) there exists a finitely generated A-submodule M of B with
 and the annihilator of M in B is zero.
and the annihilator of M in B is zero.
The usual proof of this uses a variant of Cayley–Hamilton theorem
Cayley–Hamilton theorem
In linear algebra, the Cayley–Hamilton theorem states that every square matrix over a commutative ring satisfies its own characteristic equation....
on determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
s (or simply Cramer's rule
Cramer's rule
In linear algebra, Cramer's rule is a theorem, which gives an expression for the solution of a system of linear equations with as many equations as unknowns, valid in those cases where there is a unique solution...
.) Specifically, one can use (Matsumura):
- Theorem Let u be an endmorphism of an A-module M generated by n elements and I an ideal of A such that
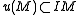 . Then there is a relation:
. Then there is a relation:
-
This theorem (with I = A and u multiplication by b) gives (iv)
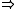 (i) and the rest is easy. (Note the generality on an ideal I is useful for the consideration of the integral closure of an ideal.) Coincidentally, Nakayama's lemma is also an immediate consequence of this theorem.
(i) and the rest is easy. (Note the generality on an ideal I is useful for the consideration of the integral closure of an ideal.) Coincidentally, Nakayama's lemma is also an immediate consequence of this theorem.It follows from the above that the set of
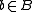 that is integral over A forms a subring of B containing A. It is called the integral closure of A in B. The proof is due to Dedekind (Milne, ANT). Alternatively, one can use symmetric polynomials to show integral elements form a ring. (loc cit.) If A happens to be the integral closure of A, then A is said to be integrally closed in B. If A is reduced
that is integral over A forms a subring of B containing A. It is called the integral closure of A in B. The proof is due to Dedekind (Milne, ANT). Alternatively, one can use symmetric polynomials to show integral elements form a ring. (loc cit.) If A happens to be the integral closure of A, then A is said to be integrally closed in B. If A is reducedReduced ring
In ring theory, a ring R is called a reduced ring if it has no non-zero nilpotent elements. Equivalently, a ring is reduced if it has no non-zero elements with square zero, that is, x2 = 0 implies x = 0...
(e.g., a domain) and B its total ring of fractions, one often drops qualification "in B" and simply says "integral closure" and "integrally closed
Integrally closed domain
In commutative algebra, an integrally closed domain A is an integral domain whose integral closure in the field of fractions of A is A itself...
."
Similarly, "integrality" is transitive. Let C be a ring containing B and c in C. If c is integral over B and B integral over A, then c is integral over A. In particular, if C is itself integral over B and B is integral over A, then C is also integral over A.
If A is noetherian, one has a simpler criterion for integrality: b is integral over A if and only if there is a nonzero d such that
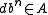 for all
for all 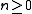 . This can be used to weaken (iii) in the above to
. This can be used to weaken (iii) in the above tobis There exists a finitely generated A-submodule of B that contains
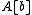 .
.Finally, the assumption that A be a subring of B can be modified a bit. If f: A
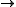 B is a ring homomorphism, then one says f is integral if
B is a ring homomorphism, then one says f is integral if 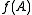 is integral over B, in the same way one says
is integral over B, in the same way one saysf is finite (B finitely generated A-module) or of finite type (B finitely generated A-algebra). In this view point, one can says
- f is finite if and only if f is integral and of finite-type.
Or, more explicitly,
- B is a finitely generated A-module if and only if B is generated as A-algebra by a finite number of elements integral over A.
Integral extensions
One of the Cohen-Seidenberg theorems shows that there is a close relationship between the prime ideals of A and the prime ideals of B. Specifically, they show that an integral extension A⊆B has the going-up propertyGoing up and going down
In commutative algebra, a branch of mathematics, going up and going down are terms which refer to certain properties of chains of prime ideals in integral extensions....
, the lying over property, and the incomparability property. In particular, the Krull dimension
Krull dimension
In commutative algebra, the Krull dimension of a ring R, named after Wolfgang Krull , is the supremum of the number of strict inclusions in a chain of prime ideals. The Krull dimension need not be finite even for a Noetherian ring....
of A and B are the same.
When A, B are domains, A is a field if and only if B is a field.
Let
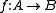 be an integral extension of rings. Then the induced map
be an integral extension of rings. Then the induced map 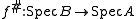 is closed. This is a geometric interpretation of the going-up property.
is closed. This is a geometric interpretation of the going-up property.Integral closure
Let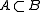 be rings and A the integral closure of A in B. (See above for the definition.)
be rings and A the integral closure of A in B. (See above for the definition.)Integral closures behave nicely under various construction. Specifically, the localization S−1A is the integral closure of S−1A in S−1B, and
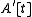 is the integral closure of
is the integral closure of  in
in 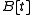 .
.The integral closure of a local ring A in, say, B, need not be local. This is the case for example when A is Henselian
Henselian ring
In mathematics, a Henselian ring is a local ring in which Hensel's lemma holds. They were defined by , who named them after Kurt Hensel.Some standard references for Hensel rings are , , and .-Definitions:...
and B is a field extension of the field of fractions of A.
If A is a subring of a field K (A is necessarily a domain), then the integral closure of A in K is the intersection of all valuation ring
Valuation ring
In abstract algebra, a valuation ring is an integral domain D such that for every element x of its field of fractions F, at least one of x or x −1 belongs to D....
s of K containing A.
Assume A is reduced. The conductor of A is
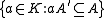 : it is the largest ideal
: it is the largest idealIdeal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
of A that is also an ideal of
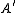 . If the conductor is A, then A is integrally closed. Note this is a generalization of the same concept in algebraic number theory.
. If the conductor is A, then A is integrally closed. Note this is a generalization of the same concept in algebraic number theory.There is a concept of the integral closure of an ideal. The integral closure of an ideal
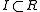 , usually denoted by
, usually denoted by 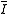 , is the set of all elements
, is the set of all elements 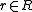 such that there exists a monic polynomial
such that there exists a monic polynomial 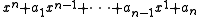 with
with 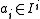 with
with  as a root. The integral closure of an ideal is easily seen to be in the radical
as a root. The integral closure of an ideal is easily seen to be in the radicalRadical of an ideal
In commutative ring theory, a branch of mathematics, the radical of an ideal I is an ideal such that an element x is in the radical if some power of x is in I. A radical ideal is an ideal that is its own radical...
of this ideal.
There are alternate definitions as well.
 if there exists a
if there exists a 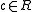 not contained in any minimal prime, such that
not contained in any minimal prime, such that  for all sufficiently large
for all sufficiently large  .
.
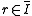 if in the normalized blow-up of
if in the normalized blow-up of 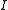 , the pull back of
, the pull back of  is contained in the inverse image of
is contained in the inverse image of 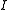 . The blow-up of an ideal is an operation of schemes which replaces the given ideal with a principal ideal. The normalization of a scheme is simply the scheme corresponding to the integral closure of all of its rings.
. The blow-up of an ideal is an operation of schemes which replaces the given ideal with a principal ideal. The normalization of a scheme is simply the scheme corresponding to the integral closure of all of its rings.
The notion of integral closure of an ideal is used in some proofs of the going-down theorem
Going up and going down
In commutative algebra, a branch of mathematics, going up and going down are terms which refer to certain properties of chains of prime ideals in integral extensions....
.
Noether's normalization lemma
Noether's normalisation lemma is a theorem in commutative algebraCommutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
. Given a field K and a finitely generated K-algebra A, the theorem says it is possible to find elements y1, y2, ..., ym in A that are algebraically independent over K such that A is finite (and hence integral) over B = K[y1,..., ym]. Thus the extension K ⊂ A can be written as a composite K ⊂ B ⊂ A where K ⊂ B is a purely transcendental extension and B ⊂ A is finite.