
Quadratic integer
Encyclopedia
In number theory
, quadratic integers are a generalization of the rational integers to quadratic field
s. Important examples include the Gaussian integers and the Eisenstein integers. Though they have been studied for more than a hundred years, many open problems remain.
for integers B and C. Such solutions have the form a + ωb, where a, b are integers, and where ω is defined by;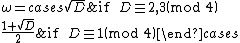
(D is a square-free integer
).
This characterization was first given by Richard Dedekind
in 1871. Fixing a square-free integer D, the quadratic integer ring Z[ω] = {a + ωb : a, b ∈ Z} is a subring of the quadratic field
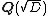 . Moreover, Z[ω] is the integral closure of Z in
. Moreover, Z[ω] is the integral closure of Z in  . In other words, it is the ring of integers
. In other words, it is the ring of integers
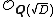 of
of  and thus a Dedekind domain
and thus a Dedekind domain
.
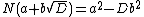 ,
,
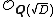 is an Euclidean domain
is an Euclidean domain
(a fortiori, UFD
) when On the other hand, it turned out that
On the other hand, it turned out that 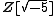 is not a UFD because, for example, 6 has two distinct factorizations into irreducibles:
is not a UFD because, for example, 6 has two distinct factorizations into irreducibles: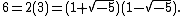
(In fact,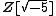 has class number 2.) The failure of the unique factorization led Ernst Kummer
has class number 2.) The failure of the unique factorization led Ernst Kummer
and Dedekind to develop a theory that would enlarge the set of "prime numbers"; the result was the notion of ideals
and the decomposition of ideals by prime ideal
s (cf. splitting of prime ideals in Galois extensions
)
Being a Dedekind domain, a quadratic integer ring is a UFD if and only if it is a principal ideal domain
(i.e., its class number is one.) However, there are quadratic integer rings that are principal ideal domains that are not Euclidean domains. For example,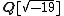 has class number 1 but its ring of integers is not Euclidean. There are effective methods to compute ideal class group
has class number 1 but its ring of integers is not Euclidean. There are effective methods to compute ideal class group
s of quadratic integer rings, but many theoretical questions about their structure are still open after a hundred years.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, quadratic integers are a generalization of the rational integers to quadratic field
Quadratic field
In algebraic number theory, a quadratic field is an algebraic number field K of degree two over Q. It is easy to show that the map d ↦ Q is a bijection from the set of all square-free integers d ≠ 0, 1 to the set of all quadratic fields...
s. Important examples include the Gaussian integers and the Eisenstein integers. Though they have been studied for more than a hundred years, many open problems remain.
Definition
Quadratic integers are solutions of equations of the form:- x2 + Bx + C = 0
for integers B and C. Such solutions have the form a + ωb, where a, b are integers, and where ω is defined by;
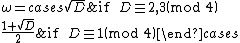
(D is a square-free integer
Square-free integer
In mathematics, a square-free, or quadratfrei, integer is one divisible by no perfect square, except 1. For example, 10 is square-free but 18 is not, as it is divisible by 9 = 32...
).
This characterization was first given by Richard Dedekind
Richard Dedekind
Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...
in 1871. Fixing a square-free integer D, the quadratic integer ring Z[ω] = {a + ωb : a, b ∈ Z} is a subring of the quadratic field
Quadratic field
In algebraic number theory, a quadratic field is an algebraic number field K of degree two over Q. It is easy to show that the map d ↦ Q is a bijection from the set of all square-free integers d ≠ 0, 1 to the set of all quadratic fields...
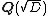 . Moreover, Z[ω] is the integral closure of Z in
. Moreover, Z[ω] is the integral closure of Z in  . In other words, it is the ring of integers
. In other words, it is the ring of integersRing of integers
In mathematics, the ring of integers is the set of integers making an algebraic structure Z with the operations of integer addition, negation, and multiplication...
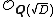 of
of  and thus a Dedekind domain
and thus a Dedekind domainDedekind domain
In abstract algebra, a Dedekind domain or Dedekind ring, named after Richard Dedekind, is an integral domain in which every nonzero proper ideal factors into a product of prime ideals. It can be shown that such a factorization is then necessarily unique up to the order of the factors...
.
Examples
- A classic example is
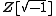 , the Gaussian integerGaussian integerIn number theory, a Gaussian integer is a complex number whose real and imaginary part are both integers. The Gaussian integers, with ordinary addition and multiplication of complex numbers, form an integral domain, usually written as Z[i]. The Gaussian integers are a special case of the quadratic...
, the Gaussian integerGaussian integerIn number theory, a Gaussian integer is a complex number whose real and imaginary part are both integers. The Gaussian integers, with ordinary addition and multiplication of complex numbers, form an integral domain, usually written as Z[i]. The Gaussian integers are a special case of the quadratic...
s, which was introduced by Carl Gauss around 1800 to state his biquadratic reciprocity law. - The elements in
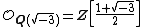 are called Eisenstein integerEisenstein integerIn mathematics, Eisenstein integers , also known as Eulerian integers , are complex numbers of the formz = a + b\omega \,\!where a and b are integers and...
are called Eisenstein integerEisenstein integerIn mathematics, Eisenstein integers , also known as Eulerian integers , are complex numbers of the formz = a + b\omega \,\!where a and b are integers and...
s. - In contrast,
 is not even a Dedekind domainDedekind domainIn abstract algebra, a Dedekind domain or Dedekind ring, named after Richard Dedekind, is an integral domain in which every nonzero proper ideal factors into a product of prime ideals. It can be shown that such a factorization is then necessarily unique up to the order of the factors...
is not even a Dedekind domainDedekind domainIn abstract algebra, a Dedekind domain or Dedekind ring, named after Richard Dedekind, is an integral domain in which every nonzero proper ideal factors into a product of prime ideals. It can be shown that such a factorization is then necessarily unique up to the order of the factors...
.
Class number
Equipped with the normField norm
In mathematics, the norm is a mapping defined in field theory, to map elements of a larger field into a smaller one.-Formal definitions:1. Let K be a field and L a finite extension of K...
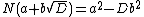 ,
,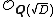 is an Euclidean domain
is an Euclidean domainEuclidean domain
In mathematics, more specifically in abstract algebra and ring theory, a Euclidean domain is a ring that can be endowed with a certain structure – namely a Euclidean function, to be described in detail below – which allows a suitable generalization of the Euclidean algorithm...
(a fortiori, UFD
Unique factorization domain
In mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
) when
 On the other hand, it turned out that
On the other hand, it turned out that 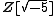 is not a UFD because, for example, 6 has two distinct factorizations into irreducibles:
is not a UFD because, for example, 6 has two distinct factorizations into irreducibles: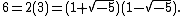
(In fact,
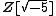 has class number 2.) The failure of the unique factorization led Ernst Kummer
has class number 2.) The failure of the unique factorization led Ernst KummerErnst Kummer
Ernst Eduard Kummer was a German mathematician. Skilled in applied mathematics, Kummer trained German army officers in ballistics; afterwards, he taught for 10 years in a gymnasium, the German equivalent of high school, where he inspired the mathematical career of Leopold Kronecker.-Life:Kummer...
and Dedekind to develop a theory that would enlarge the set of "prime numbers"; the result was the notion of ideals
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
and the decomposition of ideals by prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
s (cf. splitting of prime ideals in Galois extensions
Splitting of prime ideals in Galois extensions
In mathematics, the interplay between the Galois group G of a Galois extension L of a number field K, and the way the prime ideals P of the ring of integers OK factorise as products of prime ideals of OL, provides one of the richest parts of algebraic number theory...
)
Being a Dedekind domain, a quadratic integer ring is a UFD if and only if it is a principal ideal domain
Principal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
(i.e., its class number is one.) However, there are quadratic integer rings that are principal ideal domains that are not Euclidean domains. For example,
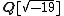 has class number 1 but its ring of integers is not Euclidean. There are effective methods to compute ideal class group
has class number 1 but its ring of integers is not Euclidean. There are effective methods to compute ideal class groupIdeal class group
In mathematics, the extent to which unique factorization fails in the ring of integers of an algebraic number field can be described by a certain group known as an ideal class group...
s of quadratic integer rings, but many theoretical questions about their structure are still open after a hundred years.

