
Gaussian integer
Encyclopedia
In number theory
, a Gaussian integer is a complex number
whose real and imaginary part are both integer
s. The Gaussian integers, with ordinary addition
and multiplication
of complex numbers, form an integral domain, usually written as Z[i]. The Gaussian integers are a special case of the quadratic integer
s. This domain does not have a total order
ing that respects arithmetic.
 Formally, Gaussian integers are the set
Formally, Gaussian integers are the set
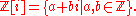
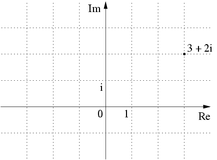
Note that when they are considered within the complex plane
the Gaussian integers may be seen to constitute the 2-dimensional integer lattice
.
The norm
of a Gaussian integer is the natural number
defined as

(Where the overline over "a+bi" refers to the complex conjugate
.)
The norm is multiplicative
, i.e.
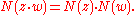
The unit
s of Z[i] are therefore precisely those elements with norm 1, i.e. the elements
with unit
s 1, −1, i, and −i. If x is a Gaussian integer, the four numbers x, ix, −x, and −ix are called the associates of x.
The prime element
s of Z[i] are also known as Gaussian primes. An associate of a Gaussian prime is also a Gaussian prime. The Gaussian primes are symmetric about the real and imaginary axes. The positive integer Gaussian primes are the prime numbers congruent to 3 modulo 4, . One should not refer to only these numbers as "the Gaussian primes", which term refers to all the Gaussian primes, many of which do not lie in Z.
 A Gaussian integer
A Gaussian integer  is a Gaussian prime if and only if either:
is a Gaussian prime if and only if either:
The following elaborates on these conditions.
2 is a special case (in the language of algebraic number theory
, 2 is the only ramified prime in Z[i]).
The integer 2 factors as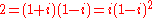 as a Gaussian integer, the second factorisation (in which i is a unit) showing that 2 is divisible by the square of a Gaussian prime; it is the unique prime number with this property.
as a Gaussian integer, the second factorisation (in which i is a unit) showing that 2 is divisible by the square of a Gaussian prime; it is the unique prime number with this property.
The necessary conditions can be stated as following: if a Gaussian integer is a Gaussian prime, then either its norm is a prime number, or its norm is a square of a prime number. This is because for any Gaussian integer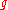 , notice
, notice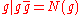 .
.
Here means “divides”; that is,
means “divides”; that is, 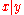 if
if  is a divisor of
is a divisor of 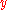 .
.
Now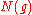 is an integer, and so can be factored as a product
is an integer, and so can be factored as a product  of prime numbers, by the fundamental theorem of arithmetic
of prime numbers, by the fundamental theorem of arithmetic
. By definition of prime element, if is a Gaussian prime, then it divides (in Z[i]) some
is a Gaussian prime, then it divides (in Z[i]) some  . Also,
. Also,  divides
divides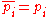 , so
, so 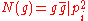 in Z.
in Z.
This gives only two options: either the norm of is a prime number, or the square of a prime number.
is a prime number, or the square of a prime number.
If in fact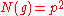 for some prime number
for some prime number  , then both
, then both 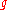 and
and  divide
divide 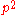 . Neither can be a unit, and so
. Neither can be a unit, and so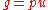 and
and 
where is a unit. This is to say that either
is a unit. This is to say that either  or
or  , where
, where  .
.
However, not every prime number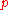 is a Gaussian prime. 2 is not because
is a Gaussian prime. 2 is not because  . Neither are prime numbers of the form
. Neither are prime numbers of the form 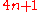 because Fermat's theorem on sums of two squares assures us they can be written
because Fermat's theorem on sums of two squares assures us they can be written  for integers
for integers  and
and  , and
, and 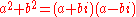 . The only type of prime numbers remaining are of the form
. The only type of prime numbers remaining are of the form  .
.
Prime numbers of the form are also Gaussian primes. For suppose
are also Gaussian primes. For suppose  for
for  , and it can be factored
, and it can be factored  . Then
. Then  . If the factorization is non-trivial, then
. If the factorization is non-trivial, then 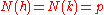 . But no sum of squares of integers can be written
. But no sum of squares of integers can be written  . So the factorization must have been trivial and
. So the factorization must have been trivial and 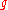 is a Gaussian prime.
is a Gaussian prime.
If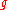 is a Gaussian integer whose norm is a prime number, then
is a Gaussian integer whose norm is a prime number, then 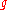 is a Gaussian prime, because the norm is multiplicative.
is a Gaussian prime, because the norm is multiplicative.
of Gaussian rational
s Q(i) consisting of the complex numbers whose real and imaginary part are both rational
.
is within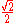 units of a Gaussian integer.
units of a Gaussian integer.
Put another way, every complex number (and hence every Gaussian integer) has a maximal distance of
units to some multiple of z, where z is any Gaussian integer; this turns Z[i] into a Euclidean domain
, where .
.
in his second monograph on quartic reciprocity
(1832) (see http://www.ems-ph.org/journals/show_pdf.php?issn=0013-6018&vol=53&iss=1&rank=2). The theorem of quadratic reciprocity
(which he had first succeeded in proving in 1796) relates the solvability of the congruence x2 ≡ q (mod p) to that of x2 ≡ p (mod q). Similarly, cubic reciprocity relates the solvability of x3 ≡ q (mod p) to that of x3 ≡ p (mod q), and biquadratic (or quartic) reciprocity is a relation between x4 ≡ q (mod p) and x4 ≡ p (mod q). Gauss discovered that the law of biquadratic reciprocity and its supplements were more easily stated and proved as statements about "whole complex numbers" (i.e. the Gaussian integers) than they are as statements about ordinary whole numbers (i.e. the integers).
In a footnote he notes that the Eisenstein integer
s are the natural domain for stating and proving results on cubic reciprocity
and indicates that similar extensions of the integers are the appropriate domains for studying higher reciprocity laws.
This paper not only introduced the Gaussian integers and proved they are a unique factorization domain, it also introduced the terms norm, unit, primary, and associate, which are now standard in algebraic number theory.
There are also conjectures and unsolved problems about the Gaussian primes. Two of them are:
The real and imaginary axes have the infinite set of Gaussian primes 3, 7, 11, 19, ... and their associates. Are there any other lines that have infinitely many Gaussian primes on them? In particular, are there infinitely many Gaussian primes of the form 1+ki?
Is it possible to walk to infinity using the Gaussian primes as stepping stones and taking steps of bounded length? More generally, is there a constant such that the set of Gaussian primes is connected
by edges of length at most , or stated differently, such that for every two Gaussian primes and , the minimax path
in the Gaussian primes between and (the path minimizing the length of its longest edge) has every edge length at most ? The latter statement is slightly stronger than the one about walking to infinity, as it also excludes remote "islands" of Gaussian primes, separated from all others by arbitrarily wide "moats" of Gaussian non-primes.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, a Gaussian integer is a complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
whose real and imaginary part are both integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s. The Gaussian integers, with ordinary addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
and multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
of complex numbers, form an integral domain, usually written as Z[i]. The Gaussian integers are a special case of the quadratic integer
Quadratic integer
In number theory, quadratic integers are a generalization of the rational integers to quadratic fields. Important examples include the Gaussian integers and the Eisenstein integers. Though they have been studied for more than a hundred years, many open problems remain.- Definition :Quadratic...
s. This domain does not have a total order
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
ing that respects arithmetic.

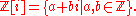
Note that when they are considered within the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
the Gaussian integers may be seen to constitute the 2-dimensional integer lattice
Integer lattice
In mathematics, the n-dimensional integer lattice , denoted Zn, is the lattice in the Euclidean space Rn whose lattice points are n-tuples of integers. The two-dimensional integer lattice is also called the square lattice, or grid lattice. Zn is the simplest example of a root lattice...
.
The norm
Field norm
In mathematics, the norm is a mapping defined in field theory, to map elements of a larger field into a smaller one.-Formal definitions:1. Let K be a field and L a finite extension of K...
of a Gaussian integer is the natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
defined as

(Where the overline over "a+bi" refers to the complex conjugate
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
.)
The norm is multiplicative
Completely multiplicative function
In number theory, functions of positive integers which respect products are important and are called completely multiplicative functions or totally multiplicative functions. Especially in number theory, a weaker condition is also important, respecting only products of coprime numbers, and such...
, i.e.
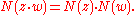
The unit
Unit (ring theory)
In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
s of Z[i] are therefore precisely those elements with norm 1, i.e. the elements
- 1, −1, i and −i.
As a unique factorization domain
The Gaussian integers form a unique factorization domainUnique factorization domain
In mathematics, a unique factorization domain is, roughly speaking, a commutative ring in which every element, with special exceptions, can be uniquely written as a product of prime elements , analogous to the fundamental theorem of arithmetic for the integers...
with unit
Unit (ring theory)
In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
s 1, −1, i, and −i. If x is a Gaussian integer, the four numbers x, ix, −x, and −ix are called the associates of x.
The prime element
Prime element
In abstract algebra, an element p of a commutative ring R is said to be prime if it is not zero, not a unit and whenever p divides ab for some a and b in R, then p divides a or p divides b...
s of Z[i] are also known as Gaussian primes. An associate of a Gaussian prime is also a Gaussian prime. The Gaussian primes are symmetric about the real and imaginary axes. The positive integer Gaussian primes are the prime numbers congruent to 3 modulo 4, . One should not refer to only these numbers as "the Gaussian primes", which term refers to all the Gaussian primes, many of which do not lie in Z.

 is a Gaussian prime if and only if either:
is a Gaussian prime if and only if either:
- one of a, b is zero and the other is a prime number of the form
 (with n a nonnegative integer) or its negative
(with n a nonnegative integer) or its negative  , or
, or - both are nonzero and
 is a prime number (which will not be of the form
is a prime number (which will not be of the form  ).
).
The following elaborates on these conditions.
2 is a special case (in the language of algebraic number theory
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
, 2 is the only ramified prime in Z[i]).
The integer 2 factors as
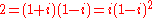 as a Gaussian integer, the second factorisation (in which i is a unit) showing that 2 is divisible by the square of a Gaussian prime; it is the unique prime number with this property.
as a Gaussian integer, the second factorisation (in which i is a unit) showing that 2 is divisible by the square of a Gaussian prime; it is the unique prime number with this property.The necessary conditions can be stated as following: if a Gaussian integer is a Gaussian prime, then either its norm is a prime number, or its norm is a square of a prime number. This is because for any Gaussian integer
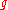 , notice
, notice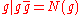 .
.Here
 means “divides”; that is,
means “divides”; that is, 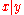 if
if  is a divisor of
is a divisor of 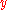 .
.Now
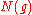 is an integer, and so can be factored as a product
is an integer, and so can be factored as a product  of prime numbers, by the fundamental theorem of arithmetic
of prime numbers, by the fundamental theorem of arithmeticFundamental theorem of arithmetic
In number theory, the fundamental theorem of arithmetic states that any integer greater than 1 can be written as a unique product of prime numbers...
. By definition of prime element, if
 is a Gaussian prime, then it divides (in Z[i]) some
is a Gaussian prime, then it divides (in Z[i]) some  . Also,
. Also,  divides
divides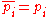 , so
, so 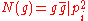 in Z.
in Z.This gives only two options: either the norm of
 is a prime number, or the square of a prime number.
is a prime number, or the square of a prime number.If in fact
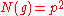 for some prime number
for some prime number  , then both
, then both 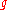 and
and  divide
divide 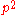 . Neither can be a unit, and so
. Neither can be a unit, and so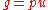 and
and 
where
 is a unit. This is to say that either
is a unit. This is to say that either  or
or  , where
, where  .
.However, not every prime number
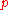 is a Gaussian prime. 2 is not because
is a Gaussian prime. 2 is not because  . Neither are prime numbers of the form
. Neither are prime numbers of the form 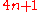 because Fermat's theorem on sums of two squares assures us they can be written
because Fermat's theorem on sums of two squares assures us they can be written  for integers
for integers  and
and  , and
, and 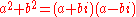 . The only type of prime numbers remaining are of the form
. The only type of prime numbers remaining are of the form  .
.Prime numbers of the form
 are also Gaussian primes. For suppose
are also Gaussian primes. For suppose  for
for  , and it can be factored
, and it can be factored  . Then
. Then  . If the factorization is non-trivial, then
. If the factorization is non-trivial, then 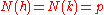 . But no sum of squares of integers can be written
. But no sum of squares of integers can be written  . So the factorization must have been trivial and
. So the factorization must have been trivial and 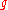 is a Gaussian prime.
is a Gaussian prime.If
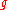 is a Gaussian integer whose norm is a prime number, then
is a Gaussian integer whose norm is a prime number, then 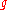 is a Gaussian prime, because the norm is multiplicative.
is a Gaussian prime, because the norm is multiplicative.As an integral closure
The ring of Gaussian integers is the integral closure of Z in the fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
of Gaussian rational
Gaussian rational
In mathematics, a Gaussian rational number is a complex number of the form p + qi, where p and q are both rational numbers....
s Q(i) consisting of the complex numbers whose real and imaginary part are both rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
.
As a Euclidean domain
It is easy to see graphically that every complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
is within
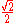 units of a Gaussian integer.
units of a Gaussian integer.Put another way, every complex number (and hence every Gaussian integer) has a maximal distance of

units to some multiple of z, where z is any Gaussian integer; this turns Z[i] into a Euclidean domain
Euclidean domain
In mathematics, more specifically in abstract algebra and ring theory, a Euclidean domain is a ring that can be endowed with a certain structure – namely a Euclidean function, to be described in detail below – which allows a suitable generalization of the Euclidean algorithm...
, where
 .
.Historical background
The ring of Gaussian integers was introduced by Carl Friedrich GaussCarl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
in his second monograph on quartic reciprocity
Quartic reciprocity
Quartic or biquadratic reciprocity is a collection of theorems in elementary and algebraic number theory that state conditions under which the congruence x4 ≡ p is solvable; the word "reciprocity" comes from the form of some of these theorems, in that they relate the solvability of the...
(1832) (see http://www.ems-ph.org/journals/show_pdf.php?issn=0013-6018&vol=53&iss=1&rank=2). The theorem of quadratic reciprocity
Quadratic reciprocity
In number theory, the law of quadratic reciprocity is a theorem about modular arithmetic which gives conditions for the solvability of quadratic equations modulo prime numbers...
(which he had first succeeded in proving in 1796) relates the solvability of the congruence x2 ≡ q (mod p) to that of x2 ≡ p (mod q). Similarly, cubic reciprocity relates the solvability of x3 ≡ q (mod p) to that of x3 ≡ p (mod q), and biquadratic (or quartic) reciprocity is a relation between x4 ≡ q (mod p) and x4 ≡ p (mod q). Gauss discovered that the law of biquadratic reciprocity and its supplements were more easily stated and proved as statements about "whole complex numbers" (i.e. the Gaussian integers) than they are as statements about ordinary whole numbers (i.e. the integers).
In a footnote he notes that the Eisenstein integer
Eisenstein integer
In mathematics, Eisenstein integers , also known as Eulerian integers , are complex numbers of the formz = a + b\omega \,\!where a and b are integers and...
s are the natural domain for stating and proving results on cubic reciprocity
Cubic reciprocity
Cubic reciprocity is a collection of theorems in elementary and algebraic number theory that state conditions under which the congruence x3 ≡ p is solvable; the word "reciprocity" comes from the form of the main theorem, which states that if p and q are primary numbers in the...
and indicates that similar extensions of the integers are the appropriate domains for studying higher reciprocity laws.
This paper not only introduced the Gaussian integers and proved they are a unique factorization domain, it also introduced the terms norm, unit, primary, and associate, which are now standard in algebraic number theory.
Unsolved problems
Gauss's circle problem does not deal with the Gaussian integers per se, but instead asks for the number of lattice points inside a circle of a given radius centered at the origin. This is equivalent to determining the number of Gaussian integers with norm less than a given value.There are also conjectures and unsolved problems about the Gaussian primes. Two of them are:
The real and imaginary axes have the infinite set of Gaussian primes 3, 7, 11, 19, ... and their associates. Are there any other lines that have infinitely many Gaussian primes on them? In particular, are there infinitely many Gaussian primes of the form 1+ki?
Is it possible to walk to infinity using the Gaussian primes as stepping stones and taking steps of bounded length? More generally, is there a constant such that the set of Gaussian primes is connected
Connectedness
In mathematics, connectedness is used to refer to various properties meaning, in some sense, "all one piece". When a mathematical object has such a property, we say it is connected; otherwise it is disconnected...
by edges of length at most , or stated differently, such that for every two Gaussian primes and , the minimax path
Widest path problem
In graph algorithms, the widest path problem, also known as the bottleneck shortest path problem or the maximum capacity path problem, is the problem of finding a path between two designated vertices in a weighted directed graph, maximizing the weight of the minimum-weight edge in the path.For...
in the Gaussian primes between and (the path minimizing the length of its longest edge) has every edge length at most ? The latter statement is slightly stronger than the one about walking to infinity, as it also excludes remote "islands" of Gaussian primes, separated from all others by arbitrarily wide "moats" of Gaussian non-primes.
See also
- Hurwitz quaternionHurwitz quaternionIn mathematics, a Hurwitz quaternion is a quaternion whose components are either all integers or all half-integers...
- Eisenstein integerEisenstein integerIn mathematics, Eisenstein integers , also known as Eulerian integers , are complex numbers of the formz = a + b\omega \,\!where a and b are integers and...
- Dirichlet integer (in French)
- Quadratic integerQuadratic integerIn number theory, quadratic integers are a generalization of the rational integers to quadratic fields. Important examples include the Gaussian integers and the Eisenstein integers. Though they have been studied for more than a hundred years, many open problems remain.- Definition :Quadratic...
- Algebraic integerAlgebraic integerIn number theory, an algebraic integer is a complex number that is a root of some monic polynomial with coefficients in . The set of all algebraic integers is closed under addition and multiplication and therefore is a subring of complex numbers denoted by A...
- Proofs of Fermat's theorem on sums of two squaresProofs of Fermat's theorem on sums of two squaresFermat's theorem on sums of two squares asserts that an odd prime number p can be expressed aswith integer x and y if and only if p is congruent to 1 . The statement was announced by Fermat in 1640, but he supplied no proof....
- Proofs of quadratic reciprocityProofs of quadratic reciprocityIn number theory, the law of quadratic reciprocity, like the Pythagorean theorem, has lent itself to an unusual number of proofs. Several hundred proofs of the law of quadratic reciprocity have been found.-Proofs that are accessible:...
- Splitting of prime ideals in Galois extensionsSplitting of prime ideals in Galois extensionsIn mathematics, the interplay between the Galois group G of a Galois extension L of a number field K, and the way the prime ideals P of the ring of integers OK factorise as products of prime ideals of OL, provides one of the richest parts of algebraic number theory...
describes the structure of prime ideals in the Gaussian integers - Table of Gaussian integer factorizationsTable of Gaussian integer factorizationsGaussian integers may be categorized as zero, the four units, Gaussian primes and composites. This is a list of Gaussian Integers in the first quadrant followed either by an explicit factorization or followed by a label for primes. The factorizations take the form of an optional unit multiplied...
External links
- www.alpertron.com.ar/GAUSSIAN.HTM is a Java applet that evaluates expressions containing Gaussian integers and factors them into Gaussian primes.
- www.alpertron.com.ar/GAUSSPR.HTM is a Java applet that features a graphical view of Gaussian primes.
- Henry G. Baker (1993) Complex Gaussian Integers for 'Gaussian Graphics', ACM SIGPLAN Notices, Vol. 28, Issue 11. DOI 10.1145/165564.165571 (html)
- IMO Compendium text on quadratic extensions and Gaussian Integers in problem solving

