
Algebraic integer
Encyclopedia
In number theory
, an algebraic integer is a complex number
that is a root of some monic polynomial (a polynomial whose leading coefficient is 1) with coefficients in . The set of all algebraic integers is closed under addition and multiplication and therefore is a subring
of complex numbers denoted by A. The ring A is the integral closure of regular integers in complex numbers.
The ring of integers
of a number field K, denoted by OK , is the intersection of K and A: it can also be characterised as the maximal order of the field K.
Each algebraic integer belongs to the ring of integers of some number field. A number x is an algebraic integer if and only if
the ring [x] is finitely generated as an abelian group
, which is to say, as a -module.
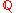 ), in other words,
), in other words, 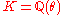 for some
for some 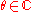 by the primitive element theorem
by the primitive element theorem
.
Algebraic integers are a special case of integral elements of a ring extension. In particular, an algebraic integer is an integral element of a finite extension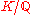 .
.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, an algebraic integer is a complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
that is a root of some monic polynomial (a polynomial whose leading coefficient is 1) with coefficients in . The set of all algebraic integers is closed under addition and multiplication and therefore is a subring
Subring
In mathematics, a subring of R is a subset of a ring, is itself a ring with the restrictions of the binary operations of addition and multiplication of R, and which contains the multiplicative identity of R...
of complex numbers denoted by A. The ring A is the integral closure of regular integers in complex numbers.
The ring of integers
Ring of integers
In mathematics, the ring of integers is the set of integers making an algebraic structure Z with the operations of integer addition, negation, and multiplication...
of a number field K, denoted by OK , is the intersection of K and A: it can also be characterised as the maximal order of the field K.
Each algebraic integer belongs to the ring of integers of some number field. A number x is an algebraic integer if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the ring [x] is finitely generated as an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
, which is to say, as a -module.
Definitions
The following are equivalent definitions of an algebraic integer. Let K be a number field (i.e., a finite extension of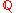 ), in other words,
), in other words, 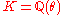 for some
for some 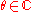 by the primitive element theorem
by the primitive element theoremPrimitive element theorem
In mathematics, more specifically in the area of modern algebra known as field theory, the primitive element theorem or Artin's theorem on primitive elements is a result characterizing the finite degree field extensions that possess a primitive element...
.
-
 is an algebraic integer if there exists a monic polynomial
is an algebraic integer if there exists a monic polynomial  such that
such that 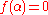 .
. -
 is an algebraic integer if the minimal monic polynomial of
is an algebraic integer if the minimal monic polynomial of  over
over 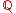 is in
is in  .
. -
 is an algebraic integer if
is an algebraic integer if 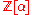 is a finitely generated
is a finitely generated  -module.
-module. -
 is an algebraic integer if there exists a finitely generated
is an algebraic integer if there exists a finitely generated  -submodule
-submodule  such that
such that  .
.
Algebraic integers are a special case of integral elements of a ring extension. In particular, an algebraic integer is an integral element of a finite extension
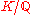 .
.Examples
- The only algebraic integers which are found in the set of rational numbers are the integers. In other words, the intersection of Q and A is exactly Z. The rational number a/b is not an algebraic integer unless b divides a. Note that the leading coefficient of the polynomial bx − a is the integer b. As another special case, the square root √n of a non-negative integer n is an algebraic integer, and so is irrational unless n is a perfect squareSquare numberIn mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...
. - If d is a square free integer then the extension K = Q(√) is a quadratic field of rational numbers. The ring of algebraic integers OK contains √ since this is a root of the monic polynomial x2 − d. Moreover, if d ≡ 1 (mod 4) the element (1 + √)/2 is also an algebraic integer. It satisfies the polynomial x2 − x + (1 − d)/4 where the constant termConstant termIn mathematics, a constant term is a term in an algebraic expression has a value that is constant or cannot change, because it does not contain any modifiable variables. For example, in the quadratic polynomialx^2 + 2x + 3,\ the 3 is a constant term....
(1 − d)/4 is an integer. The full ring of integers is generated by √ or (1 + √)/2 respectively. - If ζn is a primitive n-th root of unityRoot of unityIn mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
, then the ring of integers of the cyclotomic fieldCyclotomic fieldIn number theory, a cyclotomic field is a number field obtained by adjoining a complex primitive root of unity to Q, the field of rational numbers...
Q(ζn) is precisely Z[ζn]. - If α is an algebraic integer then
 is another algebraic integer. A polynomial for β is obtained by substituting xn in the polynomial for α.
is another algebraic integer. A polynomial for β is obtained by substituting xn in the polynomial for α.
Non-example
- If P(x) is a primitive polynomialPrimitive polynomialIn field theory, a branch of mathematics, a primitive polynomial is the minimal polynomial of a primitive element of the finite extension field GF...
which has integer coefficients but is not monic, and P is irreducibleIrreducible polynomialIn mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
over Q, then none of the roots of P are algebraic integers. (Here primitive is used in the sense that the highest common factor of the set of coefficients of P is 1; this is weaker than requiring the coefficients to be pairwise relatively prime.)
Facts
- The sum, difference and product of two algebraic integers is an algebraic integer. In general their quotient is not. The monic polynomial involved is generally of higher degreeDegree (mathematics)In mathematics, there are several meanings of degree depending on the subject.- Unit of angle :A degree , usually denoted by ° , is a measurement of a plane angle, representing 1⁄360 of a turn...
than those of the original algebraic integers, and can be found by taking resultants and factoring. For example, if x2 − x − 1 = 0, y3 − y − 1 = 0 and z = xy, then eliminating x and y from z − xy and the polynomials satisfied by x and y using the resultant gives z6 − 3z4 − 4z3 + z2 + z − 1, which is irreducible, and is the monic polynomial satisfied by the product. (To see that the xy is a root of the x-resultant of z − xy and x2 − x − 1, one might use the fact that the resultant is contained in the ideal generated by its two input polynomials.)
- Any number constructible out of the integers with roots, addition, and multiplication is therefore an algebraic integer; but not all algebraic integers are so constructible: in a naïve sense, most roots of irreducible quintics are not. This is the Abel-Ruffini theorem.
- Every root of a monic polynomial whose coefficients are algebraic integers is itself an algebraic integer. In other words, the algebraic integers form a ring which is integrally closedIntegrally closedIn mathematics, more specifically in abstract algebra, the concept of integrally closed has two meanings, one for groups and one for rings. -Commutative rings:...
in any of its extensions.
- The ring of algebraic integers A is a Bézout domainBézout domainIn mathematics, a Bézout domain is an integral domain in which the sum of two principal ideals is again a principal ideal. This means that for every pair of elements a Bézout identity holds, and that every finitely generated ideal is principal...
.
See also
- Gaussian integerGaussian integerIn number theory, a Gaussian integer is a complex number whose real and imaginary part are both integers. The Gaussian integers, with ordinary addition and multiplication of complex numbers, form an integral domain, usually written as Z[i]. The Gaussian integers are a special case of the quadratic...
- Eisenstein integerEisenstein integerIn mathematics, Eisenstein integers , also known as Eulerian integers , are complex numbers of the formz = a + b\omega \,\!where a and b are integers and...
- Root of unityRoot of unityIn mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
- Dirichlet's unit theoremDirichlet's unit theoremIn mathematics, Dirichlet's unit theorem is a basic result in algebraic number theory due to Gustav Lejeune Dirichlet. It determines the rank of the group of units in the ring OK of algebraic integers of a number field K...
- Fundamental unitsFundamental unit (number theory)In algebraic number theory, a fundamental unit is a generator for the torsion-free unit group of the ring of integers of a number field, when that group is infinite cyclic...

