Order (ring theory)
Encyclopedia
In mathematics
, an order in the sense of ring theory
is a subring
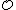of a ring
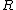that satisfies the conditions
The third condition can be stated more accurately, in terms of the extension of scalars of R to the real number
s, embedding R in a real vector space (equivalently, taking the tensor product over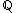
). In less formal terms, additively 
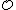should be a free abelian group
generated by a basis for R over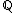
.
The leading example is the case where R is a number field K and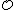
is its ring of integers
. In algebraic number theory
there are examples for any K other than the rational field of proper subrings of the ring of integers that are also orders. For example in the Gaussian integer
s we can take the subring of the
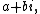
for which b is an even number. A basic result on orders states that the ring of integers in K is the unique maximal order: all other orders in K are contained in it.
When R is not a commutative ring
, the idea of order is still important, but the phenomena are different. For example, the Hurwitz quaternion
s are a maximal order in the quaternion
s with rational co-ordinates; they are not the quaternions with integer coordinates in the most obvious sense. Maximal orders exist in general, but need not be maximum orders: there is in general no largest order, but a number of maximal orders. An important class of examples is that of integral group ring
s.
Because there is a local-global principle for lattices the maximal order question can be examined at a local field
level. This technique is applied in algebraic number theory and modular representation theory
.
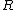in a number field 
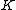is a subring of 
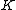which as a 
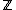-module is finitely generated and of maximal rank 
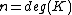(note that we use the "modern" definition of a ring, which includes the existence of the multiplicative identity 
).
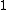Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an order in the sense of ring theory
Ring theory
In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
is a subring
Subring
In mathematics, a subring of R is a subset of a ring, is itself a ring with the restrictions of the binary operations of addition and multiplication of R, and which contains the multiplicative identity of R...
of a ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
that satisfies the conditions- R is a ring which is a finite-dimensional algebra over the rational number field
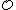spans R over 
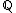, so that 
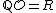, and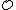
is a lattice in R.
The third condition can be stated more accurately, in terms of the extension of scalars of R to the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, embedding R in a real vector space (equivalently, taking the tensor product over
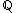). In less formal terms, additively 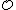should be a free abelian groupFree abelian group
In abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
generated by a basis for R over
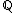.The leading example is the case where R is a number field K and
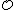is its ring of integersRing of integers
In mathematics, the ring of integers is the set of integers making an algebraic structure Z with the operations of integer addition, negation, and multiplication...
. In algebraic number theory
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
there are examples for any K other than the rational field of proper subrings of the ring of integers that are also orders. For example in the Gaussian integer
Gaussian integer
In number theory, a Gaussian integer is a complex number whose real and imaginary part are both integers. The Gaussian integers, with ordinary addition and multiplication of complex numbers, form an integral domain, usually written as Z[i]. The Gaussian integers are a special case of the quadratic...
s we can take the subring of the
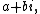
for which b is an even number. A basic result on orders states that the ring of integers in K is the unique maximal order: all other orders in K are contained in it.
When R is not a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
, the idea of order is still important, but the phenomena are different. For example, the Hurwitz quaternion
Hurwitz quaternion
In mathematics, a Hurwitz quaternion is a quaternion whose components are either all integers or all half-integers...
s are a maximal order in the quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
s with rational co-ordinates; they are not the quaternions with integer coordinates in the most obvious sense. Maximal orders exist in general, but need not be maximum orders: there is in general no largest order, but a number of maximal orders. An important class of examples is that of integral group ring
Group ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
s.
Because there is a local-global principle for lattices the maximal order question can be examined at a local field
Local field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
level. This technique is applied in algebraic number theory and modular representation theory
Modular representation theory
Modular representation theory is a branch of mathematics, and that part of representation theory that studies linear representations of finite group G over a field K of positive characteristic...
.
Definition
An order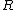 in a number field 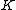is a subring of 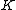which as a 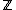-module is finitely generated and of maximal rank 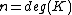(note that we use the "modern" definition of a ring, which includes the existence of the multiplicative identity ).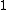