Free abelian group
Encyclopedia
In abstract algebra
, a free abelian group is an abelian group
that has a "basis" in the sense that every element of the group
can be written in one and only one way as a finite linear combination
of elements of the basis, with integer
coefficients. Hence, free abelian groups over a basis B are also known as formal sums over B. Informally, free abelian groups or formal sums may also be seen as signed multiset
s with elements in B.
Free abelian groups have very nice properties which make them similar to vector space
s and allow a general abelian group to be understood as a quotient
of a free abelian group by "relations". Every free abelian group has a rank defined as the cardinality of a basis. The rank determines the group up to isomorphism, and the elements of such a group can be written as finite formal sums of the basis elements. Every subgroup of a free abelian group is itself free abelian, which is important for the description of a general abelian group as a cokernel
of a homomorphism
between free abelian groups.
 of two copies of the infinite cyclic group
of two copies of the infinite cyclic group
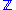
.
Symbolically,
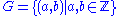 .
.
One basis for this group is {(1,0),(0,1)}.
If we say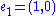 and
and 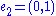 , then we can write the element (4,3) as
, then we can write the element (4,3) as
 . Where 'multiplication' is defined in following way:
. Where 'multiplication' is defined in following way:  .
.
In this basis, there is no other way to write (4,3), but if we choose our basis to be {(1,0),(1,1)}, where and
and 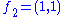 , then we can write (4,3) as
, then we can write (4,3) as
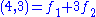 .
.
Unlike vector space
s, not all abelian groups have a basis, hence the special name for those that do.
(For instance, any group having periodic elements is not a free abelian group because any element can be expressed in an infinite number of ways simply by putting in an arbitrary number of cycles constructed from a periodic element.)
The trivial abelian group {0} is also considered to be free abelian, with basis the empty set
.
except in two cases: a free abelian group having an empty basis (rank 0, giving the trivial group
) or having just 1 element in the basis (rank 1, giving the infinite cyclic group). Other abelian groups are not free groups because in free groups ab must be different from ba if a and b are different elements of the basis, while in free abelian groups they must be identical.
Importantly, every subgroup
of a free abelian group is free abelian (see below). As a consequence, to every abelian group A there exists a short exact sequence
with F and G being free abelian (which means that A is isomorphic to the factor group F/G). This is called a free resolution of A. Furthermore, the free abelian groups are precisely the projective objects
in the category of abelian groups
.
It can be surprisingly difficult to determine whether a concretely given group is free abelian. Consider for instance the Baer–Specker group
 , the direct product
, the direct product
(not to be confused with the direct sum, which differs from the direct product on an infinite number of summands) of countably many copies of . Reinhold Baer
. Reinhold Baer
proved in 1937 that this group is not free abelian; Specker proved in 1950 that every countable subgroup of is free abelian.
is free abelian.
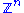 for some natural number
for some natural number
n called the rank of the free abelian group. In general, a free abelian group F has many different bases, but all bases have the same cardinality, and this cardinality is called the rank of F. This rank of free abelian groups can be used to define the rank of all other abelian groups: see rank of an abelian group
. The relationships between different bases can be interesting; for example, the different possibilities for choosing a basis for the free abelian group of rank two is reviewed in the article on the fundamental pair of periods
.
In other words, given a set B, let G be the unique (up to isomorphism) free abelian group with basis B.
For elements and
and 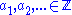 (where there may be an
(where there may be an 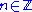 such that
such that  iff
iff
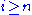 ),
),
that a subgroup of a free group
is free.
Theorem
: Let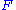 be a free abelian group generated by the set
be a free abelian group generated by the set
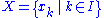 and let
and let 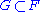 be a subgroup. Then
be a subgroup. Then  is a free abelian group.
is a free abelian group.
Proof
: If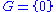 , the statement holds, so we can assume that
, the statement holds, so we can assume that  is nontrivial. First we shall prove this for finite
is nontrivial. First we shall prove this for finite 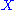 by induction
by induction
. When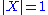 ,
,  is isomorphic to
is isomorphic to 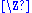 (being nontrivial) and clearly free. Assume that if a group is generated by a set of size
(being nontrivial) and clearly free. Assume that if a group is generated by a set of size  , then every subgroup of it is
, then every subgroup of it is
free. Let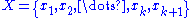 ,
, 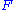 the free group generated by
the free group generated by 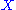 and
and 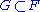 a subgroup. Let
a subgroup. Let 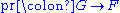 be the projection
be the projection 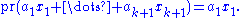 If
If  , then
, then  is a subset of
is a subset of  and free by the induction hypothesis. Thus we can assume that the range is nontrivial. Let
and free by the induction hypothesis. Thus we can assume that the range is nontrivial. Let  be the least such that
be the least such that 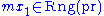 and choose some
and choose some  such that
such that 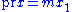 . It
. It
is standard to verify that and if
and if 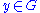 , then
, then  , where
, where  and
and 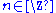 . Hence
. Hence  . By the induction hypothesis
. By the induction hypothesis 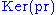 and
and  are free: first is isomorphic to a subgroup of
are free: first is isomorphic to a subgroup of  and the second to
and the second to 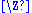 .
.
Assume now that is arbitrary. For each subset
is arbitrary. For each subset  of
of 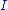 let
let  be the free group generated by
be the free group generated by 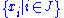 , thus
, thus 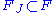 is a free subgroup and denote
is a free subgroup and denote  .
.
Now set
Formally is an injective (one-to-one) map
is an injective (one-to-one) map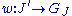
such that generates
generates 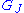 .
.
Clearly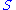 is nonempty: Let us have an element
is nonempty: Let us have an element  in
in  . Then
. Then 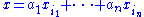 and thus the free group generated by
and thus the free group generated by 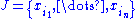 contains
contains  and the intersection
and the intersection 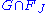 is a nontrivial subgroup of a finitely generated free abelian group and thus free by the induction above.
is a nontrivial subgroup of a finitely generated free abelian group and thus free by the induction above.
If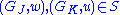 , define order
, define order 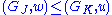 if and only if
if and only if  and the basis
and the basis  is an extension of
is an extension of  ; formally if
; formally if 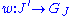 and
and  , then
, then 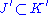 and
and  .
.
If is a
is a  -chain (
-chain (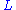 is some linear order) of elements of
is some linear order) of elements of 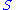 , then obviously
, then obviously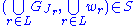 ,
,
so we can apply Zorn's lemma
and conclude that there exists a maximal
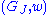 . Since
. Since 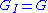 , it is enough to prove now that
, it is enough to prove now that  . Assume on contrary that there is
. Assume on contrary that there is  .
.
Put . If
. If 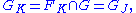 then it means that
then it means that  , but they are not equal, so
, but they are not equal, so 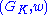 is bigger, which contradicts maximality of
is bigger, which contradicts maximality of 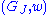 . Otherwise there is an element
. Otherwise there is an element  such that
such that 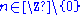 and
and 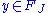 .
.
The set of for which there exists
for which there exists 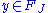 such that
such that  forms a subgroup of
forms a subgroup of  . Let
. Let 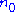 be a generator of this group and let
be a generator of this group and let  with
with  . Now if
. Now if  , then for some
, then for some 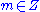 ,
, 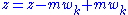 , where
, where 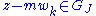 .
.
On the other hand clearly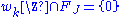 , so
, so  is a basis of
is a basis of  , so
, so  contradicting the maximality again.
contradicting the maximality again. 
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a free abelian group is an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
that has a "basis" in the sense that every element of the group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
can be written in one and only one way as a finite linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of elements of the basis, with integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
coefficients. Hence, free abelian groups over a basis B are also known as formal sums over B. Informally, free abelian groups or formal sums may also be seen as signed multiset
Multiset
In mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...
s with elements in B.
Free abelian groups have very nice properties which make them similar to vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s and allow a general abelian group to be understood as a quotient
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
of a free abelian group by "relations". Every free abelian group has a rank defined as the cardinality of a basis. The rank determines the group up to isomorphism, and the elements of such a group can be written as finite formal sums of the basis elements. Every subgroup of a free abelian group is itself free abelian, which is important for the description of a general abelian group as a cokernel
Cokernel
In mathematics, the cokernel of a linear mapping of vector spaces f : X → Y is the quotient space Y/im of the codomain of f by the image of f....
of a homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
between free abelian groups.
Example
For example, let G be the group that is the direct sum of two copies of the infinite cyclic group
of two copies of the infinite cyclic groupCyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
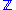
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
.
Symbolically,
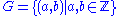 .
.One basis for this group is {(1,0),(0,1)}.
If we say
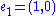 and
and 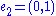 , then we can write the element (4,3) as
, then we can write the element (4,3) as . Where 'multiplication' is defined in following way:
. Where 'multiplication' is defined in following way:  .
.In this basis, there is no other way to write (4,3), but if we choose our basis to be {(1,0),(1,1)}, where
 and
and 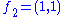 , then we can write (4,3) as
, then we can write (4,3) as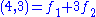 .
.Unlike vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s, not all abelian groups have a basis, hence the special name for those that do.
(For instance, any group having periodic elements is not a free abelian group because any element can be expressed in an infinite number of ways simply by putting in an arbitrary number of cycles constructed from a periodic element.)
The trivial abelian group {0} is also considered to be free abelian, with basis the empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
.
Terminology
Note that a free abelian group is not a free groupFree group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
except in two cases: a free abelian group having an empty basis (rank 0, giving the trivial group
Trivial group
In mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
) or having just 1 element in the basis (rank 1, giving the infinite cyclic group). Other abelian groups are not free groups because in free groups ab must be different from ba if a and b are different elements of the basis, while in free abelian groups they must be identical.
Properties
- For every set B, there exists a free abelian group with basis B, and all such free abelian groups having B as basis are isomorphicGroup isomorphismIn abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
. One example may be constructed as the abelian group of functions on B, where each function may take integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
values, and all but finitely many of its values are zero. This is the direct sum of copies of , one copy for each element of B.
, one copy for each element of B. - If F is a free abelian group with basis B, then we have the following universal propertyUniversal propertyIn various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
: for every arbitrary function f from B to some abelian group A, there exists a unique group homomorphismGroup homomorphismIn mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
from F to A which extends f. This universal property can also be used to define free abelian groups. - Given any abelian group A, there always exists a free abelian group F and a surjective group homomorphism from F to A. This follows from the universal property mentioned above.
- All free abelian groups are torsion-free, and all finitely generated torsion-free abelian groups are free abelian. (The same applies to flatnessFlat moduleIn Homological algebra, and algebraic geometry, a flat module over a ring R is an R-module M such that taking the tensor product over R with M preserves exact sequences. A module is faithfully flat if taking the tensor product with a sequence produces an exact sequence if and only if the original...
, since an abelian group is torsion-free if and only if it is flat.) The additive group of rational numberRational numberIn mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s Q is a (not finitely generated) torsion-free group that's not free abelian. The reason: Q is divisibleDivisible groupIn mathematics, especially in the field of group theory, a divisible group is an abelian group in which every element can, in some sense, be divided by positive integers, or more accurately, every element is an nth multiple for each positive integer n...
but non-zero free abelian groups are never divisible. - Free abelian groups are a special case of free moduleFree moduleIn mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
s, as abelian groups are nothing but modulesModule (mathematics)In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over the ringRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
 .
.
Importantly, every subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of a free abelian group is free abelian (see below). As a consequence, to every abelian group A there exists a short exact sequence
- 0 → G → F → A → 0
with F and G being free abelian (which means that A is isomorphic to the factor group F/G). This is called a free resolution of A. Furthermore, the free abelian groups are precisely the projective objects
Projective module
In mathematics, particularly in abstract algebra and homological algebra, the concept of projective module over a ring R is a more flexible generalisation of the idea of a free module...
in the category of abelian groups
Category of abelian groups
In mathematics, the category Ab has the abelian groups as objects and group homomorphisms as morphisms. This is the prototype of an abelian category....
.
It can be surprisingly difficult to determine whether a concretely given group is free abelian. Consider for instance the Baer–Specker group
Baer–Specker group
In mathematics, in the field of group theory, the Baer–Specker group, or Specker group, is an example of an infinite Abelian group which is a building block in the structure theory of such groups.-Definition:...
 , the direct product
, the direct productDirect product of groups
In the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
(not to be confused with the direct sum, which differs from the direct product on an infinite number of summands) of countably many copies of
 . Reinhold Baer
. Reinhold BaerReinhold Baer
Reinhold Baer was a German mathematician, known for his work in algebra. He introduced injective modules in 1940. He is the eponym of Baer rings....
proved in 1937 that this group is not free abelian; Specker proved in 1950 that every countable subgroup of
 is free abelian.
is free abelian.Rank
Every finitely generated free abelian group is isomorphic to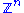 for some natural number
for some natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
n called the rank of the free abelian group. In general, a free abelian group F has many different bases, but all bases have the same cardinality, and this cardinality is called the rank of F. This rank of free abelian groups can be used to define the rank of all other abelian groups: see rank of an abelian group
Rank of an abelian group
In mathematics, the rank, Prüfer rank, or torsion-free rank of an abelian group A is the cardinality of a maximal linearly independent subset. The rank of A determines the size of the largest free abelian group contained in A. If A is torsion-free then it embeds into a vector space over the...
. The relationships between different bases can be interesting; for example, the different possibilities for choosing a basis for the free abelian group of rank two is reviewed in the article on the fundamental pair of periods
Fundamental pair of periods
In mathematics, a fundamental pair of periods is an ordered pair of complex numbers that define a lattice in the complex plane. This type of lattice is the underlying object with which elliptic functions and modular forms are defined....
.
Formal sum
A formal sum of elements of a given set B is an element of the free abelian group with basis B.In other words, given a set B, let G be the unique (up to isomorphism) free abelian group with basis B.
For elements
 and
and 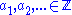 (where there may be an
(where there may be an 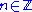 such that
such that  iff
iffIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
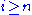 ),
),
Subgroup closure
Every subgroup of a free abelian group is itself a free abelian group. This is similar to the Nielsen–Schreier theoremNielsen–Schreier theorem
In group theory, a branch of mathematics, the Nielsen–Schreier theorem is the statement that every subgroup of a free group is itself free. It is named after Jakob Nielsen and Otto Schreier.-Statement of the theorem:...
that a subgroup of a free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
is free.
Theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
: Let
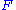 be a free abelian group generated by the set
be a free abelian group generated by the set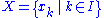 and let
and let 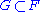 be a subgroup. Then
be a subgroup. Then  is a free abelian group.
is a free abelian group.Proof
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
: If
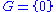 , the statement holds, so we can assume that
, the statement holds, so we can assume that  is nontrivial. First we shall prove this for finite
is nontrivial. First we shall prove this for finite 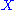 by induction
by inductionMathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
. When
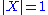 ,
,  is isomorphic to
is isomorphic to 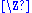 (being nontrivial) and clearly free. Assume that if a group is generated by a set of size
(being nontrivial) and clearly free. Assume that if a group is generated by a set of size  , then every subgroup of it is
, then every subgroup of it isfree. Let
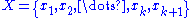 ,
, 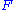 the free group generated by
the free group generated by 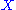 and
and 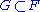 a subgroup. Let
a subgroup. Let 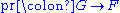 be the projection
be the projection 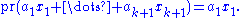 If
If  , then
, then  is a subset of
is a subset of  and free by the induction hypothesis. Thus we can assume that the range is nontrivial. Let
and free by the induction hypothesis. Thus we can assume that the range is nontrivial. Let  be the least such that
be the least such that 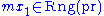 and choose some
and choose some  such that
such that 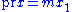 . It
. Itis standard to verify that
 and if
and if 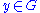 , then
, then  , where
, where  and
and 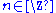 . Hence
. Hence  . By the induction hypothesis
. By the induction hypothesis 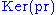 and
and  are free: first is isomorphic to a subgroup of
are free: first is isomorphic to a subgroup of  and the second to
and the second to 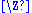 .
.Assume now that
 is arbitrary. For each subset
is arbitrary. For each subset  of
of 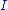 let
let  be the free group generated by
be the free group generated by 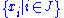 , thus
, thus 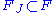 is a free subgroup and denote
is a free subgroup and denote  .
.Now set

Formally
 is an injective (one-to-one) map
is an injective (one-to-one) map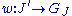
such that
 generates
generates 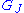 .
.Clearly
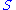 is nonempty: Let us have an element
is nonempty: Let us have an element  in
in  . Then
. Then 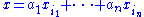 and thus the free group generated by
and thus the free group generated by 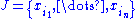 contains
contains  and the intersection
and the intersection 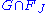 is a nontrivial subgroup of a finitely generated free abelian group and thus free by the induction above.
is a nontrivial subgroup of a finitely generated free abelian group and thus free by the induction above.If
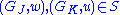 , define order
, define order 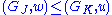 if and only if
if and only if  and the basis
and the basis  is an extension of
is an extension of  ; formally if
; formally if 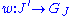 and
and  , then
, then 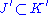 and
and  .
.If
 is a
is a  -chain (
-chain (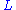 is some linear order) of elements of
is some linear order) of elements of 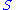 , then obviously
, then obviously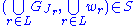 ,
,so we can apply Zorn's lemma
Zorn's lemma
Zorn's lemma, also known as the Kuratowski–Zorn lemma, is a proposition of set theory that states:Suppose a partially ordered set P has the property that every chain has an upper bound in P...
and conclude that there exists a maximal
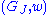 . Since
. Since 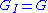 , it is enough to prove now that
, it is enough to prove now that  . Assume on contrary that there is
. Assume on contrary that there is  .
.Put
 . If
. If 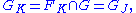 then it means that
then it means that  , but they are not equal, so
, but they are not equal, so 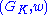 is bigger, which contradicts maximality of
is bigger, which contradicts maximality of 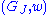 . Otherwise there is an element
. Otherwise there is an element  such that
such that 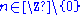 and
and 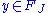 .
.The set of
 for which there exists
for which there exists 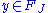 such that
such that  forms a subgroup of
forms a subgroup of  . Let
. Let 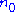 be a generator of this group and let
be a generator of this group and let  with
with  . Now if
. Now if  , then for some
, then for some 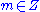 ,
, 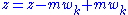 , where
, where 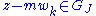 .
.On the other hand clearly
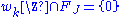 , so
, so  is a basis of
is a basis of  , so
, so  contradicting the maximality again.
contradicting the maximality again.