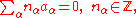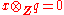Rank of an abelian group
Encyclopedia
In mathematics
, the rank, Prüfer rank, or torsion-free rank of an abelian group
A is the cardinality of a maximal linearly independent subset. The rank of A determines the size of the largest free abelian group
contained in A. If A is torsion-free
then it embeds into a vector space
over the rational numbers of dimension rank A. For finitely generated abelian group
s, rank is a strong invariant and every such group is determined up to isomorphism by its rank and torsion subgroup
. Torsion-free abelian groups of rank 1
have been completely classified. However, the theory of abelian groups of higher rank is more involved.
The term rank has a different meaning in the context of elementary abelian group
s.
where all but finitely many coefficients nα are zero (so that the sum is, in effect, finite), then all coefficients are 0. Any two maximal linearly independent sets in A have the same cardinality, which is called the rank of A.
Rank of an abelian group is analogous to the dimension of a vector space
. The main difference with the case of vector space is a presence of torsion. An element of an abelian group A is classified as torsion if its order
is finite. The set of all torsion elements is a subgroup, called the torsion subgroup
and denoted T(A). A group is called torsion-free if it has no non-trivial torsion elements. The factor-group A/T(A) is the unique maximal torsion-free quotient of A and its rank coincides with the rank of A.
The notion of rank with analogous properties can be defined for modules
over any integral domain, the case of abelian groups corresponds to modules over Z.
, i.e. cannot be expressed as a direct sum of a pair of their proper subgroups. These examples demonstrate that torsion-free abelian group of rank greater than 1 cannot be simply built by direct sums from torsion-free abelian groups of rank 1, whose theory is well-understood. Moreover, for every integer n ≥ 3, there is a torsion-free abelian group of rank 2n−2 that is simultaneously a sum of two indecomposable groups, and a sum of n indecomposable groups. Hence even the number of indecomposable summands of a group of an even rank greater or equal than 4 is not well-defined.
Another result about non-uniqueness of direct sum decompositions is due to A.L.S. Corner: given integers n ≥ k ≥ 1, there exists a torsion-free abelian group A of rank n such that for any partition n = r1 + ... + rk into k natural summands, the group A is the direct sum of k indecomposable subgroups of ranks r1, r2, ..., rk. Thus the sequence of ranks of indecomposable summands in a certain direct sum decomposition of a torsion-free abelian group of finite rank is very far from being an invariant of A.
Other surprising examples include torsion-free rank 2 groups An,m and Bn,m such that An is isomorphic to Bn if and only if n is divisible by m.
For abelian groups of infinite rank, there is an example of a group K and a subgroup G such that
of the module with the field:
It makes sense, since R0 is a field, and thus any module (or, to be more specific, vector space
) over it is free.
It is a generalization, since any abelian group is a module over the integers. It easily follows that the dimension of the product over Q is the cardinality of maximal linearly independent subset, since for any torsion element x and any rational q
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the rank, Prüfer rank, or torsion-free rank of an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
A is the cardinality of a maximal linearly independent subset. The rank of A determines the size of the largest free abelian group
Free abelian group
In abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
contained in A. If A is torsion-free
Torsion-free
In mathematics, the term torsion-free may refer to several unrelated notions:* In abstract algebra, a group is torsion-free if the only element of finite order is the identity....
then it embeds into a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over the rational numbers of dimension rank A. For finitely generated abelian group
Finitely generated abelian group
In abstract algebra, an abelian group is called finitely generated if there exist finitely many elements x1,...,xs in G such that every x in G can be written in the formwith integers n1,...,ns...
s, rank is a strong invariant and every such group is determined up to isomorphism by its rank and torsion subgroup
Torsion subgroup
In the theory of abelian groups, the torsion subgroup AT of an abelian group A is the subgroup of A consisting of all elements that have finite order...
. Torsion-free abelian groups of rank 1
Torsion-free abelian groups of rank 1
Infinitely generated abelian groups have very complex structure and are far less well understood than finitely generated abelian groups. Even torsion-free abelian groups are vastly more varied in their characteristics than vector spaces...
have been completely classified. However, the theory of abelian groups of higher rank is more involved.
The term rank has a different meaning in the context of elementary abelian group
Elementary Abelian group
In group theory, an elementary abelian group is a finite abelian group, where every nontrivial element has order p, where p is a prime; in particular it is a p-group....
s.
Definition
A subset {aα} of an abelian group is linearly independent (over Z) if the only linear combination of these elements that is equal to zero is trivial: ifwhere all but finitely many coefficients nα are zero (so that the sum is, in effect, finite), then all coefficients are 0. Any two maximal linearly independent sets in A have the same cardinality, which is called the rank of A.
Rank of an abelian group is analogous to the dimension of a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
. The main difference with the case of vector space is a presence of torsion. An element of an abelian group A is classified as torsion if its order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
is finite. The set of all torsion elements is a subgroup, called the torsion subgroup
Torsion subgroup
In the theory of abelian groups, the torsion subgroup AT of an abelian group A is the subgroup of A consisting of all elements that have finite order...
and denoted T(A). A group is called torsion-free if it has no non-trivial torsion elements. The factor-group A/T(A) is the unique maximal torsion-free quotient of A and its rank coincides with the rank of A.
The notion of rank with analogous properties can be defined for modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over any integral domain, the case of abelian groups corresponds to modules over Z.
Properties
- The rank of a free abelian groupFree abelian groupIn abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
over a set S is equal to the cardinality of S.
- The rank of an abelian group A coincides with the dimension of the Q-vector space A ⊗ Q. If A is torsion-free then the canonical map A → A ⊗ Q is injective and the rank of A is the minimum dimension of Q-vector space containing A as an abelian subgroup. In particular, any intermediate group Zn < A < Qn has rank n.
- Abelian groups of rank 0 are exactly the periodic abelian groupsPeriodic groupIn group theory, a periodic group or a torsion group is a group in which each element has finite order. All finite groups are periodic. The concept of a periodic group should not be confused with that of a cyclic group, although all finite cyclic groups are periodic.The exponent of a periodic group...
.
- The group Q of rational numbers has rank 1. Torsion-free abelian groups of rank 1Torsion-free abelian groups of rank 1Infinitely generated abelian groups have very complex structure and are far less well understood than finitely generated abelian groups. Even torsion-free abelian groups are vastly more varied in their characteristics than vector spaces...
are realized as subgroups of Q and there is a satisfactory classification of them up to isomorphism. By contrast, there is no satisfactory classification of torsion-free abelian groups of rank 2.
- Rank is additive over short exact sequences: if
- is a s.e.s. of abelian groups then rk B = rk A + rk C. This follows from the flatnessFlat moduleIn Homological algebra, and algebraic geometry, a flat module over a ring R is an R-module M such that taking the tensor product over R with M preserves exact sequences. A module is faithfully flat if taking the tensor product with a sequence produces an exact sequence if and only if the original...
of Q and the corresponding fact for vector spaces.
- Rank is additive over arbitrary direct sumDirect sumIn mathematics, one can often define a direct sum of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets , together with a suitably defined structure. More abstractly, the direct sum is often, but not always, the coproduct in the category in question...
s:
- where the sum in the right hand side uses cardinal arithmetic.
Groups of higher rank
Abelian groups of rank greater than 1 are sources of interesting examples. For instance, for every cardinal d there exist torsion-free abelian groups of rank d that are indecomposableIndecomposable module
In abstract algebra, a module is indecomposable if it is non-zero and cannot be written as a direct sum of two non-zero submodules.Indecomposable is a weaker notion than simple module:simple means "no proper submodule" N...
, i.e. cannot be expressed as a direct sum of a pair of their proper subgroups. These examples demonstrate that torsion-free abelian group of rank greater than 1 cannot be simply built by direct sums from torsion-free abelian groups of rank 1, whose theory is well-understood. Moreover, for every integer n ≥ 3, there is a torsion-free abelian group of rank 2n−2 that is simultaneously a sum of two indecomposable groups, and a sum of n indecomposable groups. Hence even the number of indecomposable summands of a group of an even rank greater or equal than 4 is not well-defined.
Another result about non-uniqueness of direct sum decompositions is due to A.L.S. Corner: given integers n ≥ k ≥ 1, there exists a torsion-free abelian group A of rank n such that for any partition n = r1 + ... + rk into k natural summands, the group A is the direct sum of k indecomposable subgroups of ranks r1, r2, ..., rk. Thus the sequence of ranks of indecomposable summands in a certain direct sum decomposition of a torsion-free abelian group of finite rank is very far from being an invariant of A.
Other surprising examples include torsion-free rank 2 groups An,m and Bn,m such that An is isomorphic to Bn if and only if n is divisible by m.
For abelian groups of infinite rank, there is an example of a group K and a subgroup G such that
- K is indecomposable;
- K is generated by G and a single other element; and
- Every nonzero direct summand of G is decomposable.
Generalization
The notion of rank can be generalized for any module M over an integral domain R, as the dimension over R0, the quotient field, of the tensor productTensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
of the module with the field:
It makes sense, since R0 is a field, and thus any module (or, to be more specific, vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
) over it is free.
It is a generalization, since any abelian group is a module over the integers. It easily follows that the dimension of the product over Q is the cardinality of maximal linearly independent subset, since for any torsion element x and any rational q