Torsion subgroup
Encyclopedia
In the theory of abelian group
s, the torsion subgroup AT of an abelian group A is the subgroup
of A consisting of all elements that have finite order
. An abelian group A is called a torsion (or periodic
) group if every element of A has finite order and is called torsion-free if every element of A except the identity
is of infinite order.
The proof that AT is closed under addition relies on the commutativity of addition (see examples section).
If A is abelian, then the torsion subgroup T is a fully characteristic subgroup
of A and the factor group A/T is torsion-free. There is a covariant functor from the category of abelian groups
to the category of torsion groups that sends every group to its torsion subgroup and every homomorphism to its restriction to the torsion subgroup. There is another covariant functor from the category of abelian groups to the category of torsion-free groups that sends every group to its quotient by its torsion subgroup, and sends every homomorphism to the obvious induced homomorphism (which is easily seen to be well-defined).
If A is finitely generated and abelian, then it can be written as the direct sum of its torsion subgroup T and a torsion-free subgroup (but this is not true for all infinitely generated abelian groups). In any decomposition of A as a direct sum of a torsion subgroup S and a torsion-free subgroup, S must equal T (but the torsion-free subgroup is not uniquely determined). This is a key step in the classification of finitely generated abelian group
s.
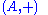and any prime number p the set ATp of elements of A that have order a power of p is a subgroup called the p-power torsion subgroup or, more loosely, the p-torsion subgroup:
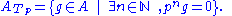
The torsion subgroup AT is isomorphic to the direct sum of its p-power torsion subgroups over all prime numbers p:
When A is a finite abelian group, ATp coincides with the unique Sylow p-subgroup of A.
Each p-power torsion subgroup of A is a fully characteristic subgroup
. More strongly, any homomorphism between abelian groups sends each p-power torsion subgroup into the corresponding p-power torsion subgroup.
For each prime number p, this provides a functor
from the category of abelian groups to the category of p-power torsion groups that sends every group to its p-power torsion subgroup, and restricts every homomorphism to the p-torsion subgroups. The product over the set of all prime numbers of the restriction of these functors to the category of torsion groups, is a faithful functor from the category of torsion groups to the product over all prime numbers of the categories of p-torsion groups. In a sense, this means that studying p-torsion groups in isolation tells us everything about torsion groups in general.
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s, the torsion subgroup AT of an abelian group A is the subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of A consisting of all elements that have finite order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
. An abelian group A is called a torsion (or periodic
Periodic group
In group theory, a periodic group or a torsion group is a group in which each element has finite order. All finite groups are periodic. The concept of a periodic group should not be confused with that of a cyclic group, although all finite cyclic groups are periodic.The exponent of a periodic group...
) group if every element of A has finite order and is called torsion-free if every element of A except the identity
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
is of infinite order.
The proof that AT is closed under addition relies on the commutativity of addition (see examples section).
If A is abelian, then the torsion subgroup T is a fully characteristic subgroup
Characteristic subgroup
In mathematics, particularly in the area of abstract algebra known as group theory, a characteristic subgroup is a subgroup that is invariant under all automorphisms of the parent group. Because conjugation is an automorphism, every characteristic subgroup is normal, though not every normal...
of A and the factor group A/T is torsion-free. There is a covariant functor from the category of abelian groups
Category of abelian groups
In mathematics, the category Ab has the abelian groups as objects and group homomorphisms as morphisms. This is the prototype of an abelian category....
to the category of torsion groups that sends every group to its torsion subgroup and every homomorphism to its restriction to the torsion subgroup. There is another covariant functor from the category of abelian groups to the category of torsion-free groups that sends every group to its quotient by its torsion subgroup, and sends every homomorphism to the obvious induced homomorphism (which is easily seen to be well-defined).
If A is finitely generated and abelian, then it can be written as the direct sum of its torsion subgroup T and a torsion-free subgroup (but this is not true for all infinitely generated abelian groups). In any decomposition of A as a direct sum of a torsion subgroup S and a torsion-free subgroup, S must equal T (but the torsion-free subgroup is not uniquely determined). This is a key step in the classification of finitely generated abelian group
Finitely generated abelian group
In abstract algebra, an abelian group is called finitely generated if there exist finitely many elements x1,...,xs in G such that every x in G can be written in the formwith integers n1,...,ns...
s.
p-power torsion subgroups
For any abelian group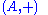 and any prime number p the set ATp of elements of A that have order a power of p is a subgroup called the p-power torsion subgroup or, more loosely, the p-torsion subgroup: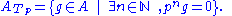The torsion subgroup AT is isomorphic to the direct sum of its p-power torsion subgroups over all prime numbers p:
When A is a finite abelian group, ATp coincides with the unique Sylow p-subgroup of A.
Each p-power torsion subgroup of A is a fully characteristic subgroup
Characteristic subgroup
In mathematics, particularly in the area of abstract algebra known as group theory, a characteristic subgroup is a subgroup that is invariant under all automorphisms of the parent group. Because conjugation is an automorphism, every characteristic subgroup is normal, though not every normal...
. More strongly, any homomorphism between abelian groups sends each p-power torsion subgroup into the corresponding p-power torsion subgroup.
For each prime number p, this provides a functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
from the category of abelian groups to the category of p-power torsion groups that sends every group to its p-power torsion subgroup, and restricts every homomorphism to the p-torsion subgroups. The product over the set of all prime numbers of the restriction of these functors to the category of torsion groups, is a faithful functor from the category of torsion groups to the product over all prime numbers of the categories of p-torsion groups. In a sense, this means that studying p-torsion groups in isolation tells us everything about torsion groups in general.
Examples and further results
- The torsion subset of a non-abelian group is not, in general, a subgroup. For example, in the infinite dihedral groupInfinite dihedral groupIn mathematics, the infinite dihedral group Dih∞ is an infinite group with properties analogous to those of the finite dihedral groups.-Definition:...
, which has presentationPresentation of a groupIn mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
:
- < x, y | x² = y² = 1 >
- the element xy is a product of two torsion elements, but has infinite order.
- The torsion elements in a nilpotent groupNilpotent groupIn mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...
form a normal subgroup.
- The torsion elements in a nilpotent group
- Obviously, every finite abelian group is a torsion group. Not every torsion group is finite however: consider the direct sum of a countable number of copies of the cyclic groupCyclic groupIn group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
C2; this is a torsion group since every element has order 2. Nor need there be an upper bound on the orders of elements in a torsion group if it isn't finitely generatedGenerating set of a groupIn abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
, as the example of the factor group Q/Z shows.
- Every free abelian groupFree abelian groupIn abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
is torsion-free, but the converse is not true, as is shown by the additive group of the rational numberRational numberIn mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s Q.
- Even if A is not finitely generated, the size of its torsion-free part is uniquely determined, as is explained in more detail in the article on rank of an abelian groupRank of an abelian groupIn mathematics, the rank, Prüfer rank, or torsion-free rank of an abelian group A is the cardinality of a maximal linearly independent subset. The rank of A determines the size of the largest free abelian group contained in A. If A is torsion-free then it embeds into a vector space over the...
.
- An abelian group A is torsion-free if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it is flatFlat moduleIn Homological algebra, and algebraic geometry, a flat module over a ring R is an R-module M such that taking the tensor product over R with M preserves exact sequences. A module is faithfully flat if taking the tensor product with a sequence produces an exact sequence if and only if the original...
as a Z-moduleModule (mathematics)In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
, which means that whenever C is a subgroup of some abelian group B, then the natural map from the tensor product C ⊗ A to B ⊗ A is injective.
- Tensoring an abelian group A with Q (or any divisible groupDivisible groupIn mathematics, especially in the field of group theory, a divisible group is an abelian group in which every element can, in some sense, be divided by positive integers, or more accurately, every element is an nth multiple for each positive integer n...
) kills torsion. That is, if T is a torsion group then T ⊗ Q = 0. For a general abelian group A with torsion subgroup T one has A ⊗ Q ≅ A/T ⊗ Q.