
Generating set of a group
Encyclopedia
In abstract algebra
, a generating set of a group is a subset
that is not contained in any proper subgroup
of the group
. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination (under the group operation) of finitely many elements of the subset and their inverses
.
More generally, if S is a subset of a group G, then, the subgroup generated by S, is the smallest subgroup
of G containing every element of S, meaning the intersection over all subgroups containing the elements of S; equivalently, <S> is the subgroup of all elements of G that can be expressed as the finite product of elements in S and their inverses.
If G = <S>, then we say S generates G; and the elements in S are called generators or group generators. If S is the empty set, then is the trivial group
{e}, since we consider the empty product to be the identity.
When there is only a single element x in S, is usually written as . In this case, is the cyclic subgroup of the powers of x, a cyclic group
, and we say this group is generated by x. Equivalent to saying an element x generates a group is saying that equals the entire group G. For finite group
s, it is also equivalent to saying that
x has order
|G|.
is called finitely generated. The structure of finitely generated abelian group
s in particular is easily described. Many theorems that are true for finitely generated groups fail for groups in general. It has been proven that if a finite group is generated by a subset S, then each group element may be expressed as a word from the alphabet S of length less than or equal to the order of the group.
Every finite group is finitely generated since = G. The integer
s under addition are an example of an infinite group which is finitely generated by both 1 and −1, but the group of rationals
under addition cannot be finitely generated. No uncountable group can be finitely generated.
Different subsets of the same group can be generating subsets; for example, if p and q are integers with gcd
(p, q) = 1, then {p, q} also generates the group of integers under addition (by Bézout's identity
).
While it is true that every quotient
of a finitely generated group is finitely generated (simply take the images of the generators in the quotient), a subgroup
of a finitely generated group need not be finitely generated. For example, let G be the free group
in two generators, x and y (which is clearly finitely generated, since G = <{x,y}>), and let S be the subset consisting of all elements of G of the form ynxy−n, for n a natural number
. Since is clearly isomorphic
to the free group in countable generators, it cannot be finitely generated. However, every subgroup of a finitely generated abelian group
is in itself finitely generated. Rather more can be said about this though: the class of all finitely generated groups is closed under extensions
. To see this, take a generating set for the (finitely generated) normal subgroup
and quotient: then the generators for the normal subgroup, together with preimages of the generators for the quotient, generate the group.
by S. Every group generated by S is isomorphic to a quotient
of this group, a feature which is utilized in the expression of a group's presentation
.
.
to 9 under multiplication mod 9 (U9 = {1, 2, 4, 5, 7, 8}). All arithmetic here is done modulo
9. Seven is not a generator of U(Z9), since
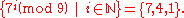
while 2 is, since:
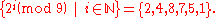
On the other hand, for n > 2 the symmetric group
of degree n is not cyclic, so it is not generated by any one element. However, it is generated by the two permutations (1 2) and (1 2 3 ... n). For example, for S3 we have:
Infinite groups can also have finite generating sets. The additive group of integers has 1 as a generating set. The element 2 is not a generating set, as the odd numbers will be missing. The two-element subset {3, 5} is a generating set, since (−5) + 3 + 3 = 1 (in fact, any pair of coprime numbers is, as a consequence of Bézout's identity
).
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a generating set of a group is a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
that is not contained in any proper subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of the group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination (under the group operation) of finitely many elements of the subset and their inverses
Inverse element
In abstract algebra, the idea of an inverse element generalises the concept of a negation, in relation to addition, and a reciprocal, in relation to multiplication. The intuition is of an element that can 'undo' the effect of combination with another given element...
.
More generally, if S is a subset of a group G, then
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of G containing every element of S, meaning the intersection over all subgroups containing the elements of S; equivalently, <S> is the subgroup of all elements of G that can be expressed as the finite product of elements in S and their inverses.
If G = <S>, then we say S generates G; and the elements in S are called generators or group generators. If S is the empty set, then
Trivial group
In mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
{e}, since we consider the empty product to be the identity.
When there is only a single element x in S,
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
, and we say this group is generated by x. Equivalent to saying an element x generates a group is saying that
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
s, it is also equivalent to saying that
x has order
Order (group theory)
In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
|G|.
Finitely generated group
If S is finite, then a group G =Finitely generated abelian group
In abstract algebra, an abelian group is called finitely generated if there exist finitely many elements x1,...,xs in G such that every x in G can be written in the formwith integers n1,...,ns...
s in particular is easily described. Many theorems that are true for finitely generated groups fail for groups in general. It has been proven that if a finite group is generated by a subset S, then each group element may be expressed as a word from the alphabet S of length less than or equal to the order of the group.
Every finite group is finitely generated since
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s under addition are an example of an infinite group which is finitely generated by both 1 and −1, but the group of rationals
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
under addition cannot be finitely generated. No uncountable group can be finitely generated.
Different subsets of the same group can be generating subsets; for example, if p and q are integers with gcd
Greatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
(p, q) = 1, then {p, q} also generates the group of integers under addition (by Bézout's identity
Bézout's identity
In number theory, Bézout's identity for two integers a, b is an expressionwhere x and y are integers , such that d is a common divisor of a and b. Bézout's lemma states that such coefficients exist for every pair of nonzero integers...
).
While it is true that every quotient
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
of a finitely generated group is finitely generated (simply take the images of the generators in the quotient), a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of a finitely generated group need not be finitely generated. For example, let G be the free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
in two generators, x and y (which is clearly finitely generated, since G = <{x,y}>), and let S be the subset consisting of all elements of G of the form ynxy−n, for n a natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
. Since
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
to the free group in countable generators, it cannot be finitely generated. However, every subgroup of a finitely generated abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
is in itself finitely generated. Rather more can be said about this though: the class of all finitely generated groups is closed under extensions
Group extension
In mathematics, a group extension is a general means of describing a group in terms of a particular normal subgroup and quotient group. If Q and N are two groups, then G is an extension of Q by N if there is a short exact sequence...
. To see this, take a generating set for the (finitely generated) normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
and quotient: then the generators for the normal subgroup, together with preimages of the generators for the quotient, generate the group.
Free group
The most general group generated by a set S is the group freely generatedFree group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
by S. Every group generated by S is isomorphic to a quotient
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
of this group, a feature which is utilized in the expression of a group's presentation
Presentation of a group
In mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
.
Frattini subgroup
An interesting companion topic is that of non-generators. An element x of the group G is a non-generator if every set S containing x that generates G, still generates G when x is removed from S. In the integers with addition, the only non-generator is 0. The set of all non-generators forms a subgroup of G, the Frattini subgroupFrattini subgroup
In mathematics, the Frattini subgroup Φ of a group G is the intersection of all maximal subgroups of G. For the case that G is the trivial group e, which has no maximal subgroups, it is defined by Φ = e...
.
Examples
The group of units U(Z9) is the group of all integers relatively primeCoprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
to 9 under multiplication mod 9 (U9 = {1, 2, 4, 5, 7, 8}). All arithmetic here is done modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
9. Seven is not a generator of U(Z9), since
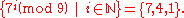
while 2 is, since:
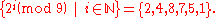
On the other hand, for n > 2 the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
of degree n is not cyclic, so it is not generated by any one element. However, it is generated by the two permutations (1 2) and (1 2 3 ... n). For example, for S3 we have:
- e = (1 2)(1 2) = (1 2) = (1 2)(1 2 3) = (1 2 3)(1 2) = (1 2 3) = (1 2)(1 2 3)(1 2)
Infinite groups can also have finite generating sets. The additive group of integers has 1 as a generating set. The element 2 is not a generating set, as the odd numbers will be missing. The two-element subset {3, 5} is a generating set, since (−5) + 3 + 3 = 1 (in fact, any pair of coprime numbers is, as a consequence of Bézout's identity
Bézout's identity
In number theory, Bézout's identity for two integers a, b is an expressionwhere x and y are integers , such that d is a common divisor of a and b. Bézout's lemma states that such coefficients exist for every pair of nonzero integers...
).
See also
- Cayley graphCayley graphIn mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
- Generating set (disambiguation) for related meanings in other structures
- Presentation of a groupPresentation of a groupIn mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...

