
Torsion-free abelian groups of rank 1
Encyclopedia
Infinitely generated abelian group
s have very complex structure and are far less well understood than finitely generated abelian groups. Even torsion-free abelian groups are vastly more varied in their characteristics than vector space
s. Torsion-free abelian groups of rank
1 are far more amenable than those of higher rank, and a satisfactory classification exists, even though there are an uncountable number of isomorphism classes.
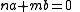
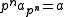
If such an element exists for every n, we say the p-root type of a is infinity, otherwise, if n is the largest non-negative integer that there is such an element, we say the p-root type of a is n .
We call the sequence of p-root types of an element a for all primes the root-type of a:
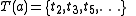 .
.
If b is another non-identity element of the group, then there is a non-trivial relation between a and b:
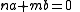
where we may take n and m to be coprime
.
As a consequence of this the root-type of b differs from the root-type of a only by a finite difference at a finite number of indices (corresponding to those primes which divide either n or m).
We call the co-finite equivalence class of a root-type to be the set of root-types that differ from it by a finite difference at a finite number of indices.
The co-finite equivalence class of the type of a non-identity element is a well-defined invariant of a torsion-free abelian group of rank 1. We call this invariant the type of a torsion-free abelian group of rank 1.
If two torsion-free abelian groups of rank 1 have the same type they may be shown to be isomorphic. Hence there is a bijection between types of torsion-free abelian groups of rank 1 and their isomorphism classes, providing a complete classification.
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s have very complex structure and are far less well understood than finitely generated abelian groups. Even torsion-free abelian groups are vastly more varied in their characteristics than vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s. Torsion-free abelian groups of rank
Rank of an abelian group
In mathematics, the rank, Prüfer rank, or torsion-free rank of an abelian group A is the cardinality of a maximal linearly independent subset. The rank of A determines the size of the largest free abelian group contained in A. If A is torsion-free then it embeds into a vector space over the...
1 are far more amenable than those of higher rank, and a satisfactory classification exists, even though there are an uncountable number of isomorphism classes.
Definition
A torsion-free abelian group of rank 1 is an abelian group such that every element except the identity has infinite order, and for any two non-identity elements a and b there is a non-trivial relation between them over the integers: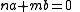
Classification of torsion-free abelian groups of rank 1
For any non-identity element a in such a group and any prime number p there may or may not be another element apn such that: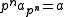
If such an element exists for every n, we say the p-root type of a is infinity, otherwise, if n is the largest non-negative integer that there is such an element, we say the p-root type of a is n .
We call the sequence of p-root types of an element a for all primes the root-type of a:
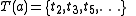 .
.If b is another non-identity element of the group, then there is a non-trivial relation between a and b:
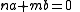
where we may take n and m to be coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
.
As a consequence of this the root-type of b differs from the root-type of a only by a finite difference at a finite number of indices (corresponding to those primes which divide either n or m).
We call the co-finite equivalence class of a root-type to be the set of root-types that differ from it by a finite difference at a finite number of indices.
The co-finite equivalence class of the type of a non-identity element is a well-defined invariant of a torsion-free abelian group of rank 1. We call this invariant the type of a torsion-free abelian group of rank 1.
If two torsion-free abelian groups of rank 1 have the same type they may be shown to be isomorphic. Hence there is a bijection between types of torsion-free abelian groups of rank 1 and their isomorphism classes, providing a complete classification.

