Integer lattice
Encyclopedia
In mathematics
, the n-dimensional integer lattice (or cubic lattice), denoted Zn, is the lattice
in the Euclidean space
Rn whose lattice points are n-tuples of integer
s. The two-dimensional integer lattice is also called the square lattice
, or grid lattice. Zn is the simplest example of a root lattice. The integer lattice is an odd unimodular lattice
.
s) of the integer lattice consists of all permutation
s and sign changes of the coordinates, and is of order 2n n! . As a matrix group
it is given by the set of all n×n signed permutation matrices. This group is isomorphic to the semidirect product
where the symmetric group
Sn acts on (Z2)n by permutation (this is a classic example of a wreath product
).
For the square lattice, this is the group of the square, or the dihedral group
of order 8; for the three dimensional cubic lattice, we get the group of the cube, or octahedral group, of order 48.
, the square lattice of points with integer coordinates is often referred to as the Diophantine plane. In mathematical terms, the Diophantine plane is the Cartesian product
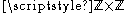of the ring of all integers 
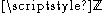. The study of Diophantine figures focuses on the selection of nodes in the Diophantine plane such that all pairwise distances are integer.
, the integer lattice is coarsely equivalent to Euclidean space
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the n-dimensional integer lattice (or cubic lattice), denoted Zn, is the lattice
Lattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
in the Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn whose lattice points are n-tuples of integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s. The two-dimensional integer lattice is also called the square lattice
Square lattice
In mathematics, the square lattice is a type of lattice in a two-dimensional Euclidean space. It is the two-dimensional version of the integer lattice. It is one of the five types of two-dimensional lattices as classified by their symmetry groups; its symmetry group is known symbolically as p4m.Two...
, or grid lattice. Zn is the simplest example of a root lattice. The integer lattice is an odd unimodular lattice
Unimodular lattice
In mathematics, a unimodular lattice is a lattice of determinant 1 or −1.The E8 lattice and the Leech lattice are two famous examples.- Definitions :...
.
Automorphism group
The automorphism group (or group of congruenceCongruence relation
In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
s) of the integer lattice consists of all permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
s and sign changes of the coordinates, and is of order 2n n
Matrix group
In mathematics, a matrix group is a group G consisting of invertible matrices over some field K, usually fixed in advance, with operations of matrix multiplication and inversion. More generally, one can consider n × n matrices over a commutative ring R...
it is given by the set of all n×n signed permutation matrices. This group is isomorphic to the semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
where the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
Sn acts on (Z2)n by permutation (this is a classic example of a wreath product
Wreath product
In mathematics, the wreath product of group theory is a specialized product of two groups, based on a semidirect product. Wreath products are an important tool in the classification of permutation groups and also provide a way of constructing interesting examples of groups.Given two groups A and H...
).
For the square lattice, this is the group of the square, or the dihedral group
Dihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
of order 8; for the three dimensional cubic lattice, we get the group of the cube, or octahedral group, of order 48.
Diophantine geometry
In the study of Diophantine geometryDiophantine geometry
In mathematics, diophantine geometry is one approach to the theory of Diophantine equations, formulating questions about such equations in terms of algebraic geometry over a ground field K that is not algebraically closed, such as the field of rational numbers or a finite field, or more general...
, the square lattice of points with integer coordinates is often referred to as the Diophantine plane. In mathematical terms, the Diophantine plane is the Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
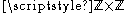of the ring of all integers 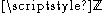. The study of Diophantine figures focuses on the selection of nodes in the Diophantine plane such that all pairwise distances are integer.Coarse geometry
In coarse geometryCoarse structure
In the mathematical fields of geometry and topology, a coarse structure on a set X is a collection of subsets of the cartesian product X × X with certain properties which allow the large-scale structure of metric spaces and topological spaces to be defined.The concern of traditional geometry and...
, the integer lattice is coarsely equivalent to Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
.