
Matrix group
Encyclopedia
In mathematics
, a matrix group is a group
G consisting of invertible matrices over some field
K, usually fixed in advance, with operations of matrix multiplication
and inversion. More generally, one can consider n × n matrices over a commutative ring
R. (The size of the matrices is restricted to be finite, as any group can be represented as a group of infinite matrices over any field.) A linear group is an abstract group that is isomorphic to a matrix group over a field K, in other words, admitting a faithful
, finite-dimensional representation
over K.
Any finite group
is linear, because it can be realized by permutation matrices using Cayley's theorem
. Among infinite groups, linear groups form an interesting and tractable class. Examples of groups that are not linear include all "sufficiently large" groups; for example, the infinite symmetric group of permutations of an infinite set.
R is itself a ring under matrix addition and multiplication. The group of units of MR(n,n) is called the general linear group
of n × n matrices over the ring R and is denoted GLn(R) or GL(n,R). All matrix groups are subgroups of some general linear group.
s. When the ring of coefficients of the matrix group is the real numbers, these groups are the classical Lie groups. When the underlying ring is a finite field the classical groups are groups of Lie type. These groups play an important role in the classification of finite simple groups
.
which states that every finite group is isomorphic to some permutation group
. Since the isomorphism property is transitive one need only consider how to form a matrix group from a permutation group.
Let G be a permutation group on n points (Ω = {1,2,…,n}) and let {g1,...,gk} be a generating set for G. The general linear group GLn(C) of n×n matrices over the complex numbers acts naturally on the vector space Cn. Let B={b1,…,bn} be the standard basis for Cn. For each gi let Mi in GLn(C) be the matrix which sends each bj to bgi(j). That is, if the permutation gi sends the point j to k then Mi sends the basis vector bj to bk. Let M be the subgroup of GLn(C) generated by {M1,…,Mk}. The action of G on Ω is then precisely the same as the action of M on B. It can be proved that the function taking each gi to Mi extends to an isomorphism and thus every group is isomorphic to a matrix group.
Note that the field (C in the above case) is irrelevant since M contains only elements with entries 0 or 1. One can just as easily perform the construction for an arbitrary field since the elements 0 and 1 exist in every field.
As an example, let G = S3, the symmetric group
on 3 points. Let g1 = (1,2,3) and g2 = (1,2). Then
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a matrix group is a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G consisting of invertible matrices over some field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K, usually fixed in advance, with operations of matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
and inversion. More generally, one can consider n × n matrices over a commutative ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
R. (The size of the matrices is restricted to be finite, as any group can be represented as a group of infinite matrices over any field.) A linear group is an abstract group that is isomorphic to a matrix group over a field K, in other words, admitting a faithful
Faithful representation
In mathematics, especially in the area of abstract algebra known as representation theory, a faithful representation ρ of a group G on a vector space V is a linear representation in which different elements g of G are represented by distinct linear mappings ρ.In more abstract language, this means...
, finite-dimensional representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
over K.
Any finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
is linear, because it can be realized by permutation matrices using Cayley's theorem
Cayley's theorem
In group theory, Cayley's theorem, named in honor of Arthur Cayley, states that every group G is isomorphic to a subgroup of the symmetric group acting on G...
. Among infinite groups, linear groups form an interesting and tractable class. Examples of groups that are not linear include all "sufficiently large" groups; for example, the infinite symmetric group of permutations of an infinite set.
Basic examples
The set MR(n,n) of n × n matrices over a commutative ringCommutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
R is itself a ring under matrix addition and multiplication. The group of units of MR(n,n) is called the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
of n × n matrices over the ring R and is denoted GLn(R) or GL(n,R). All matrix groups are subgroups of some general linear group.
Classical groups
Some particularly interesting matrix groups are the so-called classical groupClassical group
In mathematics, the classical Lie groups are four infinite families of Lie groups closely related to the symmetries of Euclidean spaces. Their finite analogues are the classical groups of Lie type...
s. When the ring of coefficients of the matrix group is the real numbers, these groups are the classical Lie groups. When the underlying ring is a finite field the classical groups are groups of Lie type. These groups play an important role in the classification of finite simple groups
Classification of finite simple groups
In mathematics, the classification of the finite simple groups is a theorem stating that every finite simple group belongs to one of four categories described below. These groups can be seen as the basic building blocks of all finite groups, in much the same way as the prime numbers are the basic...
.
Finite groups as matrix groups
Every finite group is isomorphic to some matrix group. This is similar to Cayley's theoremCayley's theorem
In group theory, Cayley's theorem, named in honor of Arthur Cayley, states that every group G is isomorphic to a subgroup of the symmetric group acting on G...
which states that every finite group is isomorphic to some permutation group
Permutation group
In mathematics, a permutation group is a group G whose elements are permutations of a given set M, and whose group operation is the composition of permutations in G ; the relationship is often written as...
. Since the isomorphism property is transitive one need only consider how to form a matrix group from a permutation group.
Let G be a permutation group on n points (Ω = {1,2,…,n}) and let {g1,...,gk} be a generating set for G. The general linear group GLn(C) of n×n matrices over the complex numbers acts naturally on the vector space Cn. Let B={b1,…,bn} be the standard basis for Cn. For each gi let Mi in GLn(C) be the matrix which sends each bj to bgi(j). That is, if the permutation gi sends the point j to k then Mi sends the basis vector bj to bk. Let M be the subgroup of GLn(C) generated by {M1,…,Mk}. The action of G on Ω is then precisely the same as the action of M on B. It can be proved that the function taking each gi to Mi extends to an isomorphism and thus every group is isomorphic to a matrix group.
Note that the field (C in the above case) is irrelevant since M contains only elements with entries 0 or 1. One can just as easily perform the construction for an arbitrary field since the elements 0 and 1 exist in every field.
As an example, let G = S3, the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
on 3 points. Let g1 = (1,2,3) and g2 = (1,2). Then
-
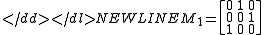
-

Notice that M1b1 = b2, M1b2 = b3 and M1b3 = b1. Likewise, M2b1 = b2, M2b2 = b1 and M2b3 = b3.
Representation theory and character theory
Linear transformations and matrices are (generally speaking) well-understood objects in mathematics and have been used extensively in the study of groups. In particular representation theoryGroup representationIn the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
studies homomorphisms from a group into a matrix group and character theoryCharacter theoryIn mathematics, more specifically in group theory, the character of a group representation is a function on the group which associates to each group element the trace of the corresponding matrix....
studies homomorphisms from a group into a field given by the trace of a representation.
Examples
- See table of Lie groupsTable of Lie groupsThis article gives a table of some common Lie groups and their associated Lie algebras.The following are noted: the topological properties of the group , as well as on their algebraic properties .For more examples of Lie groups and other...
, list of finite simple groups, and list of simple Lie groups for many examples. - See list of transitive finite linear groups.
- In 2000 a longstanding conjecture was resolved when it was shown that the braid groupBraid groupIn mathematics, the braid group on n strands, denoted by Bn, is a group which has an intuitive geometrical representation, and in a sense generalizes the symmetric group Sn. Here, n is a natural number; if n > 1, then Bn is an infinite group...
s Bn are linear for all n.
External links
- Linear groups, Encyclopaedia of Mathematics
- See table of Lie groups
-

