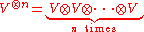Faithful representation
Encyclopedia
In mathematics
, especially in the area of abstract algebra
known as representation theory
, a faithful representation ρ of a group
G on a vector space
V is a linear representation in which different elements g of G are represented by distinct linear mappings ρ(g).
In more abstract language, this means that the group homomorphism
is injective.
Caveat: While representations of G over a field K are de facto the same as
-modules (with 
denoting the group algebra of the group G), a faithful representation of G is not necessarily a faithful module for the group algebra. In fact each faithful 
-module is a faithful representation of G, but the converse does not hold. Consider for example the natural representation of the symmetric group
Sn in n dimensions by permutation matrices, which is certainly faithful. Here the order of the group is n! while the n×n matrices form a vector space of dimension n2. As soon as n is at least 4, dimension counting means that some linear dependence must occur between permutation matrices (since 24 > 16); this relation means that the module for the group algebra is not faithful.
(the n-th tensor power of the representation V) for a sufficiently high n.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially in the area of abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
known as representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
, a faithful representation ρ of a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G on a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V is a linear representation in which different elements g of G are represented by distinct linear mappings ρ(g).
In more abstract language, this means that the group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
- ρ: G → GL(V)
is injective.
Caveat: While representations of G over a field K are de facto the same as
-modules (with denoting the group algebra of the group G), a faithful representation of G is not necessarily a faithful module for the group algebra. In fact each faithful -module is a faithful representation of G, but the converse does not hold. Consider for example the natural representation of the symmetric groupSymmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
Sn in n dimensions by permutation matrices, which is certainly faithful. Here the order of the group is n! while the n×n matrices form a vector space of dimension n2. As soon as n is at least 4, dimension counting means that some linear dependence must occur between permutation matrices (since 24 > 16); this relation means that the module for the group algebra is not faithful.
Properties
A representation V of a finite group G over an algebraically closed field K of characteristic zero is faithful (as a representation) if and only if every irreducible representation of G occurs as a subrepresentation of SnV (the n-th symmetric power of the representation V) for a sufficiently high n. Also, V is faithful (as a representation) if and only if every irreducible representation of G occurs as a subrepresentation of
(the n-th tensor power of the representation V) for a sufficiently high n.