
Polynomial basis
Encyclopedia
In mathematics
, the polynomial basis is a basis
for finite extensions of finite field
s.
Let α ∈ GF(pm) be the root of a primitive polynomial
of degree m over GF(p). The polynomial basis of GF(pm) is then

The set of elements of GF(pm) can then be represented as:
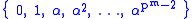
using Zech's logarithms
.
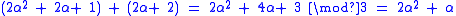
In GF(2m), addition is especially easy, since addition and subtraction modulo 2 are the same thing, and furthermore this operation can be done in hardware using the basic XOR logic gate.
Some of the methods for reducing these values include:
for the field is chosen with very few nonzero coefficients which makes squaring in polynomial basis of GF(2m) much simpler than multiplication.
applications that are based on the discrete logarithm problem such as elliptic curve cryptography
.
The advantage of the polynomial basis is that multiplication is relatively easy. For contrast, the normal basis
is an alternative to the polynomial basis and it has more complex multiplication but squaring is very simple. Hardware implementations of polynomial basis arithmetic usually consume more power than their normal basis counterparts.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the polynomial basis is a basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
for finite extensions of finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s.
Let α ∈ GF(pm) be the root of a primitive polynomial
Primitive polynomial
In field theory, a branch of mathematics, a primitive polynomial is the minimal polynomial of a primitive element of the finite extension field GF...
of degree m over GF(p). The polynomial basis of GF(pm) is then

The set of elements of GF(pm) can then be represented as:
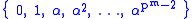
using Zech's logarithms
Zech's logarithms
Zech's logarithms are used with finite fields to reduce a high-degree polynomial that is not in the field to an element in the field...
.
Addition
Addition using the polynomial basis is as simple as addition modulo p. For example, in GF(3m):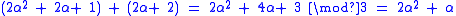
In GF(2m), addition is especially easy, since addition and subtraction modulo 2 are the same thing, and furthermore this operation can be done in hardware using the basic XOR logic gate.
Multiplication
Multiplication of two elements in the polynomial basis can be accomplished in the normal way of multiplication, but there are a number of ways to speed up multiplication, especially in hardware. Using the straightforward method to multiply two elements in GF(pm) requires up to m2 multiplications in GF(p) and up to m2 − m additions in GF(p).Some of the methods for reducing these values include:
- Lookup tables — a prestored table of results; mainly used for small fields, otherwise the table is too large to implement
- The Karatsuba-Ofman algorithm — repeatedly breaking the multiplication into pieces, decreasing the total number of multiplications but increasing the number of additions. As seen above, addition is very simple, but the overhead in breaking down and recombining the parts involved in Karatsuba-Ofman make it prohibitive for hardware, although it is often used in software. It can even be used for general multiplication, and is done in many computer algebra systemComputer algebra systemA computer algebra system is a software program that facilitates symbolic mathematics. The core functionality of a CAS is manipulation of mathematical expressions in symbolic form.-Symbolic manipulations:...
s such as Waterloo MapleWaterloo MapleWaterloo Maple Inc. is a Canadian software company, headquartered in Waterloo, Ontario. It operates under the trading name Maplesoft and is best known as the manufacturer of the Maple computer algebra system and MapleSim physical modeling and simulation software.-Corporate history:Waterloo Maple Inc...
. - Linear feedback shift registerLinear feedback shift registerA linear feedback shift register is a shift register whose input bit is a linear function of its previous state.The most commonly used linear function of single bits is XOR...
-based multiplication - Subfield computations — breaking the multiplication in GF(pm) to multiplications in GF(px) and GF(py), where x × y = m. This is not frequently used for cryptographic purposes, since some composite degree fields are avoided because of known attacks on them.
- Pipelined multipliers — storing intermediate results in buffers so that new values can be loaded into the multiplier faster
- Systolic multipliers — using many cells that communicate with neighboring cells only; typically systolic devices are used for computation-intensive operations where input and output sizes are not as important, such as multiplication.
Squaring
Squaring is an important operation because it can be used for general exponentiation as well as inversion of an element. The most basic way to square an element in the polynomial basis would be to apply a chosen multiplication algorithm on an element twice. In general case, there are minor optimizations that can be made, specifically related to the fact that when multiplying an element by itself, all the bits will be the same. In practice, however, the irreducible polynomialIrreducible polynomial
In mathematics, the adjective irreducible means that an object cannot be expressed as the product of two or more non-trivial factors in a given set. See also factorization....
for the field is chosen with very few nonzero coefficients which makes squaring in polynomial basis of GF(2m) much simpler than multiplication.
Inversion
Inversion of elements can be accomplished in many ways, including:- Lookup tables — once again, only for small fields otherwise the table is too large for implementation
- Subfield inversion — by solving systems of equations in subfields
- Repeated square and multiply — for example in GF(2m), A−1 = A2m − 2
- The Extended Euclidean algorithmExtended Euclidean algorithmThe extended Euclidean algorithm is an extension to the Euclidean algorithm. Besides finding the greatest common divisor of integers a and b, as the Euclidean algorithm does, it also finds integers x and y that satisfy Bézout's identityThe extended Euclidean algorithm is particularly useful when a...
- The Itoh-Tsujii inversion algorithmItoh-Tsujii inversion algorithmThe Itoh-Tsujii inversion algorithm is used to invert elements in a finite field. It was introduced in 1988 and first used over GF using the normal basis representation of elements, however the algorithm is generic and can be used for other bases, such as the polynomial basis. It can also be used...
Usage
The polynomial basis is frequently used in cryptographicCryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
applications that are based on the discrete logarithm problem such as elliptic curve cryptography
Elliptic curve cryptography
Elliptic curve cryptography is an approach to public-key cryptography based on the algebraic structure of elliptic curves over finite fields. The use of elliptic curves in cryptography was suggested independently by Neal Koblitz and Victor S...
.
The advantage of the polynomial basis is that multiplication is relatively easy. For contrast, the normal basis
Normal basis
In mathematics, a normal basis in field theory is a special kind of basis for Galois extensions of finite degree, characterised as forming a single orbit for the Galois group. The normal basis theorem states that any finite Galois extension of fields has a normal basis...
is an alternative to the polynomial basis and it has more complex multiplication but squaring is very simple. Hardware implementations of polynomial basis arithmetic usually consume more power than their normal basis counterparts.
See also
- normal basisNormal basisIn mathematics, a normal basis in field theory is a special kind of basis for Galois extensions of finite degree, characterised as forming a single orbit for the Galois group. The normal basis theorem states that any finite Galois extension of fields has a normal basis...
- dual basisDual basis in a field extensionIn mathematics, the linear algebra concept of dual basis can be applied in the context of a finite extension L/K, by using the field trace. This requires the property that the field trace TrL/K provides a non-degenerate quadratic form over K...
- change of bases

