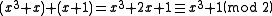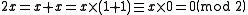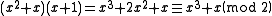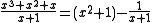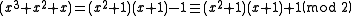Mathematics of CRC
Encyclopedia
The cyclic redundancy check
(CRC) is based on division
in the ring of polynomials
over the finite field
GF(2)
(the integers modulo 2
), that is, the set of polynomial
s where each coefficient
is either zero or one, and arithmetic operations wrap around (due to the nature of binary
arithmetic).
Any string of bits can be interpreted as the coefficients of a message polynomial of this sort, and to find the CRC, we multiply the message polynomial by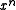
and then find the remainder when dividing by the degree
-
generator polynomial. The coefficients of the remainder polynomial are the bits of the CRC.
In general form:
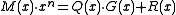
Here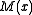
is the original message polynomial and 
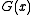is the degree-
generator polynomial. The bits of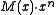 
are the original message with 
zeroes added at the end. The CRC 'checksum' is formed by the coefficients of the remainder polynomial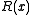 
whose degree is strictly less than 
. The quotient polynomial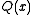 
is of no interest.
In communication, the sender attaches the
bits of R after the original message bits of M, sending out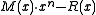 
(the codeword.) The receiver, knowing 
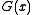and therefore 
, separates M from R and repeats the calculation, verifying that the received and computed R are equal. If they are, then the receiver assumes the received message bits are correct.
In practice CRC calculations resemble long division
in binary, except that the subtractions involved do not borrow from more significant digits, and thus become exclusive or operations.
A CRC is a checksum
in a strict mathematical sense, as it can be expressed as the weighted modulo-2 sum of per-bit syndromes, but that word is generally reserved more specifically for sums computed using larger moduli, such as 10, 256, or 65535.
CRCs can also be used as part of error-correcting codes, which allow not only the detection of transmission errors, but the reconstruction of the correct message. These codes are based on closely related mathematical principles.
Note that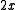
becomes zero in the above equation because addition of coefficients is performed modulo 2:
Multiplication is similar:
We can also divide polynomials mod 2 and find the quotient and remainder. For example, suppose we're dividing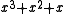
by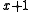 
. We would find that
In other words,
The division yields a quotient of x² + 1 with a remainder of -1, which, since it is odd, has a last bit of 1.
In the above equations,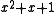
represents the original message bits 
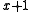is the generator polynomial, and the remainder 
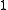(equivalently, 
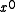) is the CRC. The degree of the generator polynomial is 1, so we first multiplied the message by 
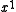to get 
.
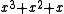and CRC presentation only affect the mapping of bit strings to the coefficients of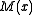
and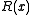 
, and do not impact the properties of the algorithm.
In practice, the last two variations are invariably used together. They change the transmitted CRC, so must be implemented at both the transmitter and the receiver. While presetting the shift register to ones is straightforward to do at both ends, inverting affects receivers implementing the first variation, because the CRC of a full codeword that already includes a CRC is no longer zero. Instead, it is a fixed non-zero pattern, the CRC of the inversion pattern of
ones.
The CRC thus may be checked either by the obvious method of computing the CRC on the message, inverting it, and comparing with the CRC in the message stream, or by calculating the CRC on the entire codeword and comparing it with an expected fixed value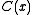
, called the check polynomial, residue or magic number
. This may be computed as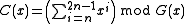
, or equivalently by computing the unmodified CRC of a message consisting of 
ones,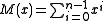 
.
These inversions are extremely common but not universally performed, even in the case of the CRC-32 or CRC-16-CCITT polynomials.
have two common hexadecimal representations. In both cases, the coefficient of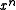 
is omitted and understood to be 1.
The msbit-first form is often referred to in the literature as the normal representation, while the lsbit-first is called the reversed representation. It is essential to use the correct form when implementing a CRC. If the coefficient of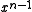
happens to be zero, the forms can be distinguished at a glance by seeing which end has the bit set.
To further confuse the matter, the paper by P. Koopman and T. Chakravarty converts CRC generator polynomials to hexadecimal numbers in yet another way: msbit-first, but including the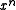
coefficient and omitting the 
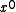coefficient. This "Koopman" representation has the advantage that the degree can be determined from the hexadecimal form and the coefficients are easy to read off in left-to-right order. However, it is not used anywhere else and is not recommended due to the risk of confusion.
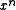through 
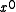coefficients of one polynomial to the 
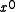through 
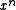coefficients of a new polynomial. That is, the reciprocal of the 
bit polynomial 
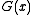is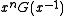 
. Example: The reverse of 
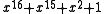is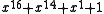 
. The most interesting property of reciprocal polynomials, when used in CRCs, is that they have exactly the same error-detecting strength as the polynomials they are reciprocals of. The reciprocal of a polynomial generates the same codewords, only bit reversed — that is, if all but the first 
bits of a codeword under the original polynomial are taken, reversed and used as a new message, the CRC of that message under the reciprocal polynomial equals the reverse of the first 
bits of the original codeword. But the reciprocal polynomial is not the same as the original polynomial, and the CRCs generated using it are not the same (even modulo bit reversal) as those generated by the original polynomial.
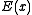is the symmetric difference of the received message codeword and the correct message codeword. An error will go undetected by a CRC algorithm if and only if the error polynomial is divisible by the CRC polynomial.
(As an aside, there is never reason to use a polynomial with a zero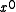
term. Recall that a CRC is the remainder of the message polynomial times x^n divided by the CRC polynomial. A polynomial with a zero 
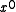term always has 
as a factor. So if 
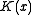is the original CRC polynomial and 
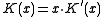, then
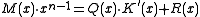
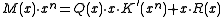
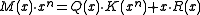
That is, the CRC of any message with the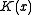
polynomial is the same as that of the same message with the 
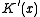polynomial with a zero appended. It is just a waste of a bit.)
The combination of these factors means that good CRC polynomials are often primitive polynomials (which have the best 2-bit error detection) or primitive polynomials of degree
, multiplied by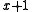 
(which detects all odd numbers of bit errors, and has half the two-bit error detection ability of a primitive polynomial of degree 
).
The results are the following:
Specific Technological References
Cyclic redundancy check
A cyclic redundancy check is an error-detecting code commonly used in digital networks and storage devices to detect accidental changes to raw data...
(CRC) is based on division
Division (mathematics)
right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
in the ring of polynomials
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
over the finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
GF(2)
GF(2)
GF is the Galois field of two elements. It is the smallest finite field.- Definition :The two elements are nearly always called 0 and 1, being the additive and multiplicative identities, respectively...
(the integers modulo 2
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
), that is, the set of polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s where each coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
is either zero or one, and arithmetic operations wrap around (due to the nature of binary
Binary numeral system
The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
arithmetic).
Any string of bits can be interpreted as the coefficients of a message polynomial of this sort, and to find the CRC, we multiply the message polynomial by
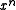and then find the remainder when dividing by the degreeDegree of a polynomial
The degree of a polynomial represents the highest degree of a polynominal's terms , should the polynomial be expressed in canonical form . The degree of an individual term is the sum of the exponents acting on the term's variables...
-
generator polynomial. The coefficients of the remainder polynomial are the bits of the CRC.In general form:
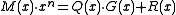
Here
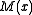is the original message polynomial and 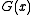is the degree- generator polynomial. The bits of 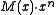are the original message with zeroes added at the end. The CRC 'checksum' is formed by the coefficients of the remainder polynomial 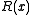whose degree is strictly less than . The quotient polynomial 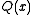is of no interest.In communication, the sender attaches the
bits of R after the original message bits of M, sending out 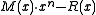(the codeword.) The receiver, knowing 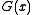and therefore , separates M from R and repeats the calculation, verifying that the received and computed R are equal. If they are, then the receiver assumes the received message bits are correct. In practice CRC calculations resemble long division
Long division
In arithmetic, long division is a standard procedure suitable for dividing simple or complex multidigit numbers. It breaks down a division problem into a series of easier steps. As in all division problems, one number, called the dividend, is divided by another, called the divisor, producing a...
in binary, except that the subtractions involved do not borrow from more significant digits, and thus become exclusive or operations.
A CRC is a checksum
Checksum
A checksum or hash sum is a fixed-size datum computed from an arbitrary block of digital data for the purpose of detecting accidental errors that may have been introduced during its transmission or storage. The integrity of the data can be checked at any later time by recomputing the checksum and...
in a strict mathematical sense, as it can be expressed as the weighted modulo-2 sum of per-bit syndromes, but that word is generally reserved more specifically for sums computed using larger moduli, such as 10, 256, or 65535.
CRCs can also be used as part of error-correcting codes, which allow not only the detection of transmission errors, but the reconstruction of the correct message. These codes are based on closely related mathematical principles.
Polynomial arithmetic modulo 2
Since the coefficients are constrained to a single bit, any math operation on CRC polynomials must map the coefficients of the result to either zero or one. For example in addition:
Note that
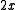becomes zero in the above equation because addition of coefficients is performed modulo 2:
Multiplication is similar:
We can also divide polynomials mod 2 and find the quotient and remainder. For example, suppose we're dividing
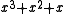by 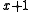. We would find that
In other words,
The division yields a quotient of x² + 1 with a remainder of -1, which, since it is odd, has a last bit of 1.
In the above equations,
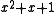represents the original message bits 111, 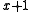is the generator polynomial, and the remainder 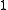(equivalently, 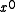) is the CRC. The degree of the generator polynomial is 1, so we first multiplied the message by 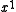to get 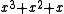.Variations
There are several standard variations on CRCs, any or all of which may be used with any CRC polynomial. Implementation variations such as endiannessEndianness
In computing, the term endian or endianness refers to the ordering of individually addressable sub-components within the representation of a larger data item as stored in external memory . Each sub-component in the representation has a unique degree of significance, like the place value of digits...
and CRC presentation only affect the mapping of bit strings to the coefficients of
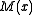and 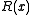, and do not impact the properties of the algorithm.
- To check the CRC, instead of calculating the CRC on the message and comparing it to the CRC, a CRC calculation may be run on the entire codeword. If the result is zero, the check passes. This works because the codeword is
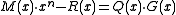, which is always divisible by 
.
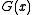- This simplifies many implementations by avoiding the need to treat the last few bytes of the message specially when checking CRCs.
- The shift register may be initialized with ones instead of zeroes. This is equivalent to inverting the first
bits of the message feeding them into the algorithm. The CRC equation becomes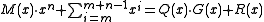 
, where 
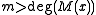is the length of the message in bits. The change this imposes on 
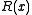is a function of the generating polynomial and the message length, 
.
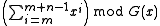- The reason this method is used is because an unmodified CRC does not distinguish between two messages which differ only in the number of leading zeroes, because leading zeroes do not affect the value of
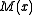. When this inversion is done, the CRC does distinguish between such messages.
- The CRC may be inverted before being appended to the message stream. While an unmodified CRC distinguishes between messages
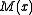with different numbers of trailing zeroes, it does not detect trailing zeroes appended after the CRC remainder itself. This is because all valid codewords are multiples of 
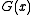, so 
times that codeword is also a multiple. (In fact, this is precisely why the first variant described above works.)
In practice, the last two variations are invariably used together. They change the transmitted CRC, so must be implemented at both the transmitter and the receiver. While presetting the shift register to ones is straightforward to do at both ends, inverting affects receivers implementing the first variation, because the CRC of a full codeword that already includes a CRC is no longer zero. Instead, it is a fixed non-zero pattern, the CRC of the inversion pattern of
ones.The CRC thus may be checked either by the obvious method of computing the CRC on the message, inverting it, and comparing with the CRC in the message stream, or by calculating the CRC on the entire codeword and comparing it with an expected fixed value
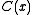, called the check polynomial, residue or magic numberMagic number (programming)
In computer programming, the term magic number has multiple meanings. It could refer to one or more of the following:* A constant numerical or text value used to identify a file format or protocol; for files, see List of file signatures...
. This may be computed as
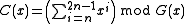, or equivalently by computing the unmodified CRC of a message consisting of ones, 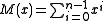.These inversions are extremely common but not universally performed, even in the case of the CRC-32 or CRC-16-CCITT polynomials.
Polynomial representations
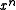All the well-known CRC generator polynomials of degree have two common hexadecimal representations. In both cases, the coefficient of is omitted and understood to be 1.- The msbit-first representation is a hexadecimal number with
bits, the least significant bit of which is always 1. The most significant bit represents the coefficient of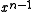 
and the least significant bit represents the coefficient of 
.
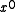- The lsbit-first representation is a hexadecimal number with
bits, the most significant bit of which is always 1. The most significant bit represents the coefficient of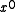 
and the least significant bit represents the coefficient of 
.
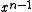The msbit-first form is often referred to in the literature as the normal representation, while the lsbit-first is called the reversed representation. It is essential to use the correct form when implementing a CRC. If the coefficient of
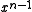happens to be zero, the forms can be distinguished at a glance by seeing which end has the bit set.To further confuse the matter, the paper by P. Koopman and T. Chakravarty converts CRC generator polynomials to hexadecimal numbers in yet another way: msbit-first, but including the
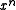coefficient and omitting the 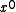coefficient. This "Koopman" representation has the advantage that the degree can be determined from the hexadecimal form and the coefficients are easy to read off in left-to-right order. However, it is not used anywhere else and is not recommended due to the risk of confusion.Reciprocal polynomials
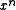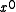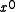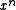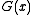A reciprocal polynomial is created by assigning the through coefficients of one polynomial to the through coefficients of a new polynomial. That is, the reciprocal of the bit polynomial is 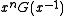. Example: The reverse of 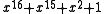is 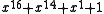. The most interesting property of reciprocal polynomials, when used in CRCs, is that they have exactly the same error-detecting strength as the polynomials they are reciprocals of. The reciprocal of a polynomial generates the same codewords, only bit reversed — that is, if all but the first bits of a codeword under the original polynomial are taken, reversed and used as a new message, the CRC of that message under the reciprocal polynomial equals the reverse of the first bits of the original codeword. But the reciprocal polynomial is not the same as the original polynomial, and the CRCs generated using it are not the same (even modulo bit reversal) as those generated by the original polynomial.Error detection strength
The error-detection ability of a CRC depends on the degree of its key polynomial and on the specific key polynomial used. The "error polynomial"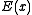 is the symmetric difference of the received message codeword and the correct message codeword. An error will go undetected by a CRC algorithm if and only if the error polynomial is divisible by the CRC polynomial.- Because a CRC is based on division, no polynomial can detect errors consisting of a string of zeroes prepended to the data, or of missing leading zeroes. However, see Variations.
- All single bit errors will be detected by any polynomial with at least two terms with non-zero coefficients. The error polynomial is
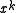, and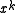 
is divisible only by polynomials 
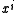where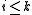 
. - All two bit errors separated by a distance less than the orderOrder (group theory)In group theory, a branch of mathematics, the term order is used in two closely related senses:* The order of a group is its cardinality, i.e., the number of its elements....
of the primitive polynomial which is a factor of the generator polynomial will be detected. The error polynomial in the two bit case is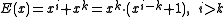
. As noted above, the 
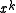term will not be divisible by the CRC polynomial, which leaves the 
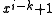term. By definition, the smallest value of 
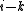such that a polynomial divides 
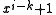is the polynomial's order or exponent. The polynomials with the largest order are called primitive polynomialPrimitive polynomialIn field theory, a branch of mathematics, a primitive polynomial is the minimal polynomial of a primitive element of the finite extension field GF...
s, and for polynomials of degree
with binary coefficients, have order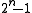 
. - All errors in an odd number of bits will be detected by a polynomial which is a multiple of
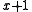. This is equivalent to the polynomial having an even number of terms with non-zero coefficients. This capacity assumes that the generator polynomial is the product of 
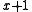and a primitive polynomial of degree 
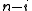since all primitive polynomials except 
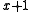have an odd number of non-zero coefficients. - All burst errorsError burstIn telecommunication, a burst error or error burst is a contiguous sequence of symbols, received over a data transmission channel, such that the first and last symbols are in error and there exists no contiguous subsequence of m correctly received symbols within the error burst.The integer...
of length
will be detected by any polynomial of degree 
or greater which has a non-zero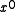 
term.
(As an aside, there is never reason to use a polynomial with a zero
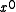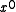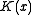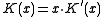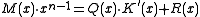
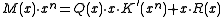
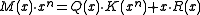
term. Recall that a CRC is the remainder of the message polynomial times x^n divided by the CRC polynomial. A polynomial with a zero term always has as a factor. So if is the original CRC polynomial and , thenThat is, the CRC of any message with the
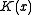polynomial is the same as that of the same message with the 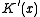polynomial with a zero appended. It is just a waste of a bit.)The combination of these factors means that good CRC polynomials are often primitive polynomials (which have the best 2-bit error detection) or primitive polynomials of degree
, multiplied by 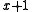(which detects all odd numbers of bit errors, and has half the two-bit error detection ability of a primitive polynomial of degree ).Bitfilters
Analysis Technique using bitfilters allows to very efficiently determine the properties of a given generator polynomial.The results are the following:
- All burst errorsError burstIn telecommunication, a burst error or error burst is a contiguous sequence of symbols, received over a data transmission channel, such that the first and last symbols are in error and there exists no contiguous subsequence of m correctly received symbols within the error burst.The integer...
(but one) with length no longer than the generator polynomial can be detected by any generator polynomial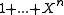
. This includes 1-bit errors (burst of length 1). The maximum length is 
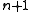, when 
is the degree of the generator polynomial (which itself has a length of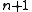 
). The exception to this result is a bit pattern the same as that of the generator polynomial. - All uneven bit errors are detected by generator polynomials with even number of terms.
- 2-Bit errors in a (multiple) distance of the longest bitfilter of even parity to a generator polynomial are not detected; all others are detected. For degrees up to 32 there is an optimal generator polynomial with that degree and even number of terms; in this case the period mentioned above is
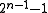. For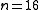 
this means that blocks of 32767 bits length do not contain undiscovered 2-Bit errors. For uneven number of terms in the generator polynomial there can be a period of 
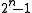; however, these generator polynomials (with odd number of terms) do not discover all odd number of errors, so they should be avoided. A list of the corresponding generators with even number of terms can be found in the link mentioned at the beginning of this section. - All single bit errors within the bitfilter period mentioned above (for even terms in the generator polynomial) can be identified uniquely by their residual. So CRC method can be used for error correction as well (within those limits, e.g. 32767 bits with optimal generator polynomials of degree 16). Since all odd errors leave an odd residual, all even an even residual, 1-bit errors and 2-bit errors can be distinguished, however not necessarily 1-bit errors and 3-bit errors. Thus bit error correction might be erroneous itself and produce more errors.
See also
General category- Error correcting code
- List of checksum algorithms
- Parity
Specific Technological References
- Adler-32Adler-32Adler-32 is a checksum algorithm which was invented by Mark Adler in 1995, and is a modification of the Fletcher checksum. Compared to a cyclic redundancy check of the same length, it trades reliability for speed. Adler-32 is more reliable than Fletcher-16, and slightly less reliable than Fletcher-32...
- Fletcher's checksumFletcher's checksumThe Fletcher checksum is an algorithm for computing a position-dependent checksum devised by John G. Fletcher at Lawrence Livermore Labs in the late 1970s. A description of the algorithm and an analysis of the performance characteristics of a particular implementation were published in the IEEE...