Algebraic normal form
Encyclopedia
In Boolean logic
, the algebraic normal form (ANF) is a method of standardizing and normalizing logical formulas. As a normal form
, it can be used in automated theorem proving
(ATP), but is more commonly used in the design of cryptographic
random number generators, specifically linear feedback shift register
s (LFSRs). A logical formula
is considered to be in ANF if and only if
it is a single algebraic sum (XOR) of a constant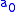
and one or more conjunction
s of the function arguments. ANF is also known as "Zhegalkin polynomial
s" and as "Positive Polarity (or Parity) Reed-Muller" expression.
Putting a formula into ANF makes it easy to identify linear
functions, as is needed for linear feedback in LFSRs: a linear function is one that is a sum of literals. Properties of nonlinear feedback shift register
s can also be deduced from certain properties of the feedback function in ANF.
The general ANF can be written as:
where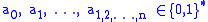
fully describes 
.
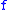For each function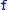
there is a unique ANF. There are only four functions with one argument: 
, 
, 
, 
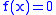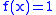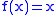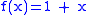(all of them are given in the ANF). To represent a function with multiple arguments one can use the following equality: 
, where 
and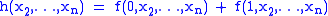 
. Indeed, if 
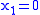then 
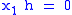and so 
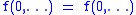; if 
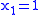then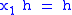 
and so 
. Since both 
and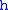 
have less arguments than 
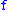it follows that using this process recursively we will finish with functions with one variable. For example, let us construct ANF of 
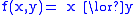(logical or): 
; since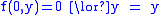 
and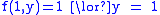 
, it follows that 
; by opening the parentheses we get the final ANF: 
.
Boolean logic
Boolean algebra is a logical calculus of truth values, developed by George Boole in the 1840s. It resembles the algebra of real numbers, but with the numeric operations of multiplication xy, addition x + y, and negation −x replaced by the respective logical operations of...
, the algebraic normal form (ANF) is a method of standardizing and normalizing logical formulas. As a normal form
Normal form
Normal form may refer to:* Normal form * Normal form * Normal form * Normal form In formal language theory:* Beta normal form* Chomsky normal form* Greibach normal form* Kuroda normal form...
, it can be used in automated theorem proving
Automated theorem proving
Automated theorem proving or automated deduction, currently the most well-developed subfield of automated reasoning , is the proving of mathematical theorems by a computer program.- Decidability of the problem :...
(ATP), but is more commonly used in the design of cryptographic
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
random number generators, specifically linear feedback shift register
Linear feedback shift register
A linear feedback shift register is a shift register whose input bit is a linear function of its previous state.The most commonly used linear function of single bits is XOR...
s (LFSRs). A logical formula
Formula
In mathematics, a formula is an entity constructed using the symbols and formation rules of a given logical language....
is considered to be in ANF if and only if
IFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
it is a single algebraic sum (XOR) of a constant
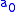and one or more conjunctionLogical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
s of the function arguments. ANF is also known as "Zhegalkin polynomial
Zhegalkin polynomial
Zhegalkin polynomials form one of many possible representations of the operations of boolean algebra. Introduced by the Russian mathematician I.I. Zhegalkin in 1927, they are the polynomials of ordinary high school algebra interpreted over the integers mod 2...
s" and as "Positive Polarity (or Parity) Reed-Muller" expression.
Putting a formula into ANF makes it easy to identify linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
functions, as is needed for linear feedback in LFSRs: a linear function is one that is a sum of literals. Properties of nonlinear feedback shift register
Shift register
In digital circuits, a shift register is a cascade of flip flops, sharing the same clock, which has the output of any one but the last flip-flop connected to the "data" input of the next one in the chain, resulting in a circuit that shifts by one position the one-dimensional "bit array" stored in...
s can also be deduced from certain properties of the feedback function in ANF.
The general ANF can be written as:
 |
 |
 |
|
 |
|
 |
|
 |
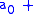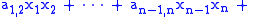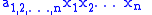where
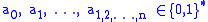fully describes 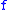.For each function
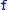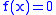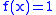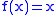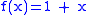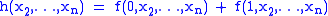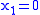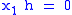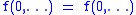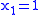there is a unique ANF. There are only four functions with one argument: , , , (all of them are given in the ANF). To represent a function with multiple arguments one can use the following equality: , where and . Indeed, if then and so ; if then 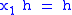and so . Since both and 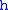have less arguments than 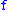it follows that using this process recursively we will finish with functions with one variable. For example, let us construct ANF of 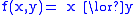(logical or): ; since 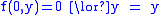and 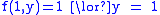, it follows that ; by opening the parentheses we get the final ANF: .See also
- Boolean function
- Conjunctive normal formConjunctive normal formIn Boolean logic, a formula is in conjunctive normal form if it is a conjunction of clauses, where a clause is a disjunction of literals.As a normal form, it is useful in automated theorem proving...
- Disjunctive normal formDisjunctive normal formIn boolean logic, a disjunctive normal form is a standardization of a logical formula which is a disjunction of conjunctive clauses. As a normal form, it is useful in automated theorem proving. A logical formula is considered to be in DNF if and only if it is a disjunction of one or more...
- Logical graphLogical graphA logical graph is a special type of diagramatic structure in any one of several systems of graphical syntax that Charles Sanders Peirce developed for logic....