Conjunctive normal form
Encyclopedia
In Boolean logic
, a formula
is in conjunctive normal form (CNF) if it is a conjunction
of clauses
, where a clause is a disjunction
of literal
s.
As a normal form, it is useful in automated theorem proving
. It is similar to the product of sums form
used in circuit theory.
All conjunctions of literals and all disjunctions of literals are in CNF, as they can be seen as conjunctions of one-literal clauses and conjunctions of a single clause, respectively. As in the disjunctive normal form
(DNF), the only propositional connectives a formula in CNF can contain are and
, or
, and not. The not operator can only be used as part of a literal, which means that it can only precede a propositional variable
.
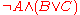
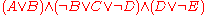
The last formula is in CNF because it can be seen as the conjunction of the two single-literal clauses
and 
. Incidentally, this formula is also in disjunctive normal form
. The following formulae are not in CNF: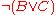
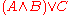
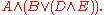
The above three formulae are respectively equivalent to the following three formulas that are in CNF:
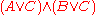
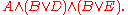
can be converted into an equivalent
formula that is in CNF. This transformation is based on rules about logical equivalence
s: the double negative law
, De Morgan's laws, and the distributive law
.
Since all logical formulae can be converted into an equivalent formula in conjunctive normal form, proofs are often based on the assumption that all formulae are CNF. However, in some cases this conversion to CNF can lead to an exponential explosion of the formula. For example, translating the following non-CNF formula into CNF produces a formula with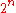
clauses:
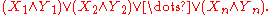
In particular, the generated formula is:
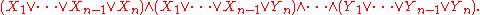
This formula contains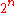
clauses; each clause contains either 
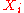or 
for each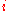 
.
There exist transformations into CNF that avoid an exponential increase in size by preserving satisfiability
rather than equivalence
. These transformations are guaranteed to only linearly increase the size of the formula, but introduce new variables. For example, the above formula can be transformed into CNF by adding variables
as follows:
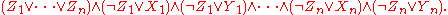
An interpretation satisfies this formula only if at least one of the new variables is true. If this variable is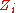
, then both 
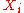and 
are true as well. This means that every model
that satisfies this formula also satisfies the original one. On the other hand, only some of the models of the original formula satisfy this one: since the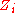
are not mentioned in the original formula, their values are irrelevant to satisfaction of it, which is not the case in the last formula. This means that the original formula and the result of the translation are equisatisfiable but not equivalent
.
An alternative translation includes also the clauses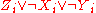
. With these clauses, the formula implies 
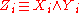; this formula is often regarded to "define" 
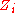to be a name for 
.
of a logical formula, which can be then used to perform first-order resolution.
involves finding assignments to the variables of a boolean formula expressed in Conjunctive Normal Form, such that the formula is true. The k-SAT problem is the problem of finding a satisfying assignment to a boolean formula expressed in CNF such that each disjunction contains at most k variables. 3-SAT
is NP-complete
(like any other k-SAT problem with k>2) while 2-SAT
is known to have solutions in polynomial time.
Typical problems in this case involve formulas in "3CNF" form: conjunctive normal form with no more than three variables per conjunct. Examples of such formulas encountered in practice can be very large, for example with 100,000 variables and 1,000,000 conjuncts.
Boolean logic
Boolean algebra is a logical calculus of truth values, developed by George Boole in the 1840s. It resembles the algebra of real numbers, but with the numeric operations of multiplication xy, addition x + y, and negation −x replaced by the respective logical operations of...
, a formula
Formula
In mathematics, a formula is an entity constructed using the symbols and formation rules of a given logical language....
is in conjunctive normal form (CNF) if it is a conjunction
Logical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
of clauses
Clause (logic)
In logic, a clause is a finite disjunction ofliterals. Clausesare usually written as follows, where the symbols l_i areliterals:l_1 \vee \cdots \vee l_nIn some cases, clauses are written as sets of literals, so that clause above...
, where a clause is a disjunction
Logical disjunction
In logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...
of literal
Literal (mathematical logic)
In mathematical logic, a literal is an atomic formula or its negation.The definition mostly appears in proof theory , e.g...
s.
As a normal form, it is useful in automated theorem proving
Automated theorem proving
Automated theorem proving or automated deduction, currently the most well-developed subfield of automated reasoning , is the proving of mathematical theorems by a computer program.- Decidability of the problem :...
. It is similar to the product of sums form
Canonical form (Boolean algebra)
In Boolean algebra, any Boolean function can be expressed in a canonical form using the dual concepts of minterms and maxterms. Minterms are called products because they are the logical AND of a set of variables, and maxterms are called sums because they are the logical OR of a set of variables In...
used in circuit theory.
All conjunctions of literals and all disjunctions of literals are in CNF, as they can be seen as conjunctions of one-literal clauses and conjunctions of a single clause, respectively. As in the disjunctive normal form
Disjunctive normal form
In boolean logic, a disjunctive normal form is a standardization of a logical formula which is a disjunction of conjunctive clauses. As a normal form, it is useful in automated theorem proving. A logical formula is considered to be in DNF if and only if it is a disjunction of one or more...
(DNF), the only propositional connectives a formula in CNF can contain are and
Logical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
, or
Logical disjunction
In logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...
, and not. The not operator can only be used as part of a literal, which means that it can only precede a propositional variable
Propositional variable
In mathematical logic, a propositional variable is a variable which can either be true or false...
.
Examples and counterexamples
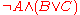
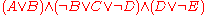
All of the following formulas are in CNF:The last formula is in CNF because it can be seen as the conjunction of the two single-literal clauses
and . Incidentally, this formula is also in disjunctive normal formDisjunctive normal form
In boolean logic, a disjunctive normal form is a standardization of a logical formula which is a disjunction of conjunctive clauses. As a normal form, it is useful in automated theorem proving. A logical formula is considered to be in DNF if and only if it is a disjunction of one or more...
. The following formulae are not in CNF:
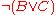
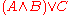
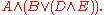
The above three formulae are respectively equivalent to the following three formulas that are in CNF:
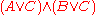
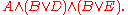
Conversion into CNF
Every propositional formulaPropositional formula
In propositional logic, a propositional formula is a type of syntactic formula which is well formed and has a truth value. If the values of all variables in a propositional formula are given, it determines a unique truth value...
can be converted into an equivalent
Logical equivalence
In logic, statements p and q are logically equivalent if they have the same logical content.Syntactically, p and q are equivalent if each can be proved from the other...
formula that is in CNF. This transformation is based on rules about logical equivalence
Logical equivalence
In logic, statements p and q are logically equivalent if they have the same logical content.Syntactically, p and q are equivalent if each can be proved from the other...
s: the double negative law
Double negative elimination
In propositional logic, the inference rules double negative elimination allow deriving the double negative equivalent by adding or removing a pair of negation signs...
, De Morgan's laws, and the distributive law
Distributivity
In mathematics, and in particular in abstract algebra, distributivity is a property of binary operations that generalizes the distributive law from elementary algebra.For example:...
.
Since all logical formulae can be converted into an equivalent formula in conjunctive normal form, proofs are often based on the assumption that all formulae are CNF. However, in some cases this conversion to CNF can lead to an exponential explosion of the formula. For example, translating the following non-CNF formula into CNF produces a formula with
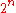clauses: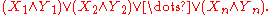In particular, the generated formula is:
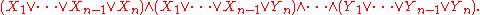
This formula contains
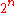clauses; each clause contains either 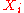or for each 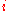.There exist transformations into CNF that avoid an exponential increase in size by preserving satisfiability
Boolean satisfiability problem
In computer science, satisfiability is the problem of determining if the variables of a given Boolean formula can be assigned in such a way as to make the formula evaluate to TRUE...
rather than equivalence
Logical equivalence
In logic, statements p and q are logically equivalent if they have the same logical content.Syntactically, p and q are equivalent if each can be proved from the other...
. These transformations are guaranteed to only linearly increase the size of the formula, but introduce new variables. For example, the above formula can be transformed into CNF by adding variables
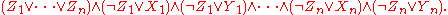
as follows:An interpretation satisfies this formula only if at least one of the new variables is true. If this variable is
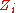, then both 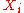and are true as well. This means that every modelModel theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
that satisfies this formula also satisfies the original one. On the other hand, only some of the models of the original formula satisfy this one: since the
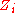are not mentioned in the original formula, their values are irrelevant to satisfaction of it, which is not the case in the last formula. This means that the original formula and the result of the translation are equisatisfiable but not equivalentLogical equivalence
In logic, statements p and q are logically equivalent if they have the same logical content.Syntactically, p and q are equivalent if each can be proved from the other...
.
An alternative translation includes also the clauses
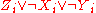. With these clauses, the formula implies 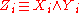; this formula is often regarded to "define" 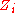to be a name for .First-order logic
In first order logic, conjunctive normal form can be taken further to yield the clausal normal formClausal normal form
The clausal normal form of a logical formula is used in logic programming and many theorem proving systems. A formula in clause normal form is a set of clauses, interpreted as a conjunction...
of a logical formula, which can be then used to perform first-order resolution.
Computational complexity
An important set of problems in computational complexityComputational Complexity
Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...
involves finding assignments to the variables of a boolean formula expressed in Conjunctive Normal Form, such that the formula is true. The k-SAT problem is the problem of finding a satisfying assignment to a boolean formula expressed in CNF such that each disjunction contains at most k variables. 3-SAT
Boolean satisfiability problem
In computer science, satisfiability is the problem of determining if the variables of a given Boolean formula can be assigned in such a way as to make the formula evaluate to TRUE...
is NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
(like any other k-SAT problem with k>2) while 2-SAT
2-satisfiability
In computer science, 2-satisfiability is the problem of determining whether a collection of two-valued variables with constraints on pairs of variables can be assigned values satisfying all the constraints...
is known to have solutions in polynomial time.
Typical problems in this case involve formulas in "3CNF" form: conjunctive normal form with no more than three variables per conjunct. Examples of such formulas encountered in practice can be very large, for example with 100,000 variables and 1,000,000 conjuncts.
Converting from first-order logic
To convert first-order logic to CNF:- Convert to negation normal form.
- Eliminate implications: convert
to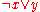 
- Move NOTs inwards by repeatedly applying DeMorgan's Law. Specifically, replace
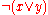with 
; replace 
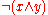with 
; and replace 
with 
.
- Eliminate implications: convert
- Standardize variables
- For sentences like (∀x P(x)) ∨ (∃x Q(x)) which use the same variable name twice, change the name of one of the variables. This avoids confusion later when we drop the quantifiers.
- From ∀x [∃y Animal(y) ∧ ¬Loves(x, y)] ∨ [∃y Loves(y, x)]. we obtain: ∀x [∃y Animal(y) ∧ ¬Loves(x, y)] ∨ [∃z Loves(z,x)].
- Skolemize the statement
- ∃x P(x) into P(A), where A is a new constant (consult linked article for more details)
- Drop universal quantifiers
- Distribute ORs over ANDs.
See also
- Algebraic normal formAlgebraic normal formIn Boolean logic, the algebraic normal form is a method of standardizing and normalizing logical formulas. As a normal form, it can be used in automated theorem proving , but is more commonly used in the design of cryptographic random number generators, specifically linear feedback shift registers...
- Disjunctive normal formDisjunctive normal formIn boolean logic, a disjunctive normal form is a standardization of a logical formula which is a disjunction of conjunctive clauses. As a normal form, it is useful in automated theorem proving. A logical formula is considered to be in DNF if and only if it is a disjunction of one or more...
- Horn clauseHorn clauseIn mathematical logic, a Horn clause is a clause with at most one positive literal. They are named after the logician Alfred Horn, who first pointed out the significance of such clauses in 1951...
- Quine–McCluskey algorithm