
Horn clause
Encyclopedia
In mathematical logic
, a Horn clause is a clause
(a disjunction of literal
s) with at most one positive literal. They are named after the logician Alfred Horn
, who first pointed out the significance of such clauses in 1951. Horn clauses play a basic role in logic programming
and are important for constructive logic.
A Horn clause with exactly one positive literal is a definite clause; in universal algebra
definite clauses appear as quasiidentities
. The positive literal is called the head and the negative literals form the body of the clause. A Horn clause containing only negative literals is sometimes called a goal clause or query clause, especially in logic programming
. A dual-Horn clause is a clause with at most one negative literal. A definite clause with no negative literals simply asserts a given propostion sometimes called a fact. A Horn formula is a string of existential or universal quantifiers followed by a conjunction of Horn clauses; that is, a prenex normal form
formula whose matrix is in conjunctive normal form
with all Horn clauses.
The following is an example of a (definite) Horn clause:
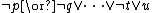
Such a formula can also be written equivalently in the form of an implication:
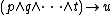
Horn clauses can be propositional or first order
, depending on whether we consider propositional or first-order literals.
Horn (1951) has shown that validity of Horn formulas is preserved under nonempty direct product
s, and conjectured that the converse also holds. This was disproved by Chang and Morel (1958), however Keisler (1965) proved that a formula is Horn if and only if it is preserved under nonempty reduced product
s.
Horn clauses are relevant to theorem proving by first-order resolution, in that the resolution of two Horn clauses is itself a Horn clause. Moreover, the resolution of a goal clause and a definite clause is again a goal clause. In automated theorem proving
, this can lead to greater efficiencies in proving a theorem represented as a goal clause.
Horn clause logic is equivalent in computational power to a universal Turing machine
. In fact, the resolution of a goal clause with a definite clause to produce a new goal clause is the basis of the SLD resolution
inference rule, used to implement logic programming
and the programming language Prolog
. In logic programming a definite clause behaves as a goal-reduction procedure. For example, the Horn clause written above behaves as the procedure:
To emphasize this backwards use of the clause, it is often written using the consequence operator:
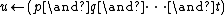
This is written in Prolog
as follows:
u :- p, q, ..., t.
Propositional Horn clauses are also of interest in computational complexity
, where the problem of finding a set of variable assignments to make a conjunction of Horn clauses true is a P-complete
problem (in fact solvable in linear time), sometimes called HORNSAT
. (The unrestricted Boolean satisfiability problem
is an NP-complete
problem however.) Satisfiability of first-order Horn clauses is undecidable
.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, a Horn clause is a clause
Clause (logic)
In logic, a clause is a finite disjunction ofliterals. Clausesare usually written as follows, where the symbols l_i areliterals:l_1 \vee \cdots \vee l_nIn some cases, clauses are written as sets of literals, so that clause above...
(a disjunction of literal
Literal (mathematical logic)
In mathematical logic, a literal is an atomic formula or its negation.The definition mostly appears in proof theory , e.g...
s) with at most one positive literal. They are named after the logician Alfred Horn
Alfred Horn
Alfred Horn was an American mathematician notable for his work in lattice theory and universal algebra. His 1951 paper "On sentences which are true of direct unions of algebras" described Horn clauses and Horn sentences, which later would form the foundation of logic programming.Horn was born on...
, who first pointed out the significance of such clauses in 1951. Horn clauses play a basic role in logic programming
Logic programming
Logic programming is, in its broadest sense, the use of mathematical logic for computer programming. In this view of logic programming, which can be traced at least as far back as John McCarthy's [1958] advice-taker proposal, logic is used as a purely declarative representation language, and a...
and are important for constructive logic.
A Horn clause with exactly one positive literal is a definite clause; in universal algebra
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
definite clauses appear as quasiidentities
Quasiidentity
In universal algebra, a quasiidentity is an implication of the formwhere s1, ..., sn, s and t1, ..., tn,t are terms built up from variables using the operation symbols of the specified signature....
. The positive literal is called the head and the negative literals form the body of the clause. A Horn clause containing only negative literals is sometimes called a goal clause or query clause, especially in logic programming
Logic programming
Logic programming is, in its broadest sense, the use of mathematical logic for computer programming. In this view of logic programming, which can be traced at least as far back as John McCarthy's [1958] advice-taker proposal, logic is used as a purely declarative representation language, and a...
. A dual-Horn clause is a clause with at most one negative literal. A definite clause with no negative literals simply asserts a given propostion sometimes called a fact. A Horn formula is a string of existential or universal quantifiers followed by a conjunction of Horn clauses; that is, a prenex normal form
Prenex normal form
A formula of the predicate calculus is in prenex normal form if it is written as a string of quantifiers followed by a quantifier-free part .Every formula in classical logic is equivalent to a formula in prenex normal form...
formula whose matrix is in conjunctive normal form
Conjunctive normal form
In Boolean logic, a formula is in conjunctive normal form if it is a conjunction of clauses, where a clause is a disjunction of literals.As a normal form, it is useful in automated theorem proving...
with all Horn clauses.
The following is an example of a (definite) Horn clause:
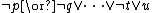
Such a formula can also be written equivalently in the form of an implication:
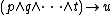
Horn clauses can be propositional or first order
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
, depending on whether we consider propositional or first-order literals.
Horn (1951) has shown that validity of Horn formulas is preserved under nonempty direct product
Direct product
In mathematics, one can often define a direct product of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets, together with a suitably defined structure on the product set....
s, and conjectured that the converse also holds. This was disproved by Chang and Morel (1958), however Keisler (1965) proved that a formula is Horn if and only if it is preserved under nonempty reduced product
Reduced product
In model theory, a branch of mathematical logic, and in algebra, the reduced product is a construction that generalizes both direct product and ultraproduct....
s.
Horn clauses are relevant to theorem proving by first-order resolution, in that the resolution of two Horn clauses is itself a Horn clause. Moreover, the resolution of a goal clause and a definite clause is again a goal clause. In automated theorem proving
Automated theorem proving
Automated theorem proving or automated deduction, currently the most well-developed subfield of automated reasoning , is the proving of mathematical theorems by a computer program.- Decidability of the problem :...
, this can lead to greater efficiencies in proving a theorem represented as a goal clause.
Horn clause logic is equivalent in computational power to a universal Turing machine
Universal Turing machine
In computer science, a universal Turing machine is a Turing machine that can simulate an arbitrary Turing machine on arbitrary input. The universal machine essentially achieves this by reading both the description of the machine to be simulated as well as the input thereof from its own tape. Alan...
. In fact, the resolution of a goal clause with a definite clause to produce a new goal clause is the basis of the SLD resolution
SLD resolution
SLD resolution is the basic inference rule used in logic programming. It is a refinement of resolution, which is both sound and refutation complete for Horn clauses.-The SLD inference rule:...
inference rule, used to implement logic programming
Logic programming
Logic programming is, in its broadest sense, the use of mathematical logic for computer programming. In this view of logic programming, which can be traced at least as far back as John McCarthy's [1958] advice-taker proposal, logic is used as a purely declarative representation language, and a...
and the programming language Prolog
Prolog
Prolog is a general purpose logic programming language associated with artificial intelligence and computational linguistics.Prolog has its roots in first-order logic, a formal logic, and unlike many other programming languages, Prolog is declarative: the program logic is expressed in terms of...
. In logic programming a definite clause behaves as a goal-reduction procedure. For example, the Horn clause written above behaves as the procedure:
- to show
 , show
, show  and show
and show 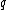 and
and  and show
and show  .
.
To emphasize this backwards use of the clause, it is often written using the consequence operator:
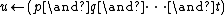
This is written in Prolog
Prolog
Prolog is a general purpose logic programming language associated with artificial intelligence and computational linguistics.Prolog has its roots in first-order logic, a formal logic, and unlike many other programming languages, Prolog is declarative: the program logic is expressed in terms of...
as follows:
u :- p, q, ..., t.
Propositional Horn clauses are also of interest in computational complexity
Computational Complexity
Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...
, where the problem of finding a set of variable assignments to make a conjunction of Horn clauses true is a P-complete
P-complete
In complexity theory, the notion of P-complete decision problems is useful in the analysis of both:# which problems are difficult to parallelize effectively, and;# which problems are difficult to solve in limited space....
problem (in fact solvable in linear time), sometimes called HORNSAT
Horn-satisfiability
In formal logic, Horn-satisfiability, or HORNSAT, is the problem of deciding whether a given set of propositional Horn clauses is satisfiable....
. (The unrestricted Boolean satisfiability problem
Boolean satisfiability problem
In computer science, satisfiability is the problem of determining if the variables of a given Boolean formula can be assigned in such a way as to make the formula evaluate to TRUE...
is an NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
problem however.) Satisfiability of first-order Horn clauses is undecidable
Undecidable
Undecidable may refer to:In mathematics and logic* Undecidable problem - a decision problem which no algorithm can decide* "Undecidable" is sometimes used as a synonym of "independent", where a formula in mathematical logic is independent of a logical theory if neither that formula nor its negation...
.

