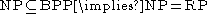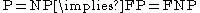Boolean satisfiability problem
Encyclopedia
In computer science
, satisfiability (often written in all capitals or abbreviated SAT) is the problem of determining if the variables of a given Boolean
formula can be assigned in such a way as to make the formula evaluate to TRUE. Equally important is to determine whether no such assignments exist, which would imply that the function expressed by the formula is identically FALSE for all possible variable assignments. In this latter case, we would say that the function is unsatisfiable; otherwise it is satisfiable. For example, the formula a AND b is satisfiable because one can find the values a = TRUE and b = TRUE, which make a AND b TRUE. To emphasize the binary nature of this problem, it is frequently referred to as Boolean or propositional satisfiability.
SAT was the first known example of an NP-complete
problem. That briefly means that there is no known algorithm that efficiently solves all instances of SAT, and it is generally believed (but not proven, see P versus NP problem) that no such algorithm can exist. Further, a wide range of other naturally occurring decision and optimization problems can be transformed into instances of SAT. A class of algorithms called SAT solvers can efficiently solve a large enough subset of SAT instances to be useful in various practical areas such as circuit design
and automatic theorem proving, by solving SAT instances made by transforming problems that arise in those areas. Extending the capabilities of SAT solving algorithms is an ongoing area of progress. However, no current such methods can efficiently solve all SAT instances.
, the satisfiability problem (SAT) is a decision problem
, whose instance is a Boolean expression written using only AND, OR, NOT, variables, and parentheses. The question is: given the expression, is there some assignment of TRUE and FALSE values to the variables that will make the entire expression true? A formula of propositional logic is said to be satisfiable if logical value
s can be assigned to its variables
in a way that makes the formula true. The Boolean satisfiability problem is NP-complete
. The propositional satisfiability problem (PSAT), which decides whether a given propositional formula
is satisfiable, is of central importance in various areas of computer science
, including theoretical computer science
, algorithmics, artificial intelligence
, hardware design, electronic design automation
, and verification.
A literal is either a variable or the negation of a variable (the negation of an expression can be reduced to negated variables by De Morgan's laws). For example,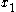
is a positive literal and 
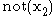is a negative literal.
A clause is a disjunction of literals. For example,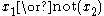
is a clause (read as "x-sub-one or not x-sub-2").
There are several special cases of the Boolean satisfiability problem in which the formulae are required to be conjunctions
of clauses (i.e. formulae in conjunctive normal form
). Determining the satisfiability of a formula in conjunctive normal form where each clause is limited to at most three literals is NP-complete; this problem is called "3SAT", "3CNFSAT", or "3-satisfiability". Determining the satisfiability of a formula in which each clause is limited to at most two literals is NL-complete
; this problem is called "2SAT". Determining the satisfiability of a formula in which each clause is a Horn clause
(i.e. it contains at most one positive literal) is P-complete
; this problem is called Horn-satisfiability
.
The Cook–Levin theorem states that the Boolean satisfiability problem is NP-complete, and in fact, this was the first decision problem proved to be NP-complete. However, beyond this theoretical significance, efficient and scalable algorithms for SAT that were developed over the last decade have contributed to dramatic advances in our ability to automatically solve problem instances involving tens of thousands of variables and millions of constraints. Examples of such problems in electronic design automation (EDA) include formal equivalence checking
, model checking
, formal verification
of pipelined microprocessors
, automatic test pattern generation
, routing of FPGAs, and so on. A SAT-solving engine is now considered to be an essential component in the EDA toolbox.
problem, as proved by Stephen Cook
in 1971 (see Cook's theorem for the proof). Until that time, the concept of an NP-complete problem did not even exist. The problem remains NP-complete even if all expressions are written in conjunctive normal form
with 3 variables per clause (3-CNF), yielding the 3SAT problem. This means the expression has the form: AND AND AND ...
where each x is a variable or a negation of a variable, and each variable can appear multiple times in the expression.
A useful property of Cook's reduction is that it preserves the number of accepting answers. For example, if a graph has 17 valid 3-colorings, the SAT formula produced by the reduction will have 17 satisfying assignments.
NP-completeness only refers to the run-time of the worst case instances. Many of the instances that occur in practical applications can be solved much more quickly. See runtime behavior below.
SAT is easier if the formulas are restricted to those in disjunctive normal form
, that is, they are disjunction (OR) of terms, where each term is a conjunction (AND) of literals (possibly negated variables). Such a formula is indeed satisfiable if and only if at least one of its terms is satisfiable, and a term is satisfiable if and only if it does not contain both x and NOT x for some variable x. This can be checked in polynomial time.
. Similarly, if we limit the number of literals per clause to 2 and change the AND operations to XOR operations, the result is exclusive-or 2-satisfiability, a problem complete for SL
= L
.
One of the most important restrictions of SAT is HORNSAT, where the formula is a conjunction of Horn clause
s. This problem is solved by the polynomial-time Horn-satisfiability
algorithm, and is in fact P-complete
. It can be seen as P's
version of the Boolean satisfiability problem.
Provided that the complexity classes P and NP are not equal, none of these restrictions are NP-complete, unlike SAT. The assumption that P and NP are not equal is currently not proven.
.
Here is an example, where ¬ indicates negation
:
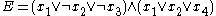
E has two clauses (denoted by parentheses), four variables (x1, x2, x3, x4), and k=3 (three literals per clause).
To solve this instance of the decision problem we must determine whether there is a truth value (TRUE or FALSE) we can assign to each of the variables (x1 through x4) such that the entire expression is TRUE. In this instance, there is such an assignment (x1 = TRUE, x2 = TRUE, x3=TRUE, x4=TRUE), so the answer to this instance is YES. This is one of many possible assignments, with for instance, any set of assignments including x1 = TRUE being sufficient. If there were no such assignment(s), the answer would be NO.
3-SAT is NP-complete
and it is used as a starting point for proving that other problems are also NP-hard
. This is done by polynomial-time reduction
from 3-SAT to the other problem. An example of a problem where this method has been used is the Clique problem
. 3-SAT can be further restricted to One-in-three 3SAT
, where we ask if exactly one of the literals in each clause is true, rather than at least one. This restriction remains NP-complete.
There is a simple randomized algorithm due to that runs in time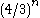
where n is the number of clauses and succeeds with high probability to correctly decide 3-Sat.
The exponential time hypothesis
is that no algorithm can solve 3-Sat in time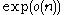
.
of one variable from a set of other variables. Indeed, one such clause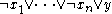
can be rewritten as 
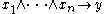, that is, if 
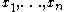are all true, then y needs to be true as well.
The problem of deciding whether a set of Horn clauses is satisfiable is in P. This problem can indeed be solved by a single step of the Unit propagation
, which produces the single minimal (w.r.t. the set of literal assigned to true) model of the set of Horn clauses.
A generalization of the class of Horn formulae is that of renamable-Horn formulae, which is the set of formulae that can be placed in Horn form by replacing some variables with their respective negation. Checking the existence of such a replacement can be done in linear time; therefore, the satisfiability of such formulae is in P as it can be solved by first performing this replacement and then checking the satisfiability of the resulting Horn formula.
), the clauses can be viewed as a system of linear equations and corresponding methods such as Gaussian elimination
can be used to find the solution.
Schaefer's dichotomy theorem states that, for any restriction to Boolean operators that can be used to form these subformulae, the corresponding satisfiability problem is in P or NP-complete. The membership in P of the satisfiability of 2CNF and Horn formulae are special cases of this theorem.
(SMT) that can enrich CNF formulas with linear constraints, arrays, all-different constraints, uninterpreted function
s, etc. Such extensions typically remain NP-complete, but very efficient solvers are now available that can handle many such kinds of constraints.
The satisfiability problem becomes more difficult (PSPACE-complete) if we extend our logic to include second-order Booleans, allowing quantifiers such as "for all" and "there exists" that bind the Boolean variables. An example of such an expression would be:
SAT itself uses only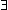
quantifiers. If we allow only 
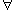quantifiers, it becomes the Co-NP-complete
tautology
problem. If we allow both, the problem is called the quantified Boolean formula problem (QBF), which can be shown to be PSPACE-complete
. It is widely believed that PSPACE-complete problems are strictly harder than any problem in NP, although this has not yet been proved.
A number of variants deal with the number of variable assignments making the formula true. Ordinary SAT asks if there is at least one such assignment. MAJSAT, which asks if the majority of all assignments make the formula true, is complete for PP
, a probabilistic class. The problem of how many variable assignments satisfy a formula, not a decision problem, is in #P
. UNIQUE-SAT or USAT or Unambiguous SAT is the problem of determining whether a formula known to have either zero or one satisfying assignments has zero or has one. Although this problem seems easier, it has been shown
that if there is a practical (randomized polynomial-time) algorithm to solve this problem, then all problems in NP can be solved just as easily.
The maximum satisfiability problem
, an FNP
generalization of SAT, asks for the maximum number of clauses which can be satisfied by any assignment. It has efficient approximation algorithm
s, but is NP-hard to solve exactly. Worse still, it is APX
-complete, meaning there is no polynomial-time approximation scheme
(PTAS) for this problem unless P=NP.
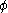. If the answer is "no", the formula is unsatisfable. Otherwise, the question is asked on 
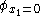, i.e. the first variable is assumed to be 0. If the answer is "no", it is assumed that 
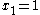, otherwise 
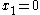. Values of other variables are found subsequently.
This property is used in several theorems in complexity theory:
(well known implementation include Chaff
, GRASP
) and stochastic local search
algorithms, such as WalkSAT
.
A DPLL SAT solver employs a systematic backtracking search procedure to explore the (exponentially sized) space of variable assignments looking for satisfying assignments. The basic search procedure was proposed in two seminal papers in the early 60s (see references below) and is now commonly referred to as the Davis–Putnam–Logemann–Loveland algorithm (“DPLL” or “DLL”). Theoretically, exponential lower bounds have been proved for the DPLL family of algorithms.
Modern SAT solvers (developed in the last ten years) come in two flavors: "conflict-driven" and "look-ahead". Conflict-driven solvers augment the basic DPLL search algorithm with efficient conflict analysis, clause learning, non-chronological backtracking (aka backjumping
), as well as "two-watched-literals" unit propagation, adaptive branching, and random restarts. These "extras" to the basic systematic search have been empirically shown to be essential for handling the large SAT instances that arise in electronic design automation
(EDA). Look-ahead solvers have especially strengthened reductions (going beyond unit-clause propagation) and the heuristics, and they are generally stronger than conflict-driven solvers on hard instances (while conflict-driven solvers can be much better on large instances which actually have an easy instance inside).
Modern SAT solvers are also having significant impact on the fields of software verification, constraint solving in artificial intelligence, and operations research, among others. Powerful solvers are readily available as free and open source software
. In particular, the conflict-driven MiniSAT, which was relatively successful at the 2005 SAT competition, only has about 600 lines of code. An example for look-ahead solvers is march_dl, which won a prize at the 2007 SAT competition.
Certain types of large random satisfiable instances of SAT can be solved by survey propagation (SP). Particularly in hardware design and verification applications, satisfiability and other logical properties of a given propositional formula are sometimes decided based on a representation of the formula as a binary decision diagram
(BDD).
Propositional satisfiability has various generalisations, including satisfiability for quantified Boolean formula problem, for first- and second-order logic
, constraint satisfaction problem
s, 0-1 integer programming, and maximum satisfiability problem
.
Many other decision problems, such as graph coloring
problems, planning problems
, and scheduling problems, can be easily encoded into SAT.
SAT Applications:
SAT Solvers:
International Conference on Theory and Applications of Satisfiability Testing:
Publications:
Benchmarks:
SAT solving in general:
Evaluation of SAT solvers:
----
This article includes material from a column in the ACM SIGDA e-newsletter by Prof. Karem Sakallah
Original text is available here
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, satisfiability (often written in all capitals or abbreviated SAT) is the problem of determining if the variables of a given Boolean
Boolean logic
Boolean algebra is a logical calculus of truth values, developed by George Boole in the 1840s. It resembles the algebra of real numbers, but with the numeric operations of multiplication xy, addition x + y, and negation −x replaced by the respective logical operations of...
formula can be assigned in such a way as to make the formula evaluate to TRUE. Equally important is to determine whether no such assignments exist, which would imply that the function expressed by the formula is identically FALSE for all possible variable assignments. In this latter case, we would say that the function is unsatisfiable; otherwise it is satisfiable. For example, the formula a AND b is satisfiable because one can find the values a = TRUE and b = TRUE, which make a AND b TRUE. To emphasize the binary nature of this problem, it is frequently referred to as Boolean or propositional satisfiability.
SAT was the first known example of an NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
problem. That briefly means that there is no known algorithm that efficiently solves all instances of SAT, and it is generally believed (but not proven, see P versus NP problem) that no such algorithm can exist. Further, a wide range of other naturally occurring decision and optimization problems can be transformed into instances of SAT. A class of algorithms called SAT solvers can efficiently solve a large enough subset of SAT instances to be useful in various practical areas such as circuit design
Circuit design
The process of circuit design can cover systems ranging from complex electronic systems all the way down to the individual transistors within an integrated circuit...
and automatic theorem proving, by solving SAT instances made by transforming problems that arise in those areas. Extending the capabilities of SAT solving algorithms is an ongoing area of progress. However, no current such methods can efficiently solve all SAT instances.
Basic definitions, terminology and applications
In complexity theoryComputational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, the satisfiability problem (SAT) is a decision problem
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
, whose instance is a Boolean expression written using only AND, OR, NOT, variables, and parentheses. The question is: given the expression, is there some assignment of TRUE and FALSE values to the variables that will make the entire expression true? A formula of propositional logic is said to be satisfiable if logical value
Logical value
In logic and mathematics, a truth value, sometimes called a logical value, is a value indicating the relation of a proposition to truth.In classical logic, with its intended semantics, the truth values are true and false; that is, classical logic is a two-valued logic...
s can be assigned to its variables
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
in a way that makes the formula true. The Boolean satisfiability problem is NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
. The propositional satisfiability problem (PSAT), which decides whether a given propositional formula
Propositional formula
In propositional logic, a propositional formula is a type of syntactic formula which is well formed and has a truth value. If the values of all variables in a propositional formula are given, it determines a unique truth value...
is satisfiable, is of central importance in various areas of computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, including theoretical computer science
Theoretical computer science
Theoretical computer science is a division or subset of general computer science and mathematics which focuses on more abstract or mathematical aspects of computing....
, algorithmics, artificial intelligence
Artificial intelligence
Artificial intelligence is the intelligence of machines and the branch of computer science that aims to create it. AI textbooks define the field as "the study and design of intelligent agents" where an intelligent agent is a system that perceives its environment and takes actions that maximize its...
, hardware design, electronic design automation
Electronic design automation
Electronic design automation is a category of software tools for designing electronic systems such as printed circuit boards and integrated circuits...
, and verification.
A literal is either a variable or the negation of a variable (the negation of an expression can be reduced to negated variables by De Morgan's laws). For example,
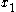is a positive literal and 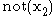is a negative literal.A clause is a disjunction of literals. For example,
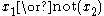is a clause (read as "x-sub-one or not x-sub-2").There are several special cases of the Boolean satisfiability problem in which the formulae are required to be conjunctions
Logical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
of clauses (i.e. formulae in conjunctive normal form
Conjunctive normal form
In Boolean logic, a formula is in conjunctive normal form if it is a conjunction of clauses, where a clause is a disjunction of literals.As a normal form, it is useful in automated theorem proving...
). Determining the satisfiability of a formula in conjunctive normal form where each clause is limited to at most three literals is NP-complete; this problem is called "3SAT", "3CNFSAT", or "3-satisfiability". Determining the satisfiability of a formula in which each clause is limited to at most two literals is NL-complete
NL-complete
In computational complexity theory, NL-Complete is a complexity class which is complete for NL. It contains the most "difficult" or "expressive" problems in NL...
; this problem is called "2SAT". Determining the satisfiability of a formula in which each clause is a Horn clause
Horn clause
In mathematical logic, a Horn clause is a clause with at most one positive literal. They are named after the logician Alfred Horn, who first pointed out the significance of such clauses in 1951...
(i.e. it contains at most one positive literal) is P-complete
P-complete
In complexity theory, the notion of P-complete decision problems is useful in the analysis of both:# which problems are difficult to parallelize effectively, and;# which problems are difficult to solve in limited space....
; this problem is called Horn-satisfiability
Horn-satisfiability
In formal logic, Horn-satisfiability, or HORNSAT, is the problem of deciding whether a given set of propositional Horn clauses is satisfiable....
.
The Cook–Levin theorem states that the Boolean satisfiability problem is NP-complete, and in fact, this was the first decision problem proved to be NP-complete. However, beyond this theoretical significance, efficient and scalable algorithms for SAT that were developed over the last decade have contributed to dramatic advances in our ability to automatically solve problem instances involving tens of thousands of variables and millions of constraints. Examples of such problems in electronic design automation (EDA) include formal equivalence checking
Formal equivalence checking
Formal equivalence checking process is a part of electronic design automation , commonly used during the development of digital integrated circuits, to formally prove that two representations of a circuit design exhibit exactly the same behavior....
, model checking
Model checking
In computer science, model checking refers to the following problem:Given a model of a system, test automatically whether this model meets a given specification....
, formal verification
Formal verification
In the context of hardware and software systems, formal verification is the act of proving or disproving the correctness of intended algorithms underlying a system with respect to a certain formal specification or property, using formal methods of mathematics .- Usage :Formal verification can be...
of pipelined microprocessors
Microprocessor
A microprocessor incorporates the functions of a computer's central processing unit on a single integrated circuit, or at most a few integrated circuits. It is a multipurpose, programmable device that accepts digital data as input, processes it according to instructions stored in its memory, and...
, automatic test pattern generation
Automatic test pattern generation
ATPG is an electronic design automation method/technology used to find an input sequence that, when applied to a digital circuit, enables automatic test equipment to distinguish between the correct circuit behavior and the faulty circuit...
, routing of FPGAs, and so on. A SAT-solving engine is now considered to be an essential component in the EDA toolbox.
NP-completeness
SAT was the first known NP-completeNP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
problem, as proved by Stephen Cook
Stephen Cook
Stephen Arthur Cook is a renowned American-Canadian computer scientist and mathematician who has made major contributions to the fields of complexity theory and proof complexity...
in 1971 (see Cook's theorem for the proof). Until that time, the concept of an NP-complete problem did not even exist. The problem remains NP-complete even if all expressions are written in conjunctive normal form
Conjunctive normal form
In Boolean logic, a formula is in conjunctive normal form if it is a conjunction of clauses, where a clause is a disjunction of literals.As a normal form, it is useful in automated theorem proving...
with 3 variables per clause (3-CNF), yielding the 3SAT problem. This means the expression has the form: AND AND AND ...
where each x is a variable or a negation of a variable, and each variable can appear multiple times in the expression.
A useful property of Cook's reduction is that it preserves the number of accepting answers. For example, if a graph has 17 valid 3-colorings, the SAT formula produced by the reduction will have 17 satisfying assignments.
NP-completeness only refers to the run-time of the worst case instances. Many of the instances that occur in practical applications can be solved much more quickly. See runtime behavior below.
SAT is easier if the formulas are restricted to those in disjunctive normal form
Disjunctive normal form
In boolean logic, a disjunctive normal form is a standardization of a logical formula which is a disjunction of conjunctive clauses. As a normal form, it is useful in automated theorem proving. A logical formula is considered to be in DNF if and only if it is a disjunction of one or more...
, that is, they are disjunction (OR) of terms, where each term is a conjunction (AND) of literals (possibly negated variables). Such a formula is indeed satisfiable if and only if at least one of its terms is satisfiable, and a term is satisfiable if and only if it does not contain both x and NOT x for some variable x. This can be checked in polynomial time.
2-satisfiability
SAT is also easier if the number of literals in a clause is limited to 2, in which case the problem is called 2SAT. This problem can also be solved in polynomial time, and in fact is complete for the class NLNL (complexity)
In computational complexity theory, NL is the complexity class containing decision problems which can be solved by a nondeterministic Turing machine using a logarithmic amount of memory space....
. Similarly, if we limit the number of literals per clause to 2 and change the AND operations to XOR operations, the result is exclusive-or 2-satisfiability, a problem complete for SL
SL (complexity)
In computational complexity theory, SL is the complexity class of problems log-space reducible to USTCON , which is the problem of determining whether there exists a path between two vertices in an undirected graph, otherwise described as the problem of determining whether two vertices are in the...
= L
L (complexity)
In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space...
.
One of the most important restrictions of SAT is HORNSAT, where the formula is a conjunction of Horn clause
Horn clause
In mathematical logic, a Horn clause is a clause with at most one positive literal. They are named after the logician Alfred Horn, who first pointed out the significance of such clauses in 1951...
s. This problem is solved by the polynomial-time Horn-satisfiability
Horn-satisfiability
In formal logic, Horn-satisfiability, or HORNSAT, is the problem of deciding whether a given set of propositional Horn clauses is satisfiable....
algorithm, and is in fact P-complete
P-complete
In complexity theory, the notion of P-complete decision problems is useful in the analysis of both:# which problems are difficult to parallelize effectively, and;# which problems are difficult to solve in limited space....
. It can be seen as P's
P (complexity)
In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds...
version of the Boolean satisfiability problem.
Provided that the complexity classes P and NP are not equal, none of these restrictions are NP-complete, unlike SAT. The assumption that P and NP are not equal is currently not proven.
3-satisfiability
3-satisfiability is a special case of k-satisfiability (k-SAT) or simply satisfiability (SAT), when each clause contains exactly k = 3 literals. It was one of Karp's 21 NP-complete problemsKarp's 21 NP-complete problems
One of the most important results in computational complexity theory was Stephen Cook's 1971 demonstration of the first NP-complete problem, the boolean satisfiability problem...
.
Here is an example, where ¬ indicates negation
Negation
In logic and mathematics, negation, also called logical complement, is an operation on propositions, truth values, or semantic values more generally. Intuitively, the negation of a proposition is true when that proposition is false, and vice versa. In classical logic negation is normally identified...
:
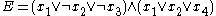
E has two clauses (denoted by parentheses), four variables (x1, x2, x3, x4), and k=3 (three literals per clause).
To solve this instance of the decision problem we must determine whether there is a truth value (TRUE or FALSE) we can assign to each of the variables (x1 through x4) such that the entire expression is TRUE. In this instance, there is such an assignment (x1 = TRUE, x2 = TRUE, x3=TRUE, x4=TRUE), so the answer to this instance is YES. This is one of many possible assignments, with for instance, any set of assignments including x1 = TRUE being sufficient. If there were no such assignment(s), the answer would be NO.
3-SAT is NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
and it is used as a starting point for proving that other problems are also NP-hard
NP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
. This is done by polynomial-time reduction
Polynomial-time reduction
In computational complexity theory a polynomial-time reduction is a reduction which is computable by a deterministic Turing machine in polynomial time. If it is a many-one reduction, it is called a polynomial-time many-one reduction, polynomial transformation, or Karp reduction...
from 3-SAT to the other problem. An example of a problem where this method has been used is the Clique problem
Clique problem
In computer science, the clique problem refers to any of the problems related to finding particular complete subgraphs in a graph, i.e., sets of elements where each pair of elements is connected....
. 3-SAT can be further restricted to One-in-three 3SAT
One-in-three 3SAT
In computational complexity theory, one-in-three 3SAT is an NP-complete problem. The problem is a variant of the 3-satisfiability problem . Like 3SAT, the input instance is a collection of clauses, where each clause consists of exactly three literals, and each literal is either a variable or its...
, where we ask if exactly one of the literals in each clause is true, rather than at least one. This restriction remains NP-complete.
There is a simple randomized algorithm due to that runs in time
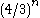where n is the number of clauses and succeeds with high probability to correctly decide 3-Sat.The exponential time hypothesis
Exponential time hypothesis
In computational complexity theory, the exponential time hypothesis is an unproven computational hardness assumption formalized by stating that 3-SAT cannot be solved in subexponential time in the worst case. The exponential time hypothesis, if true, would imply that P ≠ NP...
is that no algorithm can solve 3-Sat in time
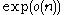.Horn-satisfiability
A clause is Horn if it contains at most one positive literal. Such clauses are of interest because they are able to express implicationEntailment
In logic, entailment is a relation between a set of sentences and a sentence. Let Γ be a set of one or more sentences; let S1 be the conjunction of the elements of Γ, and let S2 be a sentence: then, Γ entails S2 if and only if S1 and not-S2 are logically inconsistent...
of one variable from a set of other variables. Indeed, one such clause
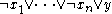can be rewritten as 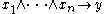, that is, if 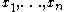are all true, then y needs to be true as well.The problem of deciding whether a set of Horn clauses is satisfiable is in P. This problem can indeed be solved by a single step of the Unit propagation
Unit propagation
Unit propagation or the one-literal rule is a procedure of automated theorem proving that can simplify a set of clauses.-Definition:...
, which produces the single minimal (w.r.t. the set of literal assigned to true) model of the set of Horn clauses.
A generalization of the class of Horn formulae is that of renamable-Horn formulae, which is the set of formulae that can be placed in Horn form by replacing some variables with their respective negation. Checking the existence of such a replacement can be done in linear time; therefore, the satisfiability of such formulae is in P as it can be solved by first performing this replacement and then checking the satisfiability of the resulting Horn formula.
XOR-satisfiability
Another special case are problems where each clause only contains exclusive or operators. Because the exclusive or operation is equivalent to addition on a Galois field of size 2 (see also modular arithmeticModular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
), the clauses can be viewed as a system of linear equations and corresponding methods such as Gaussian elimination
Gaussian elimination
In linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...
can be used to find the solution.
Schaefer's dichotomy theorem
The restrictions above (CNF, 2CNF, 3CNF, Horn) bound the considered formulae to be conjunction of subformulae; each restriction states a specific form for all subformulae: for example, only binary clauses can be subformulae in 2CNF.Schaefer's dichotomy theorem states that, for any restriction to Boolean operators that can be used to form these subformulae, the corresponding satisfiability problem is in P or NP-complete. The membership in P of the satisfiability of 2CNF and Horn formulae are special cases of this theorem.
Runtime behavior
As mentioned briefly above, though the problem is NP-complete, many practical instances can be solved much more quickly. Many practical problems are actually "easy", so the SAT solver can easily find a solution, or prove that none exists, relatively quickly, even though the instance has thousands of variables and tens of thousands of constraints. Other much smaller problems exhibit run-times that are exponential in the problem size, and rapidly become impractical. Unfortunately, there is no reliable way to tell the difficulty of the problem without trying it. Therefore, almost all SAT solvers include time-outs, so they will terminate even if they cannot find a solution. Finally, different SAT solvers will find different instances easy or hard, and some excel at proving unsatisfiability, and others at finding solutions. All of these behaviors can be seen in the SAT solving contests.Extensions of SAT
An extension that has gained significant popularity since 2003 is Satisfiability modulo theoriesSatisfiability Modulo Theories
In computer science, the Satisfiability Modulo Theories problem is a decision problem for logical formulas with respect to combinations of background theories expressed in classical first-order logic with equality...
(SMT) that can enrich CNF formulas with linear constraints, arrays, all-different constraints, uninterpreted function
Uninterpreted function
In mathematical logic, an uninterpreted function or function symbol is one that has no other property than its name and arity. Function symbols are used, together with constants and variables, to form terms....
s, etc. Such extensions typically remain NP-complete, but very efficient solvers are now available that can handle many such kinds of constraints.
The satisfiability problem becomes more difficult (PSPACE-complete) if we extend our logic to include second-order Booleans, allowing quantifiers such as "for all" and "there exists" that bind the Boolean variables. An example of such an expression would be:
SAT itself uses only
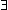quantifiers. If we allow only 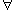quantifiers, it becomes the Co-NP-completeCo-NP-complete
In complexity theory, computational problems that are co-NP-complete are those that are the hardest problems in co-NP, in the sense that they are the ones most likely not to be in P...
tautology
Tautology (logic)
In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...
problem. If we allow both, the problem is called the quantified Boolean formula problem (QBF), which can be shown to be PSPACE-complete
PSPACE-complete
In complexity theory, a decision problem is PSPACE-complete if it is in the complexity class PSPACE, and every problem in PSPACE can be reduced to it in polynomial time...
. It is widely believed that PSPACE-complete problems are strictly harder than any problem in NP, although this has not yet been proved.
A number of variants deal with the number of variable assignments making the formula true. Ordinary SAT asks if there is at least one such assignment. MAJSAT, which asks if the majority of all assignments make the formula true, is complete for PP
PP (complexity)
In complexity theory, PP is the class of decision problems solvable by a probabilistic Turing machine in polynomial time, with an error probability of less than 1/2 for all instances. The abbreviation PP refers to probabilistic polynomial time...
, a probabilistic class. The problem of how many variable assignments satisfy a formula, not a decision problem, is in #P
Sharp-P
In computational complexity theory, the complexity class #P is the set of the counting problems associated with the decision problems in the set NP. More formally, #P is the class of function problems of the form "compute ƒ," where ƒ is the number of accepting paths of a nondeterministic...
. UNIQUE-SAT or USAT or Unambiguous SAT is the problem of determining whether a formula known to have either zero or one satisfying assignments has zero or has one. Although this problem seems easier, it has been shown
Valiant-Vazirani theorem
The Valiant–Vazirani theorem is a theorem in computational complexity theory. It was proven by Leslie Valiant and Vijay Vazirani in their paper titled "NP is as easy as detecting unique solutions" published in 1986...
that if there is a practical (randomized polynomial-time) algorithm to solve this problem, then all problems in NP can be solved just as easily.
The maximum satisfiability problem
Maximum satisfiability problem
In computational complexity theory, the Maximum Satisfiability problem is the problem of determining the maximum number of clauses, of a given Boolean formula, that can be satisfied by some assignment...
, an FNP
FNP (complexity)
In computational complexity theory, the complexity class FNP is the function problem extension of the decision problem class NP. The name is somewhat of a misnomer, since technically it is a class of binary relations, not functions, as the following formal definition explains:This definition does...
generalization of SAT, asks for the maximum number of clauses which can be satisfied by any assignment. It has efficient approximation algorithm
Approximation algorithm
In computer science and operations research, approximation algorithms are algorithms used to find approximate solutions to optimization problems. Approximation algorithms are often associated with NP-hard problems; since it is unlikely that there can ever be efficient polynomial time exact...
s, but is NP-hard to solve exactly. Worse still, it is APX
APX
In complexity theory the class APX is the set of NP optimization problems that allow polynomial-time approximation algorithms with approximation ratio bounded by a constant...
-complete, meaning there is no polynomial-time approximation scheme
Polynomial-time approximation scheme
In computer science, a polynomial-time approximation scheme is a type of approximation algorithm for optimization problems ....
(PTAS) for this problem unless P=NP.
Self-reducibility
An algorithm which correctly answers if an instance of SAT is solvable can be used to find a satisfying assignment. First, the question is asked on formula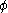. If the answer is "no", the formula is unsatisfable. Otherwise, the question is asked on 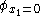, i.e. the first variable is assumed to be 0. If the answer is "no", it is assumed that 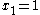, otherwise 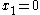. Values of other variables are found subsequently.This property is used in several theorems in complexity theory:
(
Algorithms for solving SAT
There are two classes of high-performance algorithms for solving instances of SAT in practice: the conflict-driven clause learning algorithm, which can be viewed as a modern variant of the DPLL algorithmDPLL algorithm
The Davis–Putnam–Logemann–Loveland algorithm is a complete, backtracking-based algorithm for deciding the satisfiability of propositional logic formulae in conjunctive normal form, i.e. for solving the CNF-SAT problem....
(well known implementation include Chaff
Chaff algorithm
Chaff is an algorithm for solving instances of the Boolean satisfiability problem in programming. It was designed by researchers at Princeton University, USA...
, GRASP
GRASP (SAT solver)
GRASP is a well known SAT instance solver. It was developed by João Marques Silva, a Portuguese computer science researcher. It stands for Generic seaRch Algorithm for the Satisfiability Problem.- References :...
) and stochastic local search
Local search (constraint satisfaction)
In constraint satisfaction, local search is an incomplete method for finding a solution to a problem. It is based on iteratively improving an assignment of the variables until all constraints are satisfied. In particular, local search algorithms typically modify the value of a variable in an...
algorithms, such as WalkSAT
WalkSAT
GSAT and WalkSat are local search algorithms to solve Boolean satisfiability problems.Both algorithms work on formulae that are in, or have been converted into, conjunctive normal form. They start by assigning a random value to each variable. If the assignment satisfies all clauses, the algorithm...
.
A DPLL SAT solver employs a systematic backtracking search procedure to explore the (exponentially sized) space of variable assignments looking for satisfying assignments. The basic search procedure was proposed in two seminal papers in the early 60s (see references below) and is now commonly referred to as the Davis–Putnam–Logemann–Loveland algorithm (“DPLL” or “DLL”). Theoretically, exponential lower bounds have been proved for the DPLL family of algorithms.
Modern SAT solvers (developed in the last ten years) come in two flavors: "conflict-driven" and "look-ahead". Conflict-driven solvers augment the basic DPLL search algorithm with efficient conflict analysis, clause learning, non-chronological backtracking (aka backjumping
Backjumping
In backtracking algorithms, backjumping is a technique that reduces search space, therefore increasing efficiency. While backtracking always goes up one level in the search tree when all values for a variable have been tested, backjumping may go up more levels...
), as well as "two-watched-literals" unit propagation, adaptive branching, and random restarts. These "extras" to the basic systematic search have been empirically shown to be essential for handling the large SAT instances that arise in electronic design automation
Electronic design automation
Electronic design automation is a category of software tools for designing electronic systems such as printed circuit boards and integrated circuits...
(EDA). Look-ahead solvers have especially strengthened reductions (going beyond unit-clause propagation) and the heuristics, and they are generally stronger than conflict-driven solvers on hard instances (while conflict-driven solvers can be much better on large instances which actually have an easy instance inside).
Modern SAT solvers are also having significant impact on the fields of software verification, constraint solving in artificial intelligence, and operations research, among others. Powerful solvers are readily available as free and open source software
Free and open source software
Free and open-source software or free/libre/open-source software is software that is liberally licensed to grant users the right to use, study, change, and improve its design through the availability of its source code...
. In particular, the conflict-driven MiniSAT, which was relatively successful at the 2005 SAT competition, only has about 600 lines of code. An example for look-ahead solvers is march_dl, which won a prize at the 2007 SAT competition.
Certain types of large random satisfiable instances of SAT can be solved by survey propagation (SP). Particularly in hardware design and verification applications, satisfiability and other logical properties of a given propositional formula are sometimes decided based on a representation of the formula as a binary decision diagram
Binary decision diagram
In the field of computer science, a binary decision diagram or branching program, like a negation normal form or a propositional directed acyclic graph , is a data structure that is used to represent a Boolean function. On a more abstract level, BDDs can be considered as a compressed...
(BDD).
Propositional satisfiability has various generalisations, including satisfiability for quantified Boolean formula problem, for first- and second-order logic
Second-order logic
In logic and mathematics second-order logic is an extension of first-order logic, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic and type theory....
, constraint satisfaction problem
Constraint satisfaction problem
Constraint satisfaction problems s are mathematical problems defined as a set of objects whose state must satisfy a number of constraints or limitations. CSPs represent the entities in a problem as a homogeneous collection of finite constraints over variables, which is solved by constraint...
s, 0-1 integer programming, and maximum satisfiability problem
Maximum satisfiability problem
In computational complexity theory, the Maximum Satisfiability problem is the problem of determining the maximum number of clauses, of a given Boolean formula, that can be satisfied by some assignment...
.
Many other decision problems, such as graph coloring
Graph coloring
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
problems, planning problems
Automated planning and scheduling
Automated planning and scheduling is a branch of artificial intelligence that concerns the realization of strategies or action sequences, typically for execution by intelligent agents, autonomous robots and unmanned vehicles. Unlike classical control and classification problems, the solutions are...
, and scheduling problems, can be easily encoded into SAT.
External links
More information on SAT:SAT Applications:
- WinSAT v2.04: A Windows-based SAT application made particularly for researchers.
SAT Solvers:
- Chaff
- HyperSAT
- Spear
- The MiniSAT Solver
- UBCSAT
- Sat4j
- RSat
- Fast SAT Solver - simple but fast implementation of SAT solver based on genetic algorithmGenetic algorithmA genetic algorithm is a search heuristic that mimics the process of natural evolution. This heuristic is routinely used to generate useful solutions to optimization and search problems...
s - PicoSAT
- CryptoMiniSat
International Conference on Theory and Applications of Satisfiability Testing:
Publications:
Benchmarks:
- Forced Satisfiable SAT Benchmarks
- IBM Formal Verification SAT Benchmarks
- SATLIB
- Software Verification Benchmarks
- Fadi Aloul SAT Benchmarks
SAT solving in general:
- http://www.satlive.org
- http://www.satisfiability.org
Evaluation of SAT solvers:
----
This article includes material from a column in the ACM SIGDA e-newsletter by Prof. Karem Sakallah
Original text is available here
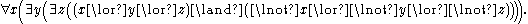
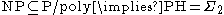