Horn-satisfiability
Encyclopedia
In formal logic
, Horn-satisfiability, or HORNSAT, is the problem of deciding whether a given set of propositional Horn clause
s is satisfiable.
A Horn clause is a clause
with at most one positive literal, called the head of the clause, and any number of negative literals, forming the body of the clause. A Horn formula is a propositional formula
formed by conjunction of Horn clauses.
The problem of Horn satisfiability is solvable in linear time. A polynomial-time algorithm for Horn satisfiability is based on the rule of unit propagation
: if the formula contains a clause composed of a single literal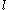
(a unit clause), then all clauses containing 
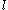are removed, and all clauses containing 
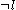have this literal removed. The result of the second rule may itself be a unit clause, which is propagated in the same manner. If there are no unit clauses, the formula can be satisfied by simply setting all remaining variables negative. The formula is unsatisfiable if this transformation generates a pair of opposite unit clauses 
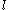and 
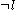. Horn satisfiability is actually one of the "hardest" or "most expressive" problems which is known to be computable in polynomial time, in the sense that it is a P-complete
problem.
This algorithm also allows determining a truth assignment of satisfiable Horn formulae: all variables contained in a unit clause are set to the value satisfying that unit clause; all other literals are set to false. The resulting assignment is the minimal model of the Horn formula, that is, the assignment having a minimal set of variables assigned to true, where comparison is made using set containment.
Using a linear algorithm for unit propagation, the algorithm is linear in the size of the formula.
A generalization of the class of Horn formulae is that of renamable-Horn formulae, which is the set of formulae that can be placed in Horn form by replacing some variables with their respective negation. Checking the existence of such a replacement can be done in linear time; therefore, the satisfiability of such formulae is in P as it can be solved by first performing this replacement and then checking the satisfiability of the resulting Horn formula.
The Horn satisfiability problem can also be asked for propositional many-valued logics. The algorithms are not usually linear, but some are polynomial; see Hähnle (2001 or 2003) for a survey.
Formal logic
Classical or traditional system of determining the validity or invalidity of a conclusion deduced from two or more statements...
, Horn-satisfiability, or HORNSAT, is the problem of deciding whether a given set of propositional Horn clause
Horn clause
In mathematical logic, a Horn clause is a clause with at most one positive literal. They are named after the logician Alfred Horn, who first pointed out the significance of such clauses in 1951...
s is satisfiable.
A Horn clause is a clause
Clause (logic)
In logic, a clause is a finite disjunction ofliterals. Clausesare usually written as follows, where the symbols l_i areliterals:l_1 \vee \cdots \vee l_nIn some cases, clauses are written as sets of literals, so that clause above...
with at most one positive literal, called the head of the clause, and any number of negative literals, forming the body of the clause. A Horn formula is a propositional formula
Propositional formula
In propositional logic, a propositional formula is a type of syntactic formula which is well formed and has a truth value. If the values of all variables in a propositional formula are given, it determines a unique truth value...
formed by conjunction of Horn clauses.
The problem of Horn satisfiability is solvable in linear time. A polynomial-time algorithm for Horn satisfiability is based on the rule of unit propagation
Unit propagation
Unit propagation or the one-literal rule is a procedure of automated theorem proving that can simplify a set of clauses.-Definition:...
: if the formula contains a clause composed of a single literal
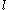(a unit clause), then all clauses containing 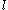are removed, and all clauses containing 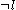have this literal removed. The result of the second rule may itself be a unit clause, which is propagated in the same manner. If there are no unit clauses, the formula can be satisfied by simply setting all remaining variables negative. The formula is unsatisfiable if this transformation generates a pair of opposite unit clauses 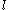and 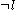. Horn satisfiability is actually one of the "hardest" or "most expressive" problems which is known to be computable in polynomial time, in the sense that it is a P-completeP-complete
In complexity theory, the notion of P-complete decision problems is useful in the analysis of both:# which problems are difficult to parallelize effectively, and;# which problems are difficult to solve in limited space....
problem.
This algorithm also allows determining a truth assignment of satisfiable Horn formulae: all variables contained in a unit clause are set to the value satisfying that unit clause; all other literals are set to false. The resulting assignment is the minimal model of the Horn formula, that is, the assignment having a minimal set of variables assigned to true, where comparison is made using set containment.
Using a linear algorithm for unit propagation, the algorithm is linear in the size of the formula.
A generalization of the class of Horn formulae is that of renamable-Horn formulae, which is the set of formulae that can be placed in Horn form by replacing some variables with their respective negation. Checking the existence of such a replacement can be done in linear time; therefore, the satisfiability of such formulae is in P as it can be solved by first performing this replacement and then checking the satisfiability of the resulting Horn formula.
The Horn satisfiability problem can also be asked for propositional many-valued logics. The algorithms are not usually linear, but some are polynomial; see Hähnle (2001 or 2003) for a survey.