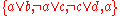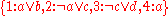Unit propagation
Encyclopedia
Unit propagation or the one-literal rule (OLR) is a procedure
of automated theorem proving
that can simplify a set of (usually propositional) clauses
.
. If a set of clauses contains the unit clause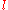
, the other clauses are simplified by the application of the two following rules:
The application of these two rules lead to a new set of clauses that is equivalent to the old one. For example, the following set of clauses can be simplified by unit propagation because it contains the unit clause
.
Since
contains the literal 
, this clause can be removed altogether. Since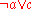 
contains the negation of the literal in the unit clause, this literal can be removed from the clause. The unit clause 
is not removed; this would make the resulting set not equivalent to the original one; this clause can be removed if already stored in some other form (see section "Using a partial model"). The effect of unit propagation can be summarized as follows.
The resulting set of clauses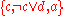
is equivalent to the above one. The new unit clause 
that results from unit propagation can be used for a further application of unit propagation, which would transform 
into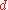 
.
, in which one of the two resolvents must always be a unit clause. As for resolution, unit propagation is a correct inference rule, in that it never produces a new clause that was not entailed by the old ones. The difference between unit propagation and resolution are:
Resolution calculi that include subsumption
can model rule one by subsumption and rule two by a unit resolution step, followed by subsumption.
Unit propagation, applied repeatedly as new unit clauses are generated, is a complete satisfiability algorithm for sets of propositional Horn clause
s; it also generates a minimal model for the set if satisfiable: see Horn-satisfiability
.
would be added to the partial model; the simplification of the set of clause would then proceed as above with the difference that the unit clause 
is now removed from the set. The resulting set of clause is equivalent to the original one under the assumption of validity of the literals in the partial model.
in the total size of the set to check , which is defined to be the sum of the size of all clauses, where the size of each clause is the number of literals it contains.
Unit propagation can however be done in linear time by storing, for each variable, the list of clauses in which each literal is contained. For example, the set above can be represented by numbering each clause as follows:
and then storing, for each variable, the list of clauses containing the variable or its negation:
This simple data structure can be built in time linear in the size of the set, and allows finding all clauses containing a variable very easily. Unit propagation of a literal can be performed efficiently by scanning only the list of clauses containing the variable of the literal. More precisely, the total running time for doing unit propagation for all unit clauses is linear in the size of the set of clauses.
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
of automated theorem proving
Automated theorem proving
Automated theorem proving or automated deduction, currently the most well-developed subfield of automated reasoning , is the proving of mathematical theorems by a computer program.- Decidability of the problem :...
that can simplify a set of (usually propositional) clauses
Clause (logic)
In logic, a clause is a finite disjunction ofliterals. Clausesare usually written as follows, where the symbols l_i areliterals:l_1 \vee \cdots \vee l_nIn some cases, clauses are written as sets of literals, so that clause above...
.
Definition
The procedure is based on unit clauses, i.e. clauses that are composed of a single literalLiteral (mathematical logic)
In mathematical logic, a literal is an atomic formula or its negation.The definition mostly appears in proof theory , e.g...
. If a set of clauses contains the unit clause
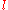, the other clauses are simplified by the application of the two following rules:- every clause containing
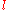is removed; - in every clause that contains
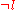this literal is deleted.
The application of these two rules lead to a new set of clauses that is equivalent to the old one. For example, the following set of clauses can be simplified by unit propagation because it contains the unit clause
.
Since
contains the literal , this clause can be removed altogether. Since 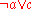contains the negation of the literal in the unit clause, this literal can be removed from the clause. The unit clause is not removed; this would make the resulting set not equivalent to the original one; this clause can be removed if already stored in some other form (see section "Using a partial model"). The effect of unit propagation can be summarized as follows.  |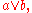
 |
 |
 |
 |
|
| (removed) | ( deleted) |
(unchanged) | (unchanged) | ||
 |
 |
 |
 |
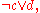The resulting set of clauses
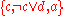is equivalent to the above one. The new unit clause that results from unit propagation can be used for a further application of unit propagation, which would transform into 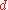.Unit propagation and resolution
The second rule of unit propagation can be seen as a restricted form of resolutionResolution (logic)
In mathematical logic and automated theorem proving, resolution is a rule of inference leading to a refutation theorem-proving technique for sentences in propositional logic and first-order logic...
, in which one of the two resolvents must always be a unit clause. As for resolution, unit propagation is a correct inference rule, in that it never produces a new clause that was not entailed by the old ones. The difference between unit propagation and resolution are:
- resolution is a complete refutation procedure while unit propagation is not; in other words, even if a set of clause is contradictory, unit propagation may not generate an inconsistency;
- the two clauses that are resolved cannot in general be removed after the generated clause is added to the set; on the contrary, the non-unit clause involved in a unit propagation can be removed when its simplification is added to the set;
- resolution does not in general include the first rule used in unit propagation.
Resolution calculi that include subsumption
Subsumption
Subsumption may refer to:* A minor premise in symbolic logic * The Liskov substitution principle in object-oriented programming* Subsumption architecture in robotics...
can model rule one by subsumption and rule two by a unit resolution step, followed by subsumption.
Unit propagation, applied repeatedly as new unit clauses are generated, is a complete satisfiability algorithm for sets of propositional Horn clause
Horn clause
In mathematical logic, a Horn clause is a clause with at most one positive literal. They are named after the logician Alfred Horn, who first pointed out the significance of such clauses in 1951...
s; it also generates a minimal model for the set if satisfiable: see Horn-satisfiability
Horn-satisfiability
In formal logic, Horn-satisfiability, or HORNSAT, is the problem of deciding whether a given set of propositional Horn clauses is satisfiable....
.
Using a partial model
The unit clauses that are present in a set of clauses or can be derived from it can be stored in form of a partial model (this partial model may also contain other literals, depending on the application). In this case, unit propagation is performed based on the literals of the partial model, and unit clauses are removed if their literal is in the model. In the example above, the unit clause would be added to the partial model; the simplification of the set of clause would then proceed as above with the difference that the unit clause is now removed from the set. The resulting set of clause is equivalent to the original one under the assumption of validity of the literals in the partial model.Complexity
The direct implementation of unit propagation takes time quadraticQuadratic growth
In mathematics, a function or sequence is said to exhibit quadratic growth when its values are proportional to the square of the function argument or sequence position, in the limit as the argument or sequence position goes to infinity...
in the total size of the set to check , which is defined to be the sum of the size of all clauses, where the size of each clause is the number of literals it contains.
Unit propagation can however be done in linear time by storing, for each variable, the list of clauses in which each literal is contained. For example, the set above can be represented by numbering each clause as follows:
and then storing, for each variable, the list of clauses containing the variable or its negation:
This simple data structure can be built in time linear in the size of the set, and allows finding all clauses containing a variable very easily. Unit propagation of a literal can be performed efficiently by scanning only the list of clauses containing the variable of the literal. More precisely, the total running time for doing unit propagation for all unit clauses is linear in the size of the set of clauses.
See also
- Horn satisfiabilityHorn-satisfiabilityIn formal logic, Horn-satisfiability, or HORNSAT, is the problem of deciding whether a given set of propositional Horn clauses is satisfiable....
- Horn clauseHorn clauseIn mathematical logic, a Horn clause is a clause with at most one positive literal. They are named after the logician Alfred Horn, who first pointed out the significance of such clauses in 1951...
- Automated theorem provingAutomated theorem provingAutomated theorem proving or automated deduction, currently the most well-developed subfield of automated reasoning , is the proving of mathematical theorems by a computer program.- Decidability of the problem :...
- DPLL algorithmDPLL algorithmThe Davis–Putnam–Logemann–Loveland algorithm is a complete, backtracking-based algorithm for deciding the satisfiability of propositional logic formulae in conjunctive normal form, i.e. for solving the CNF-SAT problem....