
Resolution (logic)
Encyclopedia
In mathematical logic
and automated theorem proving
, resolution is a rule of inference
leading to a refutation
theorem-proving technique for sentences in propositional logic and first-order logic
. In other words, iteratively applying the resolution rule in a suitable way allows for telling whether a propositional formula
is satisfiable and for proving that a first-order formula is unsatisfiable; this method may prove the satisfiability of a first-order satisfiable formula, but not always, as it is the case for all methods for first-order logic. Resolution was introduced by John Alan Robinson
in 1965.
rule that produces a new clause implied by two clauses
containing complementary literals. A literal
is a propositional variable or the negation of a propositional variable. Two literals are said to be complements if one is the negation of the other (in the following,
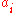 is taken to be the complement to
is taken to be the complement to 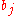 ). The resulting clause contains all the literals that do not have complements.
). The resulting clause contains all the literals that do not have complements.
Formally: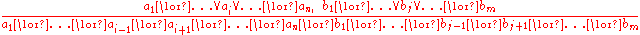
where
The clause produced by the resolution rule is called the resolvent of the two input clauses.
When the two clauses contain more than one pair of complementary literals, the resolution rule can be applied (independently) for each such pair. However, only the pair of literals that are resolved upon can be removed: all other pairs of literals remain in the resolvent clause. Note that resolving any two clauses that can be resolved over more than one variable always results in a tautology
.
Modus ponens
can be seen as a special case of resolution of a one-literal clause and a two-literal clause.
, the resolution rule yields a sound and complete algorithm for deciding the satisfiability of a propositional formula, and, by extension, the validity
of a sentence under a set of axioms.
This resolution technique uses proof by contradiction and is based on the fact that any sentence in propositional logic can be transformed into an equivalent sentence in conjunctive normal form
. The steps are as follows.
One instance of this algorithm is the original Davis–Putnam algorithm
that was later refined into the DPLL algorithm
that removed the need for explicit representation of the resolvents.
This description of the resolution technique uses a set S as the underlying data-structure to represent resolution derivations. Lists, Trees and Directed Acyclic Graphs are other possible and common alternatives. Tree representations are more faithful to the fact that the resolution rule is binary. Together with a sequent notation for clauses, a tree representation also makes it clear to see how the resolution rule is related to a special case of the cut-rule, restricted to atomic cut-formulas. However, tree representations are not as compact as set or list representations, because they explicitly show redundant subderivations of clauses that are used more than once in the derivation of the empty clause. Graph representations can be as compact in the number of clauses as list representations and they also store structural information regarding which clauses were resolved to derive each resolvent.
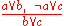
In English: Suppose is false. In order for the premise
is false. In order for the premise  to be true,
to be true,  must be true.
must be true.
Alternatively, suppose is true. In order for the premise
is true. In order for the premise 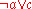 to be true,
to be true,  must be true. Therefore regardless of falsehood or veracity of
must be true. Therefore regardless of falsehood or veracity of  , if both premises hold, then the conclusion
, if both premises hold, then the conclusion  is true.
is true.
s of logical inference
down to a single rule.
To understand how resolution works, consider the following example syllogism of term logic
:
Or, more generally:
To recast the reasoning using the resolution technique, first the clauses must be converted to conjunctive normal form
. In this form, all quantification
becomes implicit: universal quantifiers
on variables (X, Y, …) are simply omitted as understood, while existentially-quantified
variables are replaced by Skolem functions.
So the question is, how does the resolution technique derive the last clause from the first two? The rule is simple:
To apply this rule to the above example, we find the predicate P occurs in negated form
in the first clause, and in non-negated form
in the second clause. X is an unbound variable, while a is a bound value (term). Unifying the two produces the substitution
Discarding the unified predicates, and applying this substitution to the remaining predicates (just Q(X), in this case), produces the conclusion:
For another example, consider the syllogistic form
Or more generally,
In CNF, the antecedents become:
(Note that the variable in the second clause was renamed to make it clear that variables in different clauses are distinct.)
Now, unifying Q(X) in the first clause with ¬Q(Y) in the second clause means that X and Y become the same variable anyway. Substituting this into the remaining clauses and combining them gives the conclusion:
The resolution rule, as defined by Robinson, also incorporated factoring, which unifies two literals in the same clause, before or during the application of resolution as defined above. The resulting inference rule is refutation complete, in that a set of clauses is unsatisfiable if and only if there exists a derivation of the empty clause using resolution alone.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
and automated theorem proving
Automated theorem proving
Automated theorem proving or automated deduction, currently the most well-developed subfield of automated reasoning , is the proving of mathematical theorems by a computer program.- Decidability of the problem :...
, resolution is a rule of inference
Inference
Inference is the act or process of deriving logical conclusions from premises known or assumed to be true. The conclusion drawn is also called an idiomatic. The laws of valid inference are studied in the field of logic.Human inference Inference is the act or process of deriving logical conclusions...
leading to a refutation
Reductio ad absurdum
In logic, proof by contradiction is a form of proof that establishes the truth or validity of a proposition by showing that the proposition's being false would imply a contradiction...
theorem-proving technique for sentences in propositional logic and first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
. In other words, iteratively applying the resolution rule in a suitable way allows for telling whether a propositional formula
Propositional formula
In propositional logic, a propositional formula is a type of syntactic formula which is well formed and has a truth value. If the values of all variables in a propositional formula are given, it determines a unique truth value...
is satisfiable and for proving that a first-order formula is unsatisfiable; this method may prove the satisfiability of a first-order satisfiable formula, but not always, as it is the case for all methods for first-order logic. Resolution was introduced by John Alan Robinson
J. Alan Robinson
John Alan Robinson is a philosopher , mathematician and computer scientist. He is University Professor Emeritus at Syracuse University, United States....
in 1965.
Resolution rule
The resolution rule in propositional logic is a single valid inferenceInference
Inference is the act or process of deriving logical conclusions from premises known or assumed to be true. The conclusion drawn is also called an idiomatic. The laws of valid inference are studied in the field of logic.Human inference Inference is the act or process of deriving logical conclusions...
rule that produces a new clause implied by two clauses
Clause (logic)
In logic, a clause is a finite disjunction ofliterals. Clausesare usually written as follows, where the symbols l_i areliterals:l_1 \vee \cdots \vee l_nIn some cases, clauses are written as sets of literals, so that clause above...
containing complementary literals. A literal
Literal (mathematical logic)
In mathematical logic, a literal is an atomic formula or its negation.The definition mostly appears in proof theory , e.g...
is a propositional variable or the negation of a propositional variable. Two literals are said to be complements if one is the negation of the other (in the following,
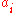 is taken to be the complement to
is taken to be the complement to 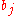 ). The resulting clause contains all the literals that do not have complements.
). The resulting clause contains all the literals that do not have complements.Formally:
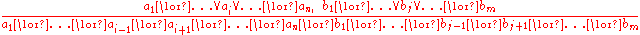
where
- all
 s and
s and  s are literals,
s are literals, -
 is the complement to
is the complement to 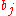 , and
, and - the dividing line stands for entails
The clause produced by the resolution rule is called the resolvent of the two input clauses.
When the two clauses contain more than one pair of complementary literals, the resolution rule can be applied (independently) for each such pair. However, only the pair of literals that are resolved upon can be removed: all other pairs of literals remain in the resolvent clause. Note that resolving any two clauses that can be resolved over more than one variable always results in a tautology
Tautology
Tautology may refer to:*Tautology , using different words to say the same thing even if the repetition does not provide clarity. Tautology also means a series of self-reinforcing statements that cannot be disproved because the statements depend on the assumption that they are already...
.
Modus ponens
Modus ponens
In classical logic, modus ponendo ponens or implication elimination is a valid, simple argument form. It is related to another valid form of argument, modus tollens. Both Modus Ponens and Modus Tollens can be mistakenly used when proving arguments...
can be seen as a special case of resolution of a one-literal clause and a two-literal clause.
A resolution technique
When coupled with a complete search algorithmSearch algorithm
In computer science, a search algorithm is an algorithm for finding an item with specified properties among a collection of items. The items may be stored individually as records in a database; or may be elements of a search space defined by a mathematical formula or procedure, such as the roots...
, the resolution rule yields a sound and complete algorithm for deciding the satisfiability of a propositional formula, and, by extension, the validity
Validity
In logic, argument is valid if and only if its conclusion is entailed by its premises, a formula is valid if and only if it is true under every interpretation, and an argument form is valid if and only if every argument of that logical form is valid....
of a sentence under a set of axioms.
This resolution technique uses proof by contradiction and is based on the fact that any sentence in propositional logic can be transformed into an equivalent sentence in conjunctive normal form
Conjunctive normal form
In Boolean logic, a formula is in conjunctive normal form if it is a conjunction of clauses, where a clause is a disjunction of literals.As a normal form, it is useful in automated theorem proving...
. The steps are as follows.
- All sentences in the knowledge base and the negation of the sentence to be proved (the conjecture) are conjunctively connected.
- The resulting sentence is transformed into a conjunctive normal form with the conjuncts viewed as elements in a set, S, of clauses.
- For example
 gives rise to the set
gives rise to the set 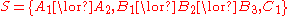 .
.
- For example
- The resolution rule is applied to all possible pairs of clauses that contain complementary literals. After each application of the resolution rule, the resulting sentence is simplified by removing repeated literals. If the sentence contains complementary literals, it is discarded (as a tautologyTautology (logic)In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...
). If not, and if it is not yet present in the clause set S, it is added to S, and is considered for further resolution inferences. - If after applying a resolution rule the empty clause is derived, the original formula is unsatisfiable (or contradictory), and hence it can be concluded that the initial conjecture follows from the axioms.
- If, on the other hand, the empty clause cannot be derived, and the resolution rule cannot be applied to derive any more new clauses, the conjecture is not a theorem of the original knowledge base.
One instance of this algorithm is the original Davis–Putnam algorithm
Davis–Putnam algorithm
The Davis–Putnam algorithm was developed by Martin Davis and Hilary Putnam for checking the validity of a first-order logic formula using a resolution-based decision procedure for propositional logic. Since the set of valid first-order formulas is recursively enumerable but not recursive, there...
that was later refined into the DPLL algorithm
DPLL algorithm
The Davis–Putnam–Logemann–Loveland algorithm is a complete, backtracking-based algorithm for deciding the satisfiability of propositional logic formulae in conjunctive normal form, i.e. for solving the CNF-SAT problem....
that removed the need for explicit representation of the resolvents.
This description of the resolution technique uses a set S as the underlying data-structure to represent resolution derivations. Lists, Trees and Directed Acyclic Graphs are other possible and common alternatives. Tree representations are more faithful to the fact that the resolution rule is binary. Together with a sequent notation for clauses, a tree representation also makes it clear to see how the resolution rule is related to a special case of the cut-rule, restricted to atomic cut-formulas. However, tree representations are not as compact as set or list representations, because they explicitly show redundant subderivations of clauses that are used more than once in the derivation of the empty clause. Graph representations can be as compact in the number of clauses as list representations and they also store structural information regarding which clauses were resolved to derive each resolvent.
A simple example
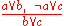
In English: Suppose
 is false. In order for the premise
is false. In order for the premise  to be true,
to be true,  must be true.
must be true.Alternatively, suppose
 is true. In order for the premise
is true. In order for the premise 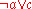 to be true,
to be true,  must be true. Therefore regardless of falsehood or veracity of
must be true. Therefore regardless of falsehood or veracity of  , if both premises hold, then the conclusion
, if both premises hold, then the conclusion  is true.
is true.Resolution in first order logic
In first order logic, resolution condenses the traditional syllogismSyllogism
A syllogism is a kind of logical argument in which one proposition is inferred from two or more others of a certain form...
s of logical inference
Rule of inference
In logic, a rule of inference, inference rule, or transformation rule is the act of drawing a conclusion based on the form of premises interpreted as a function which takes premises, analyses their syntax, and returns a conclusion...
down to a single rule.
To understand how resolution works, consider the following example syllogism of term logic
Term logic
In philosophy, term logic, also known as traditional logic or aristotelian logic, is a loose name for the way of doing logic that began with Aristotle and that was dominant until the advent of modern predicate logic in the late nineteenth century...
:
- All Greeks are Europeans.
- Homer is a Greek.
- Therefore, Homer is a European.
Or, more generally:
-
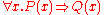
-
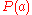
- Therefore,
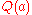
To recast the reasoning using the resolution technique, first the clauses must be converted to conjunctive normal form
Conjunctive normal form
In Boolean logic, a formula is in conjunctive normal form if it is a conjunction of clauses, where a clause is a disjunction of literals.As a normal form, it is useful in automated theorem proving...
. In this form, all quantification
Quantification
Quantification has several distinct senses. In mathematics and empirical science, it is the act of counting and measuring that maps human sense observations and experiences into members of some set of numbers. Quantification in this sense is fundamental to the scientific method.In logic,...
becomes implicit: universal quantifiers
Universal quantification
In predicate logic, universal quantification formalizes the notion that something is true for everything, or every relevant thing....
on variables (X, Y, …) are simply omitted as understood, while existentially-quantified
Existential quantification
In predicate logic, an existential quantification is the predication of a property or relation to at least one member of the domain. It is denoted by the logical operator symbol ∃ , which is called the existential quantifier...
variables are replaced by Skolem functions.
-

-
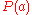
- Therefore,
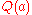
So the question is, how does the resolution technique derive the last clause from the first two? The rule is simple:
- Find two clauses containing the same predicate, where it is negated in one clause but not in the other.
- Perform a unification on the two predicates. (If the unification fails, you made a bad choice of predicates. Go back to the previous step and try again.)
- If any unbound variables which were bound in the unified predicates also occur in other predicates in the two clauses, replace them with their bound values (terms) there as well.
- Discard the unified predicates, and combine the remaining ones from the two clauses into a new clause, also joined by the "∨" operator.
To apply this rule to the above example, we find the predicate P occurs in negated form
- ¬P(X)
in the first clause, and in non-negated form
- P(a)
in the second clause. X is an unbound variable, while a is a bound value (term). Unifying the two produces the substitution
- X a
Discarding the unified predicates, and applying this substitution to the remaining predicates (just Q(X), in this case), produces the conclusion:
- Q(a)
For another example, consider the syllogistic form
- All Cretans are islanders.
- All islanders are liars.
- Therefore all Cretans are liars.
Or more generally,
- ∀X P(X) → Q(X)
- ∀X Q(X) → R(X)
- Therefore, ∀X P(X) → R(X)
In CNF, the antecedents become:
- ¬P(X) ∨ Q(X)
- ¬Q(Y) ∨ R(Y)
(Note that the variable in the second clause was renamed to make it clear that variables in different clauses are distinct.)
Now, unifying Q(X) in the first clause with ¬Q(Y) in the second clause means that X and Y become the same variable anyway. Substituting this into the remaining clauses and combining them gives the conclusion:
- ¬P(X) ∨ R(X)
The resolution rule, as defined by Robinson, also incorporated factoring, which unifies two literals in the same clause, before or during the application of resolution as defined above. The resulting inference rule is refutation complete, in that a set of clauses is unsatisfiable if and only if there exists a derivation of the empty clause using resolution alone.
Implementations
- CarineCarine theorem proverCARINE is a first-order classical logic automated theorem prover.CARINE is a resolution based theorem prover initially built for the study of the enhancement effects of the strategies delayed clause-construction and attribute sequences in a depth-first search based algorithm [Haroun 2005]...
- GandalfGandalf theorem proverGandalf is a first-order automated theorem prover applied to several domain-specifictasks such as Semantic web. It has also participated in The CADE ATP System Competition and had impressive results in that competition. It is programmed in the Scheme programming language which is then compiled to...
- OtterOtter theorem proverOtter is an automated theorem prover developed by William McCune at Argonne National Laboratory in Illinois. Otter was the first widely distributed, high-performance theorem prover for first-order logic, and it pioneered a number of important implementation techniques...
- Prover9
- SNARKSNARK theorem proverSNARK, , is a theorem prover for multi-sorted first-order logic intended for applications in artificial intelligence and software engineering....
- SPASSSPASS theorem proverSPASS is an automated theorem prover for first-order logic with equality developed at the Max Planck Institute for Computer Science and using the superposition calculus....
- VampireVampire theorem proverVampire is an automatic theorem prover for first-order classical logic developed in the Computer Science Department of the University of Manchester byProf. Andrei Voronkov together with Kryštof Hoder and previously with Dr. Alexandre Riazanov...
See also
- Conjunctive normal formConjunctive normal formIn Boolean logic, a formula is in conjunctive normal form if it is a conjunction of clauses, where a clause is a disjunction of literals.As a normal form, it is useful in automated theorem proving...
- Consensus theoremConsensus theoremIn Boolean algebra, the consensus theorem is a simplification of the following terms:Proof for this theorem is: LHS = xy + x'z + yz = xy + x'z + xyz + x'yz...
- Inverse resolutionInverse resolutionInverse resolution is an inductive reasoning technique that involves inverting the resolution operator.-References:...
- Logic ProgrammingLogic programmingLogic programming is, in its broadest sense, the use of mathematical logic for computer programming. In this view of logic programming, which can be traced at least as far back as John McCarthy's [1958] advice-taker proposal, logic is used as a purely declarative representation language, and a...
- Inductive Logic ProgrammingInductive logic programmingInductive logic programming is a subfield of machine learning which uses logic programming as a uniform representation for examples, background knowledge and hypotheses...
- SLD resolutionSLD resolutionSLD resolution is the basic inference rule used in logic programming. It is a refinement of resolution, which is both sound and refutation complete for Horn clauses.-The SLD inference rule:...
- Method of analytic tableauxMethod of analytic tableauxIn proof theory, the semantic tableau is a decision procedure for sentential and related logics, and a proof procedure for formulas of first-order logic. The tableau method can also determine the satisfiability of finite sets of formulas of various logics. It is the most popular proof procedure...

