
Literal (mathematical logic)
Encyclopedia
In mathematical logic
, a literal is an atomic formula
(atom) or its negation
.
The definition mostly appears in proof theory
(of classical logic
), e.g. in conjunctive normal form
and the method of resolution
.
Literals can be divided into two types:
For a literal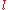 , the complementary literal is a literal corresponding to the negation of
, the complementary literal is a literal corresponding to the negation of 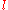 ,
,
we can write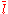 to denote the complementary literal of
to denote the complementary literal of 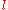 . More precisely, if
. More precisely, if  then
then 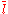 is
is  and if
and if 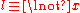 then
then 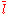 is
is  .
.
In the context of a formula in the conjunctive normal form
, a literal is pure if the literal's complement does not appear in the formula.
a literal is simply a propositional variable
or its negation.
In predicate calculus a literal is an atomic formula
or its negation, where an atomic formula is a predicate symbol applied to some terms
, with the terms recursively defined
with the terms recursively defined
starting from constant symbols, variable symbols, and function
symbols. For example,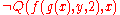 is a negative literal with the constant symbol 2, the variable symbols x, y, the function symbols f, g, and the predicate symbol Q.
is a negative literal with the constant symbol 2, the variable symbols x, y, the function symbols f, g, and the predicate symbol Q.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, a literal is an atomic formula
Atomic formula
In mathematical logic, an atomic formula is a formula with no deeper propositional structure, that is, a formula that contains no logical connectives or equivalently a formula that has no strict subformulas. Atoms are thus the simplest well-formed formulas of the logic...
(atom) or its negation
Negation
In logic and mathematics, negation, also called logical complement, is an operation on propositions, truth values, or semantic values more generally. Intuitively, the negation of a proposition is true when that proposition is false, and vice versa. In classical logic negation is normally identified...
.
The definition mostly appears in proof theory
Proof theory
Proof theory is a branch of mathematical logic that represents proofs as formal mathematical objects, facilitating their analysis by mathematical techniques. Proofs are typically presented as inductively-defined data structures such as plain lists, boxed lists, or trees, which are constructed...
(of classical logic
Classical logic
Classical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...
), e.g. in conjunctive normal form
Conjunctive normal form
In Boolean logic, a formula is in conjunctive normal form if it is a conjunction of clauses, where a clause is a disjunction of literals.As a normal form, it is useful in automated theorem proving...
and the method of resolution
Resolution (logic)
In mathematical logic and automated theorem proving, resolution is a rule of inference leading to a refutation theorem-proving technique for sentences in propositional logic and first-order logic...
.
Literals can be divided into two types:
- A positive literal is just an atom.
- A negative literal is the negation of an atom.
For a literal
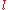 , the complementary literal is a literal corresponding to the negation of
, the complementary literal is a literal corresponding to the negation of 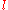 ,
,we can write
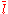 to denote the complementary literal of
to denote the complementary literal of 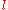 . More precisely, if
. More precisely, if  then
then 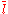 is
is  and if
and if 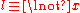 then
then 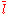 is
is  .
.In the context of a formula in the conjunctive normal form
Conjunctive normal form
In Boolean logic, a formula is in conjunctive normal form if it is a conjunction of clauses, where a clause is a disjunction of literals.As a normal form, it is useful in automated theorem proving...
, a literal is pure if the literal's complement does not appear in the formula.
Examples
In propositional calculusPropositional calculus
In mathematical logic, a propositional calculus or logic is a formal system in which formulas of a formal language may be interpreted as representing propositions. A system of inference rules and axioms allows certain formulas to be derived, called theorems; which may be interpreted as true...
a literal is simply a propositional variable
Propositional variable
In mathematical logic, a propositional variable is a variable which can either be true or false...
or its negation.
In predicate calculus a literal is an atomic formula
Atomic formula
In mathematical logic, an atomic formula is a formula with no deeper propositional structure, that is, a formula that contains no logical connectives or equivalently a formula that has no strict subformulas. Atoms are thus the simplest well-formed formulas of the logic...
or its negation, where an atomic formula is a predicate symbol applied to some terms
Term (logic)
In mathematical logic, universal algebra, and rewriting systems, terms are expressions which can be obtained from constant symbols, variables and function symbols...
,
 with the terms recursively defined
with the terms recursively definedRecursive definition
In mathematical logic and computer science, a recursive definition is used to define an object in terms of itself ....
starting from constant symbols, variable symbols, and function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
symbols. For example,
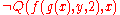 is a negative literal with the constant symbol 2, the variable symbols x, y, the function symbols f, g, and the predicate symbol Q.
is a negative literal with the constant symbol 2, the variable symbols x, y, the function symbols f, g, and the predicate symbol Q.

