Proof theory
Encyclopedia
Proof theory is a branch of mathematical logic
that represents proof
s as formal mathematical object
s, facilitating their analysis by mathematical techniques. Proofs are typically presented as inductively-defined data structures such as plain lists, boxed lists, or trees, which are constructed according to the axiom
s and rules of inference
of the logical system. As such, proof theory is syntactic
in nature, in contrast to model theory
, which is semantic in nature. Together with model theory
, axiomatic set theory, and recursion theory
, proof theory is one of the so-called four pillars of the foundations of mathematics
.
Proof theory is important in philosophical logic
, where the primary interest is in the idea of a proof-theoretic semantics
, an idea which depends upon technical ideas in structural proof theory
to be feasible.
, Giuseppe Peano
, Bertrand Russell
, and Richard Dedekind
, the story of modern proof theory is often seen as being established by David Hilbert
, who initiated what is called Hilbert's program
in the foundations of mathematics
. Kurt Gödel
's seminal work on proof theory first advanced, then refuted this program: his completeness theorem
initially seemed to bode well for Hilbert's aim of reducing all mathematics to a finitist formal system; then his incompleteness theorems showed that this is unattainable. All of this work was carried out with the proof calculi called the Hilbert systems.
In parallel, the foundations of structural proof theory
were being founded. Jan Łukasiewicz suggested in 1926 that one could improve on Hilbert systems as a basis for the axiomatic presentation of logic if one allowed the drawing of conclusions from assumptions in the inference rules of the logic. In response to this Stanisław Jaśkowski (1929) and Gerhard Gentzen
(1934) independently provided such systems, called calculi of natural deduction
, with Gentzen's approach introducing the idea of symmetry between the grounds for asserting propositions, expressed in introduction rules, and the consequences of accepting propositions in the elimination rules, an idea that has proved very important in proof theory. Gentzen (1934) further introduced the idea of the sequent calculus
, a calculus advanced in a similar spirit that better expressed the duality of the logical connectives, and went on to make fundamental advances in the formalisation of intuitionistic logic, and provide the first combinatorial proof
of the consistency of Peano arithmetic. Together, the presentation of natural deduction and the sequent calculus introduced the fundamental idea of analytic proof
to proof theory,
Formal proofs are constructed with the help of computers in interactive theorem proving
.
Significantly, these proofs can be checked automatically, also by computer. (Checking formal proofs is usually simple, whereas finding proofs (automated theorem proving
) is generally hard.) An informal proof in the mathematics literature, by contrast, requires weeks of peer review
to be checked, and may still contain errors.
Each of these can give a complete and axiomatic formalization of propositional or predicate logic
of either the classical
or intuitionistic
flavour, almost any modal logic
, and many substructural logic
s, such as relevance logic
or
linear logic
. Indeed it is unusual to find a logic that resists being represented in one of these calculi.
. The central idea of this program was that if we could give finitary proofs of consistency for all the sophisticated formal theories needed by mathematicians, then we could ground these theories by means of a metamathematical argument, which shows that all of their purely universal assertions (more technically their provable
sentences
) are finitarily true; once so grounded we do not care about the non-finitary meaning of their existential theorems, regarding these as pseudo-meaningful stipulations of the existence of ideal entities.
The failure of the program was induced by Kurt Gödel
's incompleteness theorems
, which showed that any ω-consistent theory that is sufficiently strong to express certain simple arithmetic truths, cannot prove its own consistency, which on Gödel's formulation is a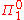
sentence.
Much investigation has been carried out on this topic since, which has in particular led to:
See also Mathematical logic
. The notion of analytic proof was introduced by Gentzen for the sequent calculus; there the analytic proofs are those that are cut-free
. His natural deduction calculus also supports a notion of analytic proof, as shown by Dag Prawitz
. The definition is slightly more complex: we say the analytic proofs are the normal forms, which are related to the notion of normal form in term rewriting. More exotic proof calculi such as Jean-Yves Girard
's proof net
s also support a notion of analytic proof.
Structural proof theory is connected to type theory
by means of the Curry-Howard correspondence, which observes a structural analogy between the process of normalisation in the natural deduction calculus and beta reduction in the typed lambda calculus
. This provides the foundation for the intuitionistic type theory
developed by Per Martin-Löf
, and is often extended to a three way correspondence, the third leg of which are the cartesian closed categories
.
, type-logical grammar, categorial grammar
and Montague grammar
apply formalisms based on structural proof theory to give a formal natural language semantics
.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
that represents proof
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
s as formal mathematical object
Mathematical object
In mathematics and the philosophy of mathematics, a mathematical object is an abstract object arising in mathematics.Commonly encountered mathematical objects include numbers, permutations, partitions, matrices, sets, functions, and relations...
s, facilitating their analysis by mathematical techniques. Proofs are typically presented as inductively-defined data structures such as plain lists, boxed lists, or trees, which are constructed according to the axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s and rules of inference
Rule of inference
In logic, a rule of inference, inference rule, or transformation rule is the act of drawing a conclusion based on the form of premises interpreted as a function which takes premises, analyses their syntax, and returns a conclusion...
of the logical system. As such, proof theory is syntactic
Syntax (logic)
In logic, syntax is anything having to do with formal languages or formal systems without regard to any interpretation or meaning given to them...
in nature, in contrast to model theory
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, which is semantic in nature. Together with model theory
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, axiomatic set theory, and recursion theory
Recursion theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
, proof theory is one of the so-called four pillars of the foundations of mathematics
Foundations of mathematics
Foundations of mathematics is a term sometimes used for certain fields of mathematics, such as mathematical logic, axiomatic set theory, proof theory, model theory, type theory and recursion theory...
.
Proof theory is important in philosophical logic
Philosophical logic
Philosophical logic is a term introduced by Bertrand Russell to represent his idea that the workings of natural language and thought can only be adequately represented by an artificial language; essentially it was his formalization program for the natural language...
, where the primary interest is in the idea of a proof-theoretic semantics
Proof-theoretic semantics
Proof-theoretic semantics is an approach to the semantics of logic that attempts to locate the meaning of propositions and logical connectives not in terms of interpretations, as in Tarskian approaches to semantics, but in the role that the proposition or logical connective plays within the system...
, an idea which depends upon technical ideas in structural proof theory
Structural proof theory
In mathematical logic, structural proof theory is the subdiscipline of proof theory that studies proof calculi that support a notion of analytic proof.-Analytic proof:...
to be feasible.
History
Although the formalisation of logic was much advanced by the work of such figures as Gottlob FregeGottlob Frege
Friedrich Ludwig Gottlob Frege was a German mathematician, logician and philosopher. He is considered to be one of the founders of modern logic, and made major contributions to the foundations of mathematics. He is generally considered to be the father of analytic philosophy, for his writings on...
, Giuseppe Peano
Giuseppe Peano
Giuseppe Peano was an Italian mathematician, whose work was of philosophical value. The author of over 200 books and papers, he was a founder of mathematical logic and set theory, to which he contributed much notation. The standard axiomatization of the natural numbers is named the Peano axioms in...
, Bertrand Russell
Bertrand Russell
Bertrand Arthur William Russell, 3rd Earl Russell, OM, FRS was a British philosopher, logician, mathematician, historian, and social critic. At various points in his life he considered himself a liberal, a socialist, and a pacifist, but he also admitted that he had never been any of these things...
, and Richard Dedekind
Richard Dedekind
Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...
, the story of modern proof theory is often seen as being established by David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
, who initiated what is called Hilbert's program
Hilbert's program
In mathematics, Hilbert's program, formulated by German mathematician David Hilbert, was a proposed solution to the foundational crisis of mathematics, when early attempts to clarify the foundations of mathematics were found to suffer from paradoxes and inconsistencies...
in the foundations of mathematics
Foundations of mathematics
Foundations of mathematics is a term sometimes used for certain fields of mathematics, such as mathematical logic, axiomatic set theory, proof theory, model theory, type theory and recursion theory...
. Kurt Gödel
Kurt Gödel
Kurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the...
's seminal work on proof theory first advanced, then refuted this program: his completeness theorem
Gödel's completeness theorem
Gödel's completeness theorem is a fundamental theorem in mathematical logic that establishes a correspondence between semantic truth and syntactic provability in first-order logic. It was first proved by Kurt Gödel in 1929....
initially seemed to bode well for Hilbert's aim of reducing all mathematics to a finitist formal system; then his incompleteness theorems showed that this is unattainable. All of this work was carried out with the proof calculi called the Hilbert systems.
In parallel, the foundations of structural proof theory
Structural proof theory
In mathematical logic, structural proof theory is the subdiscipline of proof theory that studies proof calculi that support a notion of analytic proof.-Analytic proof:...
were being founded. Jan Łukasiewicz suggested in 1926 that one could improve on Hilbert systems as a basis for the axiomatic presentation of logic if one allowed the drawing of conclusions from assumptions in the inference rules of the logic. In response to this Stanisław Jaśkowski (1929) and Gerhard Gentzen
Gerhard Gentzen
Gerhard Karl Erich Gentzen was a German mathematician and logician. He had his major contributions in the foundations of mathematics, proof theory, especially on natural deduction and sequent calculus...
(1934) independently provided such systems, called calculi of natural deduction
Natural deduction
In logic and proof theory, natural deduction is a kind of proof calculus in which logical reasoning is expressed by inference rules closely related to the "natural" way of reasoning...
, with Gentzen's approach introducing the idea of symmetry between the grounds for asserting propositions, expressed in introduction rules, and the consequences of accepting propositions in the elimination rules, an idea that has proved very important in proof theory. Gentzen (1934) further introduced the idea of the sequent calculus
Sequent calculus
In proof theory and mathematical logic, sequent calculus is a family of formal systems sharing a certain style of inference and certain formal properties. The first sequent calculi, systems LK and LJ, were introduced by Gerhard Gentzen in 1934 as a tool for studying natural deduction in...
, a calculus advanced in a similar spirit that better expressed the duality of the logical connectives, and went on to make fundamental advances in the formalisation of intuitionistic logic, and provide the first combinatorial proof
Combinatorial proof
In mathematics, the term combinatorial proof is often used to mean either of two types of proof of an identity in enumerative combinatorics that either states that two sets of combinatorial configurations, depending on one or more parameters, have the same number of elements , or gives a formula...
of the consistency of Peano arithmetic. Together, the presentation of natural deduction and the sequent calculus introduced the fundamental idea of analytic proof
Analytic proof
In mathematical analysis, an analytical proof is a proof of a theorem in analysis that only makes use of methods from analysis, and which does not make use of results from geometry...
to proof theory,
Formal and informal proof
The informal proofs of everyday mathematical practice are unlike the formal proofs of proof theory. They are rather like high-level sketches that would allow an expert to reconstruct a formal proof at least in principle, given enough time and patience. For most mathematicians, writing a fully formal proof is too pedantic and long-winded to be in common use.Formal proofs are constructed with the help of computers in interactive theorem proving
Interactive theorem proving
In computer science and mathematical logic, a proof assistant or interactive theorem prover is a software tool to assist with the development of formal proofs by man-machine collaboration...
.
Significantly, these proofs can be checked automatically, also by computer. (Checking formal proofs is usually simple, whereas finding proofs (automated theorem proving
Automated theorem proving
Automated theorem proving or automated deduction, currently the most well-developed subfield of automated reasoning , is the proving of mathematical theorems by a computer program.- Decidability of the problem :...
) is generally hard.) An informal proof in the mathematics literature, by contrast, requires weeks of peer review
Peer review
Peer review is a process of self-regulation by a profession or a process of evaluation involving qualified individuals within the relevant field. Peer review methods are employed to maintain standards, improve performance and provide credibility...
to be checked, and may still contain errors.
Kinds of proof calculi
The three most well-known styles of proof calculi are:- The Hilbert calculi
- The natural deduction calculi
- The sequent calculiSequent calculusIn proof theory and mathematical logic, sequent calculus is a family of formal systems sharing a certain style of inference and certain formal properties. The first sequent calculi, systems LK and LJ, were introduced by Gerhard Gentzen in 1934 as a tool for studying natural deduction in...
Each of these can give a complete and axiomatic formalization of propositional or predicate logic
Predicate logic
In mathematical logic, predicate logic is the generic term for symbolic formal systems like first-order logic, second-order logic, many-sorted logic or infinitary logic. This formal system is distinguished from other systems in that its formulae contain variables which can be quantified...
of either the classical
Classical logic
Classical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...
or intuitionistic
Intuitionistic logic
Intuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
flavour, almost any modal logic
Modal logic
Modal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
, and many substructural logic
Substructural logic
In logic, a substructural logic is a logic lacking one of the usual structural rules , such as weakening, contraction or associativity...
s, such as relevance logic
Relevance logic
Relevance logic, also called relevant logic, is a kind of non-classical logic requiring the antecedent and consequent of implications be relevantly related. They may be viewed as a family of substructural or modal logics...
or
linear logic
Linear logic
Linear logic is a substructural logic proposed by Jean-Yves Girard as a refinement of classical and intuitionistic logic, joining the dualities of the former with many of the constructive properties of the latter...
. Indeed it is unusual to find a logic that resists being represented in one of these calculi.
Consistency proofs
As previously mentioned, the spur for the mathematical investigation of proofs in formal theories was Hilbert's programHilbert's program
In mathematics, Hilbert's program, formulated by German mathematician David Hilbert, was a proposed solution to the foundational crisis of mathematics, when early attempts to clarify the foundations of mathematics were found to suffer from paradoxes and inconsistencies...
. The central idea of this program was that if we could give finitary proofs of consistency for all the sophisticated formal theories needed by mathematicians, then we could ground these theories by means of a metamathematical argument, which shows that all of their purely universal assertions (more technically their provable
sentencesArithmetical hierarchy
In mathematical logic, the arithmetical hierarchy, arithmetic hierarchy or Kleene-Mostowski hierarchy classifies certain sets based on the complexity of formulas that define them...
) are finitarily true; once so grounded we do not care about the non-finitary meaning of their existential theorems, regarding these as pseudo-meaningful stipulations of the existence of ideal entities.
The failure of the program was induced by Kurt Gödel
Kurt Gödel
Kurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the...
's incompleteness theorems
Gödel's incompleteness theorems
Gödel's incompleteness theorems are two theorems of mathematical logic that establish inherent limitations of all but the most trivial axiomatic systems capable of doing arithmetic. The theorems, proven by Kurt Gödel in 1931, are important both in mathematical logic and in the philosophy of...
, which showed that any ω-consistent theory that is sufficiently strong to express certain simple arithmetic truths, cannot prove its own consistency, which on Gödel's formulation is a
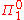sentence.Much investigation has been carried out on this topic since, which has in particular led to:
- Refinement of Gödel's result, particularly J. Barkley Rosser's refinement, weakening the above requirement of ω-consistency to simple consistency;
- Axiomatisation of the core of Gödel's result in terms of a modal language, provability logicProvability logicProvability logic is a modal logic, in which the box operator is interpreted as 'it is provable that'. The point is to capture the notion of a proof predicate of a reasonably rich formal theory, such as Peano arithmetic....
; - Transfinite iteration of theories, due to Alan TuringAlan TuringAlan Mathison Turing, OBE, FRS , was an English mathematician, logician, cryptanalyst, and computer scientist. He was highly influential in the development of computer science, providing a formalisation of the concepts of "algorithm" and "computation" with the Turing machine, which played a...
and Solomon FefermanSolomon FefermanSolomon Feferman is an American philosopher and mathematician with major works in mathematical logic.He was born in New York City, New York, and received his Ph.D. in 1957 from the University of California, Berkeley under Alfred Tarski...
; - The recent discovery of self-verifying theoriesSelf-verifying theoriesSelf-verifying theories are consistent first-order systems of arithmetic much weaker than Peano arithmetic that are capable of proving their own consistency. Dan Willard was the first to investigate their properties, and he has described a family of such systems...
, systems strong enough to talk about themselves, but too weak to carry out the diagonal argument that is the key to Gödel's unprovability argument.
See also Mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
Structural proof theory
Structural proof theory is the subdiscipline of proof theory that studies proof calculi that support a notion of analytic proofAnalytic proof
In mathematical analysis, an analytical proof is a proof of a theorem in analysis that only makes use of methods from analysis, and which does not make use of results from geometry...
. The notion of analytic proof was introduced by Gentzen for the sequent calculus; there the analytic proofs are those that are cut-free
Cut-elimination theorem
The cut-elimination theorem is the central result establishing the significance of the sequent calculus. It was originally proved by Gerhard Gentzen 1934 in his landmark paper "Investigations in Logical Deduction" for the systems LJ and LK formalising intuitionistic and classical logic respectively...
. His natural deduction calculus also supports a notion of analytic proof, as shown by Dag Prawitz
Dag Prawitz
Dag Prawitz is a Swedish philosopher and logician. He is best known for his work on proof theory and the foundations of natural deduction....
. The definition is slightly more complex: we say the analytic proofs are the normal forms, which are related to the notion of normal form in term rewriting. More exotic proof calculi such as Jean-Yves Girard
Jean-Yves Girard
Jean-Yves Girard is a French logician working in proof theory. His contributions include a proof of strong normalization in a system of second-order logic called system F; the invention of linear logic; the geometry of interaction; and ludics...
's proof net
Proof net
In proof theory, proof nets are a geometrical method of representing proofs thateliminates two forms of bureaucracy that differentiates proofs: irrelevant syntactical features of regular proof calculi such as the natural deduction calculus and the sequent calculus, and the order of rules applied...
s also support a notion of analytic proof.
Structural proof theory is connected to type theory
Type theory
In mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general...
by means of the Curry-Howard correspondence, which observes a structural analogy between the process of normalisation in the natural deduction calculus and beta reduction in the typed lambda calculus
Typed lambda calculus
A typed lambda calculus is a typed formalism that uses the lambda-symbol to denote anonymous function abstraction. In this context, types are usually objects of a syntactic nature that are assigned to lambda terms; the exact nature of a type depends on the calculus considered...
. This provides the foundation for the intuitionistic type theory
Intuitionistic type theory
Intuitionistic type theory, or constructive type theory, or Martin-Löf type theory or just Type Theory is a logical system and a set theory based on the principles of mathematical constructivism. Intuitionistic type theory was introduced by Per Martin-Löf, a Swedish mathematician and philosopher,...
developed by Per Martin-Löf
Per Martin-Löf
Per Erik Rutger Martin-Löf is a Swedish logician, philosopher, and mathematical statistician. He is internationally renowned for his work on the foundations of probability, statistics, mathematical logic, and computer science. Since the late 1970s, Martin-Löf's publications have been mainly in...
, and is often extended to a three way correspondence, the third leg of which are the cartesian closed categories
Cartesian closed category
In category theory, a category is cartesian closed if, roughly speaking, any morphism defined on a product of two objects can be naturally identified with a morphism defined on one of the factors. These categories are particularly important in mathematical logic and the theory of programming, in...
.
Proof-theoretic semantics
In linguisticsLinguistics
Linguistics is the scientific study of human language. Linguistics can be broadly broken into three categories or subfields of study: language form, language meaning, and language in context....
, type-logical grammar, categorial grammar
Categorial grammar
Categorial grammar is a term used for a family of formalisms in natural language syntax motivated by the principle of compositionality and organized according to the view that syntactic constituents should generally combine as functions or according to a function-argument relationship...
and Montague grammar
Montague grammar
Montague grammar is an approach to natural language semantics, named after American logician Richard Montague. The Montague grammar is based on formal logic, especially higher order predicate logic and lambda calculus, and makes use of the notions of intensional logic, via Kripke models...
apply formalisms based on structural proof theory to give a formal natural language semantics
Natural Language Semantics
Natural Language Semantics: An International Journal of Semantics and Its Interfaces in Grammar is a leading international peer-reviewed semantics journal published by Springer Netherlands . It is devoted to semantics and its interfaces in grammar, especially in syntax...
.
Tableau systems
Analytic tableaux apply the central idea of analytic proof from structural proof theory to provide decision procedures and semi-decision procedures for a wide range of logics.Ordinal analysis
Ordinal analysis is a powerful technique for providing combinatorial consistency proofs for theories formalising arithmetic and analysis.Logics from proof analysis
Several important logics have come from insights into logical structure arising in structural proof theory.See also
- Proof techniques
- Intermediate logics
- Proof (truth)Proof (truth)A proof is sufficient evidence or argument for the truth of a proposition.The concept arises in a variety of areas, with both the nature of the evidence or justification and the criteria for sufficiency being area-dependent...
- Model theoryModel theoryIn mathematics, model theory is the study of mathematical structures using tools from mathematical logic....